Čtvrtý rozměr


Čtvrtý rozměr nebo čtyřrozměrný prostor (4D) je abstraktní pojem, vzniklý zobecněním pravidel třírozměrného prostoru. Matematici i filozofové jej studují už skoro dvě stě let (např. Möbius, Riemann), protože je zaujal a nabízí zajímavé náhledy na matematiku a příbuzné obory.
Algebraicky vzniká tak, že se pravidla vektorů a souřadnicové geometrie uplatní na prostor o čtyřech rozměrech. Čtyřrozměrný vektor (uspořádanou čtveřici čísel) lze chápat jako umístění ve čtyřrozměrném prostoru. To je euklidovský prostor, který má metriku i normu, takže se všemi rozměry lze zacházet stejně: přidaný rozměr se nijak neliší od ostatních tří.
Ve 20. století byl vyvinut pojem časoprostoru, který spojuje prostor a čas, jenže s odlišnou metrikou, takže s rozměrem času se zachází jinak než se třemi rozměry prostorovými. Časoprostor tedy není euklidovský prostor, ale Minkowského prostor.
Historie
Možnost prostorů s více než třemi rozměry byla poprvé zkoumána matematiky v 19. století. V roce 1827 si Möbius uvědomil, že čtvrtá dimenze by umožnila, aby třírozměrný objekt otáčením přešel do svého zrcadlového obrazu. Kolem roku 1853 objevil Schläfli mnoho polytopů ve vyšších dimenzích, práce však vyšla až po jeho smrti. Vyšší rozměry brzy podpořil habilitační spis Bernharda Riemanna Über die Hypothesen welche der Geometrie zu Grunde liegen („O hypotézách, na nichž je založena geometrie“), kde „bod“ považoval za jakoukoli posloupnost souřadnic . Možnost geometrie ve vyšších dimenzích, včetně zejména čtvrtého rozměru, byla tímto podložena.
Čtvrtou dimenzi proslavil Charles Howard Hinton esejem What is the Fourth Dimension? (Co je čtvrtá dimenze?), zveřejněným v roce 1880 v časopise Dublinské univerzity. Ve své knize A New Era of Thought (Nová éra myšlení) představil tesseract (ekvivalent krychle ve čtvrtém rozměru) a ana a kata (dva nové směry) a v knize Fourth Dimension (Čtvrtá dimenze) zavedl postup, jak znázorňovat čtvrtý rozměr pomocí krychlí.
Vlastnosti čtyřrozměrného prostoru

Pro pozorovatele zvyklého na třírozměrný prostor přináší čtvrtý rozměr některé zvláštnosti:
- Dvě roviny mohou mít společný i právě jeden bod. V třírozměrném světě průsečík dvou různých rovin buď neexistuje (rovnoběžné roviny), nebo je průsečíkem přímka nebo rovina (pokud jsou totožné).
- Otáčivé dveře (turniket) v každém okamžiku uzavírají nějaký prostor, a přece jimi lze v čase (jako ve „čtvrtém rozměru“) projít. Křídla turniketu totiž vytvářejí jakousi pohyblivou komůrku, do níž lze vstoupit, pak se při dalším otáčení uzavře a opět otevře na druhé straně. Nicméně pro statický pohled ve třech rozměrech oba prostory v každém okamžiku oddělují.[1]
Odkazy
Reference
V tomto článku byl použit překlad textu z článku Fourth dimension na anglické Wikipedii.
- ↑ R. Ruyer, Paradoxy vědomí. Praha: PedF UK 1994, str. 78n.
Související články
Externí odkazy
- Model čtyřrozměrné krychle - tvořený několika sousedícími krychlemi, jež se zdánlivě prostupují
- 4D analogie krychle - popis konstrukce a vlastností teseraktu, včetně čtyřrozměrné Rubikovy kostky (3x3x3x3)
- Zajímavé video o čtvrtém rozměru
- (anglicky)
- "Dimensions" – různé způsoby vizualizace čtyřrozměrných předmětů
- Článek Science News, shrnující videa "Dimensions" Archivováno 29. 9. 2012 na Wayback Machine.
Média použitá na této stránce
Created by Jason Hise with Maya and Macromedia Fireworks. A 3D projection of an 8-cell performing a simple rotation about a plane which bisects the figure from front-left to back-right and top to bottom.
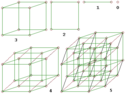
Autor: de:Benutzer:Karl Bednarik, Licence: CC BY-SA 3.0
Parallelprojektionen der 0- bis 5-dimensionalen Würfelanaloga
Průsečík dvou rovin alfa a beta ve čtyřrozměrném prostoru. Čtvrtý rozměr je rozlišen barvou, od 0 (bílá) do 1 (černá). (V třírozměrném světě existuje pouze bílá barva.) Bod B leží v rovině alfa, bod C leží v rovině beta, tyto dva body se liší pouze ve čtvrté souřadnici. Průsečíkem rovin je bod se souřadnicemi [0; 0; 0; 0].