AVL-strom


AVL strom je datová struktura pro uchovávání údajů a jejich vyhledávání. Pracuje v logaritmicky omezeném čase. Jedná se o samovyvažující se binární vyhledávací strom.
Jméno stromu pochází z iniciál jeho objevitelů. G. M. Adeľson-Velskij a Je. M. Landis popsali tuto strukturu v roce 1962 v článku An algorithm for the organization of information. Dokázali, že AVL-strom bude maximálně o 45 % vyšší než dokonale vyvážený strom, složený ze stejných vrcholů. Pokud v(n) je výška AVL-stromu s n uzly, potom platí
log(n+1) ≤ v(n) ≤ 1.4404 log(n+2) − 0.328.
Vlastnosti vrcholů AVL stromu
- Vrchol má maximálně dva následníky (je to binární strom).
- V levém podstromu vrcholu jsou pouze vrcholy s menší hodnotou klíče (je to binární vyhledávací strom).
- V pravém podstromu vrcholu jsou pouze vrcholy s větší hodnotou klíče (je to binární vyhledávací strom).
- Délka nejdelší větve levého a pravého podstromu každého uzlu se liší nejvýše o 1 (vyvážení AVL stromu).
Vlastnosti AVL stromu
Hlavní vlastností AVL stromu je, že definice nedovoluje, aby strom zdegeneroval, tj. zajišťuje vyváženost stromu. Pokud označíme i výšku stromu reprezentujícího množinu o velikosti n, platí následující:
,
kde je i-té Fibonacciho číslo. Z toho plyne, že výška stromu je úměrná logaritmu velikosti reprezentované množiny.
Operace
Na AVL stromech je možno v čase provádět následující operace:
- vyhledání uzlu
- vložení uzlu
- zrušení uzlu
Vyhledání uzlu v AVL stromu
Vyhledávání uzlu v AVL stromu se realizuje stejně jako u binárního vyhledávacího stromu. Tato operace neklade žádné speciální požadavky a nemění strukturu stromu.
Vkládání do AVL stromu
Přidáváme-li nebo rušíme-li vrchol ve vyváženém stromu, může se tento strom stát nevyváženým.
Koeficient vyváženosti i-tého uzlu Bi = | vLi - vRi |, kde vLi je výška levého podstromu i-tého uzlu a vRi je výška pravého podstromu i-tého uzlu. Strom s kořenem i je vyvážený, jestliže Bi ≤ 1. Předpokládejme, že přidáme uzel do levého podstromu. Pokud si označíme K kořen, L levý, P pravý podstrom a vL, vP jejich výšky, pak před přidáním bude platit jedna z následujících možností:
- vL = vP
- Po přidání bude tedy výška levého podstromu o jedničku větší než je výška pravého podstromu, a proto bude vyváženost stromu zachována.
- vL < vP
- Po přidání budou výšky podstromů sobě rovny a kritérium vyváženosti se tedy ještě zlepší.
- vL > vP
- Po přidání bude výška levého podstromu o dvě větší než je výška pravého podstromu a bude kritérium vyváženosti stromu porušeno.
Před vložením hodnoty nejprve zjistíme, zda se daný uzel ve stromu již nenachází. Pokud takový uzel neexistuje, pak přidáme nový stejně jako u binárního vyhledávacího stromu a určíme pro něj koeficient vyváženosti. Potom následuje zkontrolování koeficientu vyváženosti pro každý uzel na cestě směrem ke kořeni stromu. Není-li splněno kritérium vyváženosti, musíme provést vyvažování stromu pomocí cyklické záměny ukazatelů (rotace stromu). Jakmile provedeme první vyvážení stromu, není už nutné pokračovat v procházení stromu až do kořene, protože strom je již vyvážený a koeficienty vyváženosti jsou správně nastaveny.
Při operaci vkládání a rušení je zapotřebí uchovávat o každém uzlu jeho koeficient vyváženosti. Proto je vhodné tento koeficient ukládat do každého vrcholu.
Rušení uzlů z AVL stromu
Rušení uzlů se vykonává stejně jako u binárního vyhledávacího stromu s tím, že pokud dojde k porušení vyváženosti, provede se znovuvyvážení pomocí příslušných jednoduchých či dvojitých rotací. Na rozdíl od vyvažování při vkládání uzlů, při odebírání uzlů se musí projít celá cesta až do kořene stromu a opravit koeficienty vyvážení a případně provést rotace.
Vyvažování AVL stromu
Operace potřebné pro vyvažování jsou realizovány cyklickými záměnami ukazatelů. Můžeme provádět jednoduché RR-rotace (pravá rotace), LL-rotace (levá rotace) nebo dvojité LR-rotace (nejprve levá a potom pravá), RL-rotace (nejprve pravá a potom levá). Při rotaci je nutné aktualizovat koeficient vyváženosti každého rotovaného uzlu.
Na první ukázce je po přidání uzlu do podstromu T3 porušena vyváženost stromu, protože u uzlu X nabývá koeficient vyváženosti hodnoty 2. Jednoduchou LL-rotací získáme opět vyvážený strom. V druhé ukázce je po vložení uzlu do podstromu T1 porušena vyváženost, která je odstraněná RR-rotací.


Přidáním uzlu do podstromu T2 se naruší kritérium vyváženosti kořene X (kritérium se změní na −2). Opětovného vyvážení dosáhneme složitější LR-rotací. Na poslední ukázce vyvažování AVL stromu je kritérium vyváženosti vrcholu X rovno dvěma, a proto je realizovaná dvojitá RL-rotace okolo uzlu X.


Související články
Externí odkazy
 Obrázky, zvuky či videa k tématu AVL-strom na Wikimedia Commons
Obrázky, zvuky či videa k tématu AVL-strom na Wikimedia Commons - Vizualizace AVL stromu
- Aplet na vyvážení binárního stromu: Věra Edelmannová, Iva Henzlová
Média použitá na této stránce
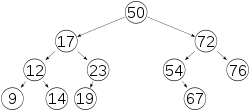
An unbalanced w:binary tree, for comparison with height-balanced AVL trees (as in Image:AVLtreef.svg)
Autor: Gorivero, Licence: CC BY-SA 3.0
Double rotation (left-right) of an en:AVL Tree
Autor: Henning.H, Licence: CC BY-SA 2.0 de
Left rotation (counterclockwise) of an en:AVL Tree, see also Image:AVL-Rightrotation.png.
Autor: Henning.H, Licence: CC BY-SA 2.0 de
Right rotation (clockwise) of an en:AVL Tree, see also Image:AVL-Leftrotation.png.
Autor: Gorivero, Licence: CC BY-SA 3.0
Double rotation (right-left) of an w:en:AVL-tree