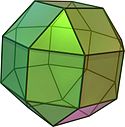
Archimédovské těleso

V geometrii je archimédovské těleso vysoce symetrický, polopravidelný konvexní mnohostěn. Skládá se ze dvou nebo více typů pravidelných mnohoúhelníků, které se setkávají v identických vrcholech. Jsou odlišné od Platonských těles, která se skládají z pouze jednoho typu mnohoúhelníků, setkávajících se v identických vrcholech.

„Identickými vrcholy" se obvykle myslí to, že pro dva libovolné vrcholy musí být izometrie celého tělesa stejná u každého úhlu k ostatním. Někdy je místo toho pouze požadováno, že stěny setkávající se v jednom vrcholu jsou izometricky spojené ke stěnám ostatních.

Hranoly, jejichž symetrické skupiny jsou dihedrální grupy, nejsou obecně považovány za Archimédovská tělesa, a to navzdory výše splněné definici. Všechny mohou být zhotoveny přes Wythoffovou konstrukci z platonských těles.

Původ

Archimédovská tělesa jsou pojmenována podle Archiméda, který o nich napsal ve svých spisech. Během renesance umění matematické „čisté formy" byly nově hledány všechny tyto formy těles. Toto hledání bylo dokončeno v roce 1620 Keplerem.

Klasifikace

Matematika zná třináct archimedovských těles. Další dvě archimédovská tělesa lze získat jako zrcadlové obrazy dvou z výše uvedených třinácti těles. Zde je jejich přehled:

Název (Konfigurace vrcholů)	Transparent	Těleso	Mnohúhelníky	Stěny		Hrany	Vrcholy	Symetrická skupina
komolý čtyřstěn (3.6.6)	(Animace)			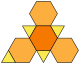8	4 trojúhelníky 4 šestiúhelníky	18	12	Td
kuboktaedr neboli krychloktaedr (3.4.3.4)	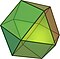(Animace)			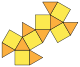14	8 trojúhelníků 6 čtverců	24	12	Oh
komolá krychle nebo osekaný šestistěn (3.8.8)	(Animace)			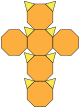14	8 trojúhelníků 6 osmiúhelníků	36	24	Oh
komolý osmistěn (4.6.6)	(Animace)			14	6 čtverců 8 šestiúhelníků	36	24	Oh
rombická krychle nebo malý rombokuboktaedr (3.4.4.4 )	(Animace)			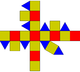26	8 trojúhelníků 18 čtverců	48	24	Oh
komolý krychloktaedr nebo velký rombokuboktaedr (4.6.8)	(Animace)			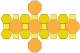26	12 čtverců 8 šestiúhelníků 6 osmiúhelníků	72	48	Oh
přitlačená krychle nebo přitlačený šestistěn nebo otupěný kuboktaedr (2 chiralní formy) (3.3.3.3.4)	(Animace) (Animace)			38	32 trojúhelníků 6 čtverců	60	24	O
ikosidodekaedr (3.5.3.5)	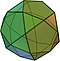(Animace)			32	20 trojúhelníků 12 pětiúhelníků	60	30	Ih
komolý dvanáctistěn (3.10.10)	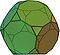(Animace)			32	20 trojúhelníků 12 desetiúhelníků	90	60	Ih
komolý dvacetistěn (5.6.6)	(Animace)			32	12 petiúhelníků 20 šestiúhelníků	90	60	Ih
malý romboikosododekaedr (3.4.5.4)	(Animace)			62	20 trojúhelníků 30 čtverců 12 pětiúhelníků	120	60	Ih
komolý ikosidodekaedr nebo velký rombikosidodekaedron (angl. big rhombicosidodecahedron) (4.6.10)	(Animace)			62	30 čtverců 20 šestiúhelníků 12 desetiúhelníků	180	120	Ih
přitlačený dvanáctistěn nebo otupěný ikosododekaedr (2 chirální formy) (3.3.3.3.5)	(Animace) (Animace)			92	80 trojúhelníků 12 pětiúhelníků	150	60	I

Odkazy

Reference

V tomto článku byl použit překlad textu z článku Archimedean solid na anglické Wikipedii.

Související články

• Platónské těleso
• Kvazikrystal

Externí odkazy

• Obrázky, zvuky či videa k tématu Archimédovské těleso na Wikimedia Commons
• www.telesa.wz.cz Archivováno 10. 6. 2015 na Wayback Machine. – databáze nejrůznějších těles