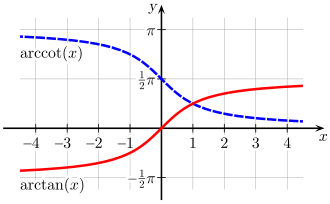
Grafy funkcí arkus tangens a arkus kotangens Arkus tangens je jedna z cyklometrických funkcí , inverzní funkce k funkci tangens . Obvykle se značí arctg x nebo arctan x , v anglické literatuře se taktéž používá atan x či tan−1 x . Její hodnotou je úhel v obloukové míře z intervalu ( − π 2 ; π 2 ) {\displaystyle (-{\tfrac {\pi }{2}};{\tfrac {\pi }{2}})} stupňové míře z intervalu (−90°; 90°), jehož tangens je x . Je to jedna z nejdůležitějších funkcí matematické analýzy .
Definice Funkce arctg x je inverzní funkce k funkci tg x , jejíž definiční obor byl omezen na interval ( − π 2 ; π 2 ) {\displaystyle (-{\tfrac {\pi }{2}};{\tfrac {\pi }{2}})} prostá , takže požadovaná inverzní funkce existuje.
Vlastnosti Funkce y = arctg x {\displaystyle y={\mbox{arctg }}x} obloukové míře je bijekcí mezi množinou reálných čísel R {\displaystyle \mathbb {R} } ( − π 2 ; π 2 ) {\displaystyle (-{\tfrac {\pi }{2}};{\tfrac {\pi }{2}})} interval má stejnou mohutnost jako množina reálných čísel.
Dále má tato funkce následující vlastnosti:
Definiční obor R {\displaystyle \mathbb {R} } Obor hodnot ( − π 2 ; π 2 ) {\displaystyle (-{\tfrac {\pi }{2}};{\tfrac {\pi }{2}})} Omezenost Je omezená Monotonie Je rostoucí prostá Symetrie Je lichá Periodicita Není periodická Limity lim x → − ∞ arctg x = − π 2 {\displaystyle \lim _{x\to -\infty }{\mbox{arctg }}x=-{\tfrac {\pi }{2}}} lim x → + ∞ arctg x = π 2 {\displaystyle \lim _{x\to +\infty }{\mbox{arctg }}x={\tfrac {\pi }{2}}}
lim x → 0 arctg x x = 1 , {\displaystyle \lim \limits _{x\rightarrow 0}{{\mbox{arctg }}x \over x}=1,} okolí nuly je arctg x ≈ x {\displaystyle {\mbox{arctg }}x\approx x}
Inverzní funkce x = tg y {\displaystyle x={\mbox{tg }}y} tangens )Derivace d d x arctg x = 1 1 + x 2 {\displaystyle {\mathrm {d} \over \mathrm {d} x}\,{\mbox{arctg }}x={1 \over {1+x^{2}}}} Integrál ∫ arctg x d x = x arctg x − 1 2 ln ( 1 + x 2 ) + C {\displaystyle \int {\mbox{arctg }}x\;\mathrm {d} x=x\;{\mbox{arctg }}x-{\tfrac {1}{2}}\ln(1+x^{2})+C} Taylorova řada arctg x = x − x 3 3 + x 5 5 − x 7 7 + ⋯ = ∑ n = 0 ∞ ( − 1 ) n x 2 n + 1 2 n + 1 pro x ∈ ⟨ − 1 , 1 ⟩ {\displaystyle \operatorname {arctg} \,x=x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}-{\frac {x^{7}}{7}}+\cdots =\sum _{n=0}^{\infty }{(-1)}^{n}{\frac {x^{2n+1}}{2n+1}}\;{\mbox{ pro }}x\in \langle -1,1\rangle }
Vzorce arctg x = π 2 − arccotg x = arcsin x x 2 + 1 = π 2 − arccos x x 2 + 1 {\displaystyle {\mbox{arctg }}x={\tfrac {\pi }{2}}-{\mbox{arccotg }}x=\arcsin {\frac {x}{\sqrt {x^{2}+1}}}={\tfrac {\pi }{2}}-\arccos {\frac {x}{\sqrt {x^{2}+1}}}}
arctg ( − x ) = − arctg x {\displaystyle {\mbox{arctg }}(-x)=-{\mbox{arctg }}x}
arctg 1 x = { π 2 − arctg x = arccotg x pokud x > 0 − π 2 − arctg x = − π + arccotg x pokud x < 0 {\displaystyle {\mbox{arctg }}{1 \over x}={\begin{cases}{\tfrac {\pi }{2}}-{\mbox{arctg }}x={\mbox{arccotg }}x&{\text{pokud }}x>0\\-{\tfrac {\pi }{2}}-{\mbox{arctg }}x=-\pi +{\mbox{arccotg }}x&{\text{pokud }}x<0\end{cases}}}
1 2 arctg x = arctg x 1 + 1 + x 2 {\displaystyle {\tfrac {1}{2}}\,{\mbox{arctg }}x={\mbox{arctg}}\,{x \over 1+{\sqrt {1+x^{2}}}}}
2 arctg x ≡ arctg 2 x 1 − x 2 ( mod π ) , x ≠ ± 1 {\displaystyle 2\,{\mbox{arctg }}x\equiv {\mbox{arctg}}\,{2x \over 1-x^{2}}{\pmod {\pi }},\quad x\neq \pm 1} [ p 1]
arctg x + arctg y ≡ arctg x + y 1 − x y ( mod π ) , x y ≠ 1 {\displaystyle {\mbox{arctg }}x+{\mbox{arctg }}y\equiv {\mbox{arctg}}\,{x+y \over 1-xy}{\pmod {\pi }},\quad xy\neq 1}
↑ Dosazením x = y do vzorce pro arctg x + arctg y
Obrázky, zvuky či videa k tématu arkus tangens
 Obrázky, zvuky či videa k tématu arkus tangens na Wikimedia Commons
Obrázky, zvuky či videa k tématu arkus tangens na Wikimedia Commons