Grafy funkcí arkus sinus a arkus kosinus Arkus sinus je jedna z cyklometrických funkcí , inverzní funkce k funkci sinus . Obvykle se značí arcsin x {\displaystyle \arcsin x} a s i n x {\displaystyle \operatorname {asin\,} x} sin − 1 x {\displaystyle \sin ^{-1}x} úhel v obloukové míře (radiány) z intervalu ⟨ − π 2 , π 2 ⟩ {\displaystyle \left\langle -{\frac {\pi }{2}},{\frac {\pi }{2}}\right\rangle } sinus je x {\displaystyle x}
Definice Funkce y = arcsin x {\displaystyle y=\arcsin x} x = sin y ( − π 2 ≤ y ≤ π 2 ) {\displaystyle x=\sin y\;\left(-{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}}\right)} x ∈ ⟨ − 1 , 1 ⟩ {\displaystyle x\in \langle -1,1\rangle } [ 1]
Vlastnosti Značení: y = arcsin x {\displaystyle y=\arcsin x\;\;} ( resp. a s i n x , sin − 1 x ) {\displaystyle \qquad \left(\;{\mbox{resp.}}\quad \operatorname {asin\,} x,\quad \sin ^{-1}x\;\right)} [ 2] Definiční obor ⟨ − 1 , 1 ⟩ {\displaystyle \langle -1,1\rangle } Obor hodnot ⟨ − π 2 , π 2 ⟩ {\displaystyle \left\langle -{\frac {\pi }{2}},{\frac {\pi }{2}}\right\rangle } Omezenost Je omezená Monotonie Je ryze rostoucí ⟹ {\displaystyle \quad \Longrightarrow \quad } prostá Symetrie Je lichá sudá Periodicita Není periodická Limity lim x → 0 arcsin x x = 1 {\displaystyle \lim _{x\to 0}{\frac {\arcsin x}{x}}=1\quad } okolí nuly je arcsin x ≈ x {\displaystyle {\mbox{arcsin }}x\approx x} Inverzní funkce x = sin y {\displaystyle x=\sin y} sinus )Derivace ( arcsin x ) ′ = 1 1 − x 2 {\displaystyle (\arcsin x)'={\frac {1}{\sqrt {1-x^{2}}}}} Integrál ∫ arcsin x d x = x arcsin x + 1 − x 2 + C {\displaystyle \int \arcsin x\,\mathrm {d} x=x\arcsin x+{\sqrt {1-x^{2}}}+C} Taylorova řada arcsin x = x + 1 6 x 3 + 3 40 x 5 + 5 112 x 7 + … | x | < 1 {\displaystyle \arcsin x=x+{\frac {1}{6}}x^{3}+{\frac {3}{40}}x^{5}+{\frac {5}{112}}x^{7}+\dots \qquad |x|<1\quad } Významné hodnoty x − 1 − 3 2 − 2 2 − 1 2 0 1 2 2 2 3 2 1 arcsin x − π 2 − π 3 − π 4 − π 6 0 π 6 π 4 π 3 π 2 {\displaystyle {\begin{array}{c|ccc}x&-1&-{\frac {\sqrt {3}}{2}}&-{\frac {\sqrt {2}}{2}}&-{\frac {1}{2}}&0&{\frac {1}{2}}&{\frac {\sqrt {2}}{2}}&{\frac {\sqrt {3}}{2}}&1\\\hline \arcsin x&-{\frac {\pi }{2}}&-{\frac {\pi }{3}}&-{\frac {\pi }{4}}&-{\frac {\pi }{6}}&0&{\frac {\pi }{6}}&{\frac {\pi }{4}}&{\frac {\pi }{3}}&{\frac {\pi }{2}}\end{array}}}
Vzorce arcsin x + arccos x = π 2 arcsin x + arcsin ( − x ) = 0 arcsin x + arcsin y = { arcsin ( x 1 − y 2 + y 1 − x 2 ) , x y ≤ 0 nebo x 2 + y 2 ≤ 1 π − arcsin ( x 1 − y 2 + y 1 − x 2 ) , x > 0 , y > 0 , x 2 + y 2 > 1 − π − arcsin ( x 1 − y 2 + y 1 − x 2 ) , x < 0 , y < 0 , x 2 + y 2 > 1 arcsin x − arcsin y = { arcsin ( x 1 − y 2 − y 1 − x 2 ) , x y ≥ 0 nebo x 2 + y 2 ≤ 1 π − arcsin ( x 1 − y 2 − y 1 − x 2 ) , x > 0 , y < 0 , x 2 + y 2 > 1 − π − arcsin ( x 1 − y 2 − y 1 − x 2 ) , x < 0 , y > 0 , x 2 + y 2 > 1 {\displaystyle {\begin{array}{lcll}\arcsin x+\arccos x&=&{\frac {\pi }{2}}\\\arcsin x+\arcsin(-x)&=&0\\\arcsin x+\arcsin y&=&\left\{{\begin{array}{rl}\arcsin \left(x\,{\sqrt {1-y^{2}}}+y\,{\sqrt {1-x^{2}}}\right),&xy\leq 0\;\;{\mbox{nebo}}\;\;x^{2}+y^{2}\leq 1\\\pi -\arcsin \left(x\,{\sqrt {1-y^{2}}}+y\,{\sqrt {1-x^{2}}}\right),&x>0,\,y>0,\,x^{2}+y^{2}>1\\-\pi -\arcsin \left(x\,{\sqrt {1-y^{2}}}+y\,{\sqrt {1-x^{2}}}\right),&x<0,\,y<0,\,x^{2}+y^{2}>1\end{array}}\right.\\\arcsin x-\arcsin y&=&\left\{{\begin{array}{rl}\arcsin \left(x\,{\sqrt {1-y^{2}}}-y\,{\sqrt {1-x^{2}}}\right),&xy\geq 0\;\;{\mbox{nebo}}\;\;x^{2}+y^{2}\leq 1\\\pi -\arcsin \left(x\,{\sqrt {1-y^{2}}}-y\,{\sqrt {1-x^{2}}}\right),&x>0,\,y<0,\,x^{2}+y^{2}>1\\-\pi -\arcsin \left(x\,{\sqrt {1-y^{2}}}-y\,{\sqrt {1-x^{2}}}\right),&x<0,\,y>0,\,x^{2}+y^{2}>1\end{array}}\right.\\\end{array}}} arcsin ( sin x ) = x , − π 2 ≤ x ≤ π 2 sin ( arcsin x ) = x {\displaystyle {\begin{array}{lcll}\arcsin(\sin x)&=&x,&-{\frac {\pi }{2}}\leq x\leq {\frac {\pi }{2}}\\\sin(\arcsin x)&=&x\end{array}}}
arcsin x = ∫ 0 x d t 1 − t 2 , 0 < x < 1 {\displaystyle \arcsin x=\int _{0}^{x}{\frac {\mathrm {d} t}{\sqrt {1-t^{2}}}},\quad 0<x<1} arcsin x = x 1 − x 2 1 − 1 ⋅ 2 ⋅ x 2 3 − 1 ⋅ 2 ⋅ x 2 5 − 3 ⋅ 4 ⋅ x 2 7 − 3 ⋅ 4 ⋅ x 2 9 − 5 ⋅ 6 ⋅ x 2 11 − … , | x | < 1 {\displaystyle \arcsin x={\frac {x\,{\sqrt {1-x^{2}}}}{1-\displaystyle {\frac {1\cdot 2\cdot x^{2}}{3-\displaystyle {\frac {1\cdot 2\cdot x^{2}}{5-\displaystyle {\frac {3\cdot 4\cdot x^{2}}{7-\displaystyle {\frac {3\cdot 4\cdot x^{2}}{9-\displaystyle {\frac {5\cdot 6\cdot x^{2}}{11-\dots }}}}}}}}}}}},\quad |x|<1}
Mějme goniometrickou rovnici : [ 3]
2 sin x = 3 sin x = 3 2 x = arcsin 3 2 x = π 3 {\displaystyle {\begin{array}{rcl}2\sin x&=&{\sqrt {3}}\\\hline \sin x&=&{\frac {\sqrt {3}}{2}}\\x&=&\arcsin {\frac {\sqrt {3}}{2}}\\\hline x&=&{\frac {\pi }{3}}\end{array}}} S ohledem na periodicitu funkce sin x {\displaystyle \sin x} jsou řešením původní rovnice také hodnoty:
… , − 11 π 3 , − 5 π 3 , π 3 , 7 π 3 , 13 π 3 , … tj. x k = π 3 + 2 k π , k ∈ Z … , − 10 π 3 , − 4 π 3 , 2 π 3 , 8 π 3 , 14 π 3 , … tj. x k = 2 π 3 + 2 k π , k ∈ Z {\displaystyle {\begin{array}{rrrrrrrlr}\dots ,&{\color {OliveGreen}{\frac {-11\pi }{3}}},&{\color {OliveGreen}{\frac {-5\pi }{3}}},&\mathbf {\frac {\boldsymbol {\pi }}{3}} ,&{\color {OliveGreen}{\frac {7\pi }{3}}},&{\color {OliveGreen}{\frac {13\pi }{3}}},&\dots &\qquad {\mbox{tj.}}\quad \color {OliveGreen}{x_{k}=}&\color {OliveGreen}{{\frac {\pi }{3}}+2k\pi },\;k\in \mathbb {Z} \\\dots ,&{\color {BrickRed}{\frac {-10\pi }{3}}},&{\color {BrickRed}{\frac {-4\pi }{3}}},&{\color {BrickRed}{\frac {2\pi }{3}}},&{\color {BrickRed}{\frac {8\pi }{3}}},&{\color {BrickRed}{\frac {14\pi }{3}}},&\dots &\qquad {\mbox{tj.}}\quad \color {BrickRed}{x_{k}=}&\color {BrickRed}{{\frac {2\pi }{3}}+2k\pi },\;k\in \mathbb {Z} \end{array}}}
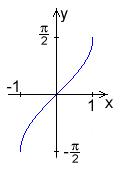
Graf Vznikne překlopením grafu funkce y = sin ( x ) {\displaystyle y=\sin(x)} kvadrantu . Bereme pouze interval kolem počátku , na kterém je funkce sin ( x ) {\displaystyle \sin(x)} prostá , tedy v tomto případě rostoucí. Interval ⟨ − π 2 , π 2 ⟩ {\displaystyle \textstyle \left\langle -{\frac {\pi }{2}},{\frac {\pi }{2}}\right\rangle } oborem hodnot funkce x = a r c s i n ( y ) {\displaystyle x=\mathrm {arcsin} (y)} Obdobně obor hodnot sinu se naopak stane definičním oborem arkus sinu. Graf funkce arkus sinus.
Odkazy
Reference ↑ KAREL REKTORYS A SPOLUPRACOVNÍCI. Přehled užité matematiky. 7. vyd. Praha: Prometheus, 2000. ISBN 8071961795 ↑ WolframAlpha: arcsin x ↑ WolframAlpha: 2sin(x)=√3
Obrázky, zvuky či videa k tématu arkus sinus Wikimedia Commons BARTSCH, Hans-Jochen. Matematické vzorce. 3., rev. vyd. Přeložil Zdeněk TICHÝ. Praha: Mladá fronta, 1996. ISBN 80-2040607-7 
 Obrázky, zvuky či videa k tématu arkus sinus na Wikimedia Commons
Obrázky, zvuky či videa k tématu arkus sinus na Wikimedia Commons 
