Atomový orbital

Atomový orbital (též pouze atomový orbit) je funkce popisující prostorové rozložení možného výskytu elektronu daného kvantového stavu v elektronovém obalu atomu.
Tento pojem nelze vysvětlit pomocí klasické planetární představy o struktuře atomu, kdy okolo jádra obíhají elektrony po jasně vymezených drahách podobně jako planety okolo Slunce. Elektron, jako každá elementární částice, vykazuje kvantové vlastnosti, které odpovídají jak částicím, tak vlnění (dualita částice a vlnění). V důsledku Heisenbergova principu neurčitosti nelze přesně stanovit polohu elektronu v atomu (v daném časovém okamžiku), proto musíme k popisu využít pravděpodobnost. Atomový orbital je popsán vlnovou funkcí elektronu v elektrickém poli nabitého jádra, která je řešením Schrödingerovy rovnice. Tato funkce je amplitudou pravděpodobnosti, že se v daném místě elektron vyskytuje (vlastní pravděpodobnost je pak dána druhou mocninou absolutní hodnoty vlnové funkce).
Pojem orbital se používá i pro názornější interpretaci vlnové funkce – pro geometrický útvar vymezující oblast, kde je vysoká pravděpodobnost výskytu daného elektronu (např. > 0,95), ohraničenou plochou stejné absolutní hodnoty amplitudy pravděpodobnosti. Z možných lineárních kombinací stavů se pro atomové orbitaly volí ty, které odpovídají sférickým harmonickým funkcím.[pozn. 1] Takové názorné zobrazení je u valenčních elektronů velmi užitečné pro posuzování chemických vlastností atomů a jejich vazeb s jinými atomy, aniž by bylo nutno provádět složité kvantově chemické výpočty.
Typy a tvary orbitalů
Typy orbitalů jsou dány hlavním a vedlejším kvantovým číslem daného elektronového stavu. Tvarovou formu daného typu určuje také magnetické kvantové číslo.
Typ orbitalu se pro l = 0 značí s, pro l = 1 p, pro l = 2 d, pro l = 3 f (značení ze spektroskopických anglických pojmů sharp, principal, diffuse, fundamental) a pro vyšší l (= 4, 5, …) se značí g, h, …(atd. dle abecedy). Nedílnou součástí typu orbitalu je hlavní kvantové číslo n příslušné energiové slupky atomového obalu (píše se před písmennou značkou typu).
Hlavní kvantové číslo má vliv především na velikost orbitalu. Čím je kvantové číslo n větší, tím větší je jeho energie a tím větší je také oblast pravděpodobného výskytu elektronu od jádra. Hlavní kvantové číslo nemá vliv na směrové rozložení pravděpodobnosti výskytu elektronu, projevuje se však v radiálním směru (tj. podle poloměru od středu atomového obalu, tedy od jádra): Pro vyšší n se v radiálním průběhu objevují body, ve kterých vlnová funkce přechází mezi zápornými a kladnými hodnotami, v okolí těchto bodů pravděpodobnost výskytu elektronu klesá a v bodě přechodu je nulová. Takové body nulové pravděpodobnosti výskytu leží na tzv. nodálních plochách, kterých je (n − 1).
Vliv hlavního kvantového čísla na velikost ukazují následující obrázky (orbitaly ns pro n = 1 až 7, v řezu, odlišná barva značí odlišné znaménko vlnové funkce):
Vliv hlavního kvantového čísla na tvar (přibývání nodálních ploch) na orbitalu složitějšího tvaru (pz pro n = 2 až 6; rozdílné měřítko, aby obrázky byly stejně veliké):
Tvar orbitalu je určen hlavně vedlejším a magnetickým kvantovým číslem (l a m):
Orbital s (l = 0) je kulově symetrický. Magnetické číslo může být jedině m = 0, a proto není degenerovaný (degenerovaný = více možností prostorové orientace při stejné energii).
Tvar orbitalu s (n = 1):
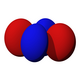
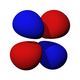
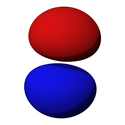
Orbital p (l = 1) má tvar dvou rotačně symetrických laloků, vzájemně středově symetricky vybíhajících od středu atomu do směru vybrané souřadné osy (v každém laloku má vlnová funkce jiné znaménko). Magnetické číslo může nabývat hodnot m = −1,0,1, orbital je tedy 3× degenerovaný. Prostorové formy se dle příslušných sférických harmonických funkcí označují px, py, pz v souladu se souřadnou osou, podle které je orbital souměrný; orbital pz odpovídá m = 0, zbylé dva jsou lineární kombinací stavů s m = −1,+1.
Tvary orbitalu p (px, py, pz; n = 2):
Orbital d (l = 2) má tvar složitější, členěný do více laloků, se vzájemně tvarově odlišnými formami. Orbital je 5× degenerovaný, magnetické číslo m = −2,−1,0,1,2. Prostorové formy se označují dxy, dxz, dyz, dx²-y², dz².
Tvary orbitalu d (dxy, dxz, dyz, dx²-y², dz²; n = 3):
Orbital f (l = 3) je 7× degenerovaný, magnetické číslo m = −3,−2,−1,0,1,2,3. Prostorové formy se označují fz³, fxz², fyz², fxyz, fz(x²-y²), fx(x²-3y²), fy(3x²-y²).
Tvary orbitalu f (f z³, fxz², fyz², fxyz, fz(x²-y²), fx(x²-3y²), fy(3x²-y²); n = 4):
Orbital g[pozn. 2] (l = 4) je 9× degenerovaný, magnetické číslo m = −4,−3,−2,−1,0,1,2,3,4; podobně pro vyšší l. Obecně platí, že orbitaly jsou (2l+1)-krát degenerované.
Zaplněnost orbitalů elektrony se označuje podle obecného vzorce
- n typy
- n odpovídá energii orbitalu (hlavní kvantové číslo elektronu)
- typ orbitalu se značí malým písmenem a popisuje tvar orbitalu, odpovídá momentu hybnosti (vedlejšímu kvantovému číslu l)
- y je obsazenost orbitalu elektrony.
Každý elektronový stav (daný vedle kvantových čísel n, l a m ještě spinovým kvantovým číslem s) může být v souladu s Pauliho vylučovacím principem obsazen pouze jedním elektronem; každý typ orbitalu proto může být obsazen počtem elektronů, daným dvojnásobkem (2 elektrony lišící se svým spinem) jeho degenerace.
Např. jediný plně obsazený orbital atomu helia v základním stavu se označuje 1s² – obsahuje 2 elektrony na nejnižší energiové úrovni (n = 1) a jejich moment hybnosti je l = 0.
Zaplnění orbitalů elektrony určuje pro jednotlivé atomy v základním stavu výstavbový princip, vyplývající z minimalizace potenciální energie elektronového obalu.
Poznámky
- ↑ Tato volba není nijak „umělá“, ale plyne z přirozeného požadavku aby z komplexních vlnových funkcí pro m ≠ 0 byly vytvořeny reálné kombinace a přitom byly směšovány pouze funkce se stejnou absolutní hodnotou m.
- ↑ Orbitaly g, h, … nejsou zaplněny v základních energetických stavech v žádném z dosud známých atomů. Příslušejí jistým vyšším energetickým stavům elektronů v obalu – i v atomu vodíku může být elektron ve vzbuzeném stavu odpovídajícím orbitalu g, dokud atom nepřejde do stabilního základního stavu. První prvek v základním stavu s částečně zaplněným orbitalem g by měl být prvek s protonovým číslem 121.
Související články
Externí odkazy
 Obrázky, zvuky či videa k tématu atomový orbital na Wikimedia Commons
Obrázky, zvuky či videa k tématu atomový orbital na Wikimedia Commons - (anglicky) Galerie atomových orbitalů Orbitron (University of Sheffield))
Média použitá na této stránce
Created in Orbital viewer [1]. Part of the electron orbital series. Quantum numbers: n=4, l=3, mz=±2 (superposition).
Created in Orbital viewer [1]. Part of the electron orbital series. Quantum numbers: n=3, l=2, mz=±2 (superposition).
Created in Orbital viewer [1]. Part of the electron orbital series. Quantum numbers: n=4, l=3, mz=±3 (superposition).
Created in Orbital viewer [1]. Part of the electron orbital series. Quantum numbers: n=4, l=3, mz=±3 (superposition).
Autor: Geek3, Licence: CC BY-SA 3.0
Calculated 2s0orbital of an electron's eigenstate in the Coulomb-field of a hydrogen nucleus. An eigenstate is a state which keeps it's shape except for a complex phase when the Hamilton operator is applied, thus being invariant in time while obeying the Schrödinger equation.
The wavefunction is:
The state is an eigenstate of H, L² and Lz, which constitute a complete set of commuting observables.
The quantum numbers mean that the following quantities have a sharp certain value:
- n = 2: Energy:
- l = 0: Angular momentum:
- m = 0: Angular momentum in z-direction:
Since l=0, this is called a s-orbital.
The depicted rigid body is where the probability density exceeds a certain value. The color shows the complex phase of the wavefunction, where blue means real positive, red means imaginary positive, yellow means real negative and green means imaginary negative. The image is raytraced using modified Phong lighting.
Electron orbitals