Axonometrie

(c) I, Chabacano, CC BY-SA 3.0

Axonometrie nebo axonometrická projekce je jednoduchý způsob promítání prostorových těles a trojrozměrných struktur (3D) do roviny.

V rovině se nejprve zvolí tři osy x, y a z, jež spolu svírají stejné nebo nestejné úhly. Rozměry těles se pak nanášejí v určitém měřítku rovnoběžně s těmito osami: odtud také název, doslova „odměřovat podél os“. Hlavní výhoda axonometrie proti složitějším metodám promítání je v tom, že se průmět snadno konstruuje a že se z něho dají rozměry odečíst. Nevýhoda může být v tom, že v axonometrické projekci se rovnoběžky nesbíhají a tak je perspektivní dojem nedokonalý. To může působit jako vizuální paradox, známý například z kreseb malíře M. C. Eschera.

Osy axonometrického promítání lze zvolit libovolně, obvykle se však osa z („výška“) volí jako svislá. Nejčastěji užívané varianty axonometrie jsou:

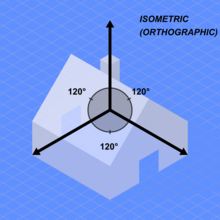
• Izometrie, při níž tři osy navzájem svírají úhel 120° a všechny délky se nanášejí ve stejném měřítku (1:1:1).
• Dimetrie, kde úhel mezi osami x a y je větší než 120° a zbývající dva úhly jsou menší; délky se nanášejí v měřítku 1:0,5:1. Jeden z rozměrů se tedy zkracuje na polovinu.
• Trimetrie, kde jsou všechny tři úhly různé a délky se také nanášejí ve třech měřítkách, například 0,9:0,5:1.
• Vojenská perspektiva, kde osy x a y svírají úhel 90°, kdežto výška se nanáší na šikmou osu. Všechny vzdálenosti se nanášejí isometricky, v tomtéž měřítku (1:1:1).

• Ottův slovník naučný, heslo Axonometrie. Sv. 2, str. 1117

• Deskriptivní geometrie
• Izometrie
• Perspektivní promítání
• Pravoúhlé promítání
• Kosoúhlé promítání

• (anglicky) P. Maynard: Drawing distinctions, Google books
• (německy) Axonometrie, konstrukce a vzorce