Besselovy funkce jsou řešení Besselovy rovnice
z 2 d 2 w ( z ) d z 2 + z d w ( z ) d z + ( z 2 − ν 2 ) w ( z ) = 0 {\displaystyle z^{2}{\frac {\mathrm {d} ^{2}w(z)}{\mathrm {d} z^{2}}}+z{\frac {\mathrm {d} w(z)}{\mathrm {d} z}}+(z^{2}-\nu ^{2})w(z)=0} pro libovolné reálné číslo ν {\displaystyle \nu } řád Besselovy funkce . Funkce jsou pojmenovány na počest německého matematika a fyzika Friedricha Wilhelma Bessela , který je poprvé popsal.
Cylindrické funkce Cylindrickou funkcí se nazývá libovolné řešení Besselovy rovnice
Besselova funkce Není-li ν {\displaystyle \nu } celé číslo , pak lze obecné řešení Besselovy rovnice zapsat jako
w ( z ) = c 1 J ν ( z ) + c 2 J − ν ( z ) {\displaystyle w(z)=c_{1}J_{\nu }(z)+c_{2}J_{-\nu }(z)} kde J ν ( z ) {\displaystyle J_{\nu }(z)} J − ν ( z ) {\displaystyle J_{-\nu }(z)} lineárně nezávislé Besselovy funkce a c 1 , c 2 {\displaystyle c_{1},c_{2}} konstanty .
Besselovy funkce bývají také nazývány Besselovými funkcemi prvního druhu .
Besselova funkce řádu ν {\displaystyle \nu }
J ν ( z ) = ( z 2 ) ν ∑ k = 0 ∞ ( − 1 ) k k ! Γ ( ν + k + 1 ) ( z 2 ) 2 k {\displaystyle J_{\nu }(z)={\left({\frac {z}{2}}\right)}^{\nu }\sum _{k=0}^{\infty }{\frac {{(-1)}^{k}}{{k!}\Gamma (\nu +k+1)}}{\left({\frac {z}{2}}\right)}^{2k}} kde Γ ( x ) {\displaystyle \Gamma (x)} gama funkce .
Je-li ν = n {\displaystyle \nu =n}
J − n ( z ) = ( − 1 ) n J n ( z ) {\displaystyle J_{-n}(z)={(-1)}^{n}J_{n}(z)} výše uvedená řešení tedy nejsou v tomto případě nezávislá.
Pro n = 0 , 1 , 2 , . . . {\displaystyle n=0,1,2,...}
J n ( z ) = 1 π ∫ 0 π cos ( z sin θ − n θ ) d θ {\displaystyle J_{n}(z)={\frac {1}{\pi }}\int _{0}^{\pi }\cos(z\sin \theta -n\theta )\mathrm {d} \theta } Platí následující rekurentní vztahy
2 ν J ν ( z ) = z J ν − 1 ( z ) + z J ν + 1 ( z ) {\displaystyle 2\nu J_{\nu }(z)=zJ_{\nu -1}(z)+zJ_{\nu +1}(z)} 2 J ν ′ ( z ) = J ν − 1 ( z ) − J ν + 1 ( z ) {\displaystyle 2J_{\nu }^{\prime }(z)=J_{\nu -1}(z)-J_{\nu +1}(z)} z J ν ′ ( z ) = ν J ν ( z ) − z J ν + 1 ( z ) {\displaystyle zJ_{\nu }^{\prime }(z)=\nu J_{\nu }(z)-zJ_{\nu +1}(z)} z J ν ′ ( z ) = − ν J ν ( z ) + z J ν − 1 ( z ) {\displaystyle zJ_{\nu }^{\prime }(z)=-\nu J_{\nu }(z)+zJ_{\nu -1}(z)} Neumannova funkce Je-li ν = n {\displaystyle \nu =n} celé číslo , pak J n ( z ) {\displaystyle J_{n}(z)} J − n ( z ) {\displaystyle J_{-n}(z)} lineárně nezávislé . V takovém případě má obecný integrál tvar
w ( z ) = c 1 J n ( z ) + c 2 N n ( z ) {\displaystyle w(z)=c_{1}J_{n}(z)+c_{2}N_{n}(z)} kde N n ( z ) {\displaystyle N_{n}(z)} Neumannova funkce (někdy též Weberova funkce ), které jsou také řešením Besselovy rovnice.
Pro Neumannovy funkce se používá označení Besselovy funkce druhého druhu .
Neumannovy funkce jsou pro celočíselná ν = n {\displaystyle \nu =n}
N n ( z ) = lim ν → n J ν ( z ) cos ν π − J − ν ( z ) sin ν π {\displaystyle N_{n}(z)=\lim _{\nu \to n}{\frac {J_{\nu }(z)\cos \nu \pi -J_{-\nu }(z)}{\sin \nu \pi }}} Pro ν {\displaystyle \nu }
N ν ( z ) = J ν ( z ) cos ν π − J − ν ( z ) sin ν π {\displaystyle N_{\nu }(z)={\frac {J_{\nu }(z)\cos \nu \pi -J_{-\nu }(z)}{\sin \nu \pi }}} Je-li ν = n {\displaystyle \nu =n}
N − n ( z ) = ( − 1 ) n N n ( z ) {\displaystyle N_{-n}(z)={(-1)}^{n}N_{n}(z)} Mezi Besselovými a Neumannovými funkcemi platí vztah
J ν ( z ) N ν + 1 ( z ) − J ν + 1 ( z ) N ν ( z ) = − 2 π z {\displaystyle J_{\nu }(z)N_{\nu +1}(z)-J_{\nu +1}(z)N_{\nu }(z)=-{\frac {2}{\pi z}}} Platí následující rekurentní vztahy
2 ν N ν ( z ) = z N ν − 1 ( z ) + z N ν + 1 ( z ) {\displaystyle 2\nu N_{\nu }(z)=zN_{\nu -1}(z)+zN_{\nu +1}(z)} 2 N ν ′ ( z ) = N ν − 1 ( z ) − N ν + 1 ( z ) {\displaystyle 2N_{\nu }^{\prime }(z)=N_{\nu -1}(z)-N_{\nu +1}(z)} z N ν ′ ( z ) = ν N ν ( z ) − z N ν + 1 ( z ) {\displaystyle zN_{\nu }^{\prime }(z)=\nu N_{\nu }(z)-zN_{\nu +1}(z)} z N ν ′ ( z ) = − ν N ν ( z ) + z N ν − 1 ( z ) {\displaystyle zN_{\nu }^{\prime }(z)=-\nu N_{\nu }(z)+zN_{\nu -1}(z)} Hankelova funkce Důležitými cylindrickými funkcemi jsou tzv. Hankelovy funkce H ν ( 1 ) ( z ) {\displaystyle H_{\nu }^{(1)}(z)} H ν ( 2 ) ( z ) {\displaystyle H_{\nu }^{(2)}(z)}
H ν ( 1 ) ( z ) = J ν ( z ) + i N ν ( z ) {\displaystyle H_{\nu }^{(1)}(z)=J_{\nu }(z)+\mathrm {i} N_{\nu }(z)} H ν ( 2 ) ( z ) = J ν ( z ) − i N ν ( z ) {\displaystyle H_{\nu }^{(2)}(z)=J_{\nu }(z)-\mathrm {i} N_{\nu }(z)} Hankelova funkce bývá také označována jako Besselova funkce třetího druhu .
Sférické cylindrické funkce Sférickou cylindrickou funkcí nazveme každé řešení rovnice
z 2 d 2 w ( z ) d z 2 + 2 z d w ( z ) d z + [ z 2 − l ( l + 1 ) ] w ( z ) = 0 {\displaystyle z^{2}{\frac {\mathrm {d} ^{2}w(z)}{\mathrm {d} z^{2}}}+2z{\frac {\mathrm {d} w(z)}{\mathrm {d} z}}+\left[z^{2}-l(l+1)\right]w(z)=0} pro celá nezáporná l {\displaystyle l}
Za dvě nezávislá řešení lze zvolit sférickou Besselovu funkci
j l ( z ) = π 2 z J l + 1 2 ( z ) {\displaystyle j_{l}(z)={\sqrt {\frac {\pi }{2z}}}J_{l+{\frac {1}{2}}}(z)} a sférickou Neumannovu funkci
n l ( z ) = π 2 z N l + 1 2 ( z ) = ( − 1 ) l + 1 π 2 z J − l − 1 2 ( z ) {\displaystyle n_{l}(z)={\sqrt {\frac {\pi }{2z}}}N_{l+{\frac {1}{2}}}(z)={(-1)}^{l+1}{\sqrt {\frac {\pi }{2z}}}J_{-l-{\frac {1}{2}}}(z)} kde J n {\displaystyle J_{n}} N n {\displaystyle N_{n}}
Mezi sférickými Besselovými a sférickými Neumannovými funkcemi platí vztah
j l ( z ) n l + 1 ( z ) − j l + 1 ( z ) n l ( z ) = − z − 2 {\displaystyle j_{l}(z)n_{l+1}(z)-j_{l+1}(z)n_{l}(z)=-z^{-2}} Jinou dvojicí nezávislých řešení jsou sférické Hankelovy funkce
h l ( 1 ) ( z ) = j l ( z ) + i n l ( z ) {\displaystyle h_{l}^{(1)}(z)=j_{l}(z)+\mathrm {i} n_{l}(z)} h l ( 2 ) ( z ) = j l ( z ) − i n l ( z ) {\displaystyle h_{l}^{(2)}(z)=j_{l}(z)-\mathrm {i} n_{l}(z)} Sférické cylindrické funkce lze vyjádřit následujícími vztahy
j l ( z ) = ( − z ) l ( d z d z ) l sin z z {\displaystyle j_{l}(z)={(-z)}^{l}{\left({\frac {\mathrm {d} }{z\mathrm {d} z}}\right)}^{l}{\frac {\sin z}{z}}} n l ( z ) = − ( − z ) l ( d z d z ) l cos z z {\displaystyle n_{l}(z)=-{(-z)}^{l}{\left({\frac {\mathrm {d} }{z\mathrm {d} z}}\right)}^{l}{\frac {\cos z}{z}}} h l ( 1 ) ( z ) = − i ( − z ) l ( d z d z ) l e i z z {\displaystyle h_{l}^{(1)}(z)=-\mathrm {i} {(-z)}^{l}{\left({\frac {\mathrm {d} }{z\mathrm {d} z}}\right)}^{l}{\frac {\mathrm {e} ^{\mathrm {i} z}}{z}}} Lze ukázat, že platí
j l ( − z ) = ( − 1 ) l j l ( z ) {\displaystyle j_{l}(-z)={(-1)}^{l}j_{l}(z)} n l ( − z ) = ( − 1 ) l + 1 n l ( z ) {\displaystyle n_{l}(-z)={(-1)}^{l+1}n_{l}(z)} h l ( 1 ) ( − z ) = ( − 1 ) l h l ( 2 ) ( z ) {\displaystyle h_{l}^{(1)}(-z)={(-1)}^{l}h_{l}^{(2)}(z)} h l ( 2 ) ( − z ) = ( − 1 ) l h l ( 1 ) ( z ) {\displaystyle h_{l}^{(2)}(-z)={(-1)}^{l}h_{l}^{(1)}(z)} Modifikovaná Besselova funkce Modifikované Besselovy funkce jsou řešením modifikované Besselovy rovnice
z 2 d 2 w ( z ) d z 2 + z d w ( z ) d z − ( z 2 + ν 2 ) w ( z ) = 0 {\displaystyle z^{2}{\frac {\mathrm {d} ^{2}w(z)}{\mathrm {d} z^{2}}}+z{\frac {\mathrm {d} w(z)}{\mathrm {d} z}}-(z^{2}+\nu ^{2})w(z)=0} Modifikovaná Besselova funkce prvního druhu Není-li ν {\displaystyle \nu }
w ( z ) = c 1 I ν ( z ) + c 2 I − ν ( z ) {\displaystyle w(z)=c_{1}I_{\nu }(z)+c_{2}I_{-\nu }(z)} kde I ν ( z ) {\displaystyle I_{\nu }(z)} modifikovaná Besselova funkce prvního druhu , která je definována vztahem
I ν ( z ) = ( z 2 ) ν ∑ k = 0 ∞ 1 K ! Γ ( ν + k + 1 ) ( z 2 ) 2 k {\displaystyle I_{\nu }(z)={\left({\frac {z}{2}}\right)}^{\nu }\sum _{k=0}^{\infty }{\frac {1}{{K!}\Gamma (\nu +k+1)}}{\left({\frac {z}{2}}\right)}^{2k}} Modifikovanou Besselovu funkci lze vyjádřit pomocí Besselovy funkce jako
I ν ( z ) = i − ν J ν ( i z ) {\displaystyle I_{\nu }(z)=\mathrm {i} ^{-\nu }J_{\nu }(\mathrm {i} z)} Modifikovaná Besselova funkce druhého druhu Pro celá ν = n {\displaystyle \nu =n}
I − n ( z ) = I n ( z ) {\displaystyle I_{-n}(z)=I_{n}(z)} Pro celá n {\displaystyle n} I n ( z ) {\displaystyle I_{n}(z)} I − n ( z ) {\displaystyle I_{-n}(z)}
w ( z ) = c 1 I n ( z ) + c 2 K n ( z ) {\displaystyle w(z)=c_{1}I_{n}(z)+c_{2}K_{n}(z)} kde K n ( z ) {\displaystyle K_{n}(z)} modifikovaná Besselova funkce druhého druhu (označovaná též jako MacDonaldova funkce ).
Pro necelé ν {\displaystyle \nu }
K ν ( z ) = π 2 I − ν ( z ) − I ν ( z ) sin ν π {\displaystyle K_{\nu }(z)={\frac {\pi }{2}}{\frac {I_{-\nu }(z)-I_{\nu }(z)}{\sin \nu \pi }}} Pro celá ν = n {\displaystyle \nu =n}
K n ( z ) = lim ν → n π 2 I − ν ( z ) − I ν ( z ) sin ν π {\displaystyle K_{n}(z)=\lim _{\nu \to n}{\frac {\pi }{2}}{\frac {I_{-\nu }(z)-I_{\nu }(z)}{\sin \nu \pi }}} Fresnelův ohyb světla na hraně Důležitým příkladem použití Besselových funkcí je Fresnelův ohyb světla na hraně .
Ohyb světla na přímé hraně.monochromatickým světlem dochází při ohybu na hraně ke vzniku ohybových proužků, které jsou rovnoběžné s přímou hranou.intenzity světla . Související články Externí odkazy Literatura Rektorys, K. a spol.: Přehled užité matematiky I. . Prometheus, Praha, 2003 , 7. vydání. ISBN 80-7196-179-5 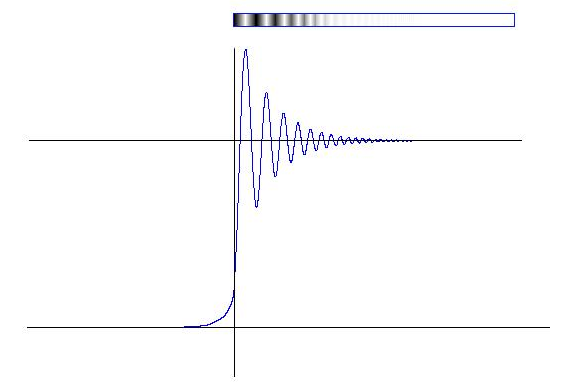
 Obrázky, zvuky či videa k tématu Besselova funkce na Wikimedia Commons
Obrázky, zvuky či videa k tématu Besselova funkce na Wikimedia Commons 