Cassegrainův dalekohled

Cassegrainova soustava (Cassegrainův systém, případně jen Cassegrain) je konstrukce často používaná pro optické dalekohledy a rádiové antény, která kombinuje primární vyduté zrcadlo a sekundární vypuklé zrcadlo. Světelné paprsky odražené primárním zrcadlem se odrážejí sekundárním zrcadlem zpět do prostoru za primární zrcadlo (obvykle do otvoru v primárním zrcadle). Díky tomu je okulár na vhodném místě a vypuklé sekundární zrcadlo zároveň prodlužuje ohniskovou délku celého systému, takže lze dosáhnout většího zvětšení v mechanicky krátkém systému.^[1]

Podobnou konstrukcí je Gregoryho dalekohled, u něhož je sekundární zrcadlo vyduté a umístěné až za ohniskem primárního zrcadla.

V symetrické Cassegrainově konstrukci jsou obě zrcadla vystředěna kolem optické osy a primární zrcadlo má uprostřed otvor, kterým prochází světlo na okulár, do fotoaparátu nebo obrazového snímače. Jinou možností, častou u rádiových dalekohledů, je závěrečné ohnisko před primárním zrcadlem. V asymetrické Cassegrainově konstrukci jsou použity části optických ploch, které nejsou symetrické vůči optické ose, aby se zabránilo stínění primárního zrcadla nebo aby nebyl potřebný otvor v primárním zrcadle (nebo obojí).

Klasická Cassegrainova konfigurace používá parabolický reflektor jako primární zrcadlo, a sekundární zrcadlo je hyperbolické.^[2] Moderní varianty mohou mít hyperbolické primární zrcadlo pro zvětšení výkonnosti (například Ritcheyova–Chrétienova konstrukce); a jedno ze zrcadel (příp. obě) může být sférické nebo eliptické pro usnadnění výroby.

Cassegrainův reflektor je pojmenovaný podle popisu zrcadlového dalekohledu publikovaném 25. dubna 1672 v Journal des sçavans, který je připisován Laurentovi Cassegrainovi.^[3] Podobné konstrukce používající konvexní sekundární zrcadlo byly nalezeny v knize Bonaventury Cavalieriho z roku 1632 popisujícím zapalovací zrcadla^[4][5] a spisku Marina Mersenneho z roku 1636 popisujícím konstrukce dalekohledů.^[6] Soudě podle nalezeného vypouklého zrcadla James Gregory při svých pokusech v roce 1662 zkoušel i konfiguraci Cassegrain, ale nakonec použil systém s vydutým sekundárním zrcadlem.^[7]

Cassegrainova konstrukce se také používá v katadioptrických systémech.

Cassegrainova konstrukce

“Klasické“ Cassegrainovy dalekohledy

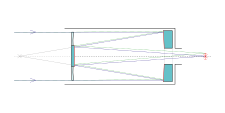
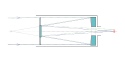
„Klasický“ Cassegrain má parabolické primární zrcadlo a hyperbolické sekundární zrcadlo, které odráží světlo zpět dolů otvorem v primárním zrcadle. Díky tomuto odrazu je dalekohled kratší než by odpovídalo ohniskové délce zrcadla. U menších dalekohledů a objektivů fotoaparátů je sekundární zrcadlo často namontováno na ploché, průhledné skleněné desce, která uzavírá tubus dalekohledu. Tento způsob uchycení odstraňuje difrakční efekty „hvězdicovitého tvaru“ způsobené přímým držákem. Uzavřený tubus zůstává čistý, a primární zrcadlo je chráněné, ovšem za cenu určitých světelných ztrát.

Konstrukce využívá speciálních vlastností parabolických a hyperbolických zrcadel. Konkávní parabolický reflektor odráží všechny přicházející světelné paprsky rovnoběžně se svou osou symetrie do jediného bodu, ohniska. Konvexní hyperbolický reflektor má dvě ohniska a odráží všechny světelné paprsky orientované do jednoho svého ohniska směrem k druhému. Zrcadla v tomto typu dalekohledu jsou navržena a umístěna tak, aby měla společné jedno ohnisko, a aby druhé ohnisko hyperbolického zrcadla bylo v bodě, v němž má být pozorován obraz, obvykle těsně za okulárem. Parabolické zrcadlo odráží rovnoběžné světelné paprsky vstupující do dalekohled do jeho ohniska, které je také ohniskem hyperbolického zrcadla. Hyperbolické zrcadlo pak odráží tyto světelné paprsky do svého druhého ohniska, kde je obraz pozorován.

Ve většině Cassegrainových systémů sekundární zrcadlo zakrývá středovou část apertury. Tato prstencovitá vstupní apertura, oproti konstrukcím s plnou aperturou např. v čočkovém dalekohledu nebo vyoseném Cassegrainově systému výrazně omezuje část modulační přenosové funkce (MTF) v rozsahu nízkých prostorových frekvencí.^[8] Tento MTF výřez způsobuje snížení kontrastu obrazu při zobrazování širokých objektů. Navíc uchycení sekundárního zrcadla (spider) může v obrazu způsobovat difrakční hroty.

Poloměry zakřivení primárního a sekundárního zrcadla v klasické konfiguraci jsou

${\displaystyle R_{1}=-{\frac {2DF}{F-B}}=-{\frac {2F}{M}}}$

a

${\displaystyle R_{2}=-{\frac {2DB}{F-B-D}}=-{\frac {2B}{M-1}}}$

kde

• ${\displaystyle F}$ je efektivní ohnisková vzdálenost systému,
• ${\displaystyle B}$ je zpětná ohnisková délka (vzdálenost od sekundárního zrcadla do ohniska),
• ${\displaystyle D}$ je vzdálenost mezi oběma zrcadly a
• ${\displaystyle M=(F-B)/D}$ je sekundární zvětšení

Pokud místo ${\displaystyle B}$ a ${\displaystyle D}$ je známa ohnisková délka primárního zrcadla ${\displaystyle f_{1}}$, a vzdálenost ohniska za primárním zrcadlem ${\displaystyle b}$, pak ${\displaystyle D=f_{1}(F-b)/(F+f_{1})}$ a ${\displaystyle B=D+b}$.

Kuželová konstanta primárního zrcadla je stejná jako u paraboly, ${\displaystyle K_{1}=-1}$. Díky tomu nedochází k žádné sférické aberaci způsobené primárním zrcadlem. Sekundární zrcadlo však má hyperbolický tvar a jedno ohnisko se shoduje s ohniskem primárního zrcadla a druhé tvoří výslednou ohniskovou vzdálenost ${\displaystyle B}$. Klasický Cassegrain má tedy ideální ohnisko pro hlavní paprsek (středový bodový diagram je jeden bod). Zde máme

${\displaystyle K_{2}=-1-\alpha -{\sqrt {\alpha (\alpha +2)}}}$,

kde

${\displaystyle \alpha ={\frac {1}{2}}\left[{\frac {4DBM}{(F+BM-DM)(F-B-D)}}\right]^{2}}$.

Protože kuželové konstanty nesmí záviset na zvětšení, vzorce pro ${\displaystyle \alpha }$ i ${\displaystyle K_{2}}$ lze značně zjednodušit a vyjádřit pouze jako funkce sekundárního zvětšení. Následně dostáváme

${\displaystyle \alpha ={\frac {8M^{2}}{(M^{2}-1)^{2}}}}$

a

${\displaystyle K_{2}=-1-{\frac {4M}{(M-1)^{2}}}=-\left({\frac {M+1}{M-1}}\right)^{2}}$.

Ritcheyův-Chrétienův dalekohled

Ritchey-Chrétien je specializovaný Cassegrainův reflektor který má dvě hyperbolická zrcadla (místo parabolického primárního). Netrpí komou ani sférickou aberací v ploché ohniskové rovině, což je vhodné pro široké pole a fotografická pozorování. Autory konstrukce ze začátku 10. let 20. století jsou George Willis Ritchey a Henri Chrétien. Tato konstrukce je často používaná u velkých profesionálních výzkum dalekohledů, včetně Hubbleova vesmírného dalekohledu, Keckových dalekohledů, a Very Large Telescope (VLT); také se používá ve vysoce kvalitních amatérských dalekohledech.

Dallův-Kirkhamův dalekohled

Dallovu-Kirkhamovu konstrukci Cassegrainova dalekohledu vytvořil Horace Dall v roce 1928; své jméno získala díky článku publikovaném v časopise Scientific American v roce 1930 a následující diskuzi mezi amatérským astronomem Allanem Kirkhamem a Albertem G. Ingallsem, který byl v té době redaktorem pro astronomii. Používá konkávní eliptické primární zrcadlo a konvexní sférické sekundární zrcadlo. Tento systém lze snáze vyladit než klasický Cassegrainův nebo Ritcheyův-Chretienův systém, ale mimoosová koma je výrazně horší, takže obraz se mimo osu rychle zhoršuje. Tento efekt je méně významný pro delší clonová čísla, proto se systém zřídka používá pro větší než f/15.

Mimoosové konfigurace

Neobvyklou variantou Cassegrainovy konstrukce je Schiefspieglerův dalekohled („šikmý reflektor“; také známý jako „Kutterův dalekohled“ po svém objeviteli, Antonu Kutterovi^[9]) který používá šikmé zrcadlo, aby sekundární zrcadlo nezastiňovalo primární. Odstranění difrakce však způsobuje několik jiných aberací, které musí být korigovány.

Několik různých mimoosových konfigurací se používá pro rádiové antény.^[10]

Další mimoosovou nestíněnou konstrukcí a variantou Cassegrainovy konstrukce je reflektor Yolo, který vynalezl Arthur Leonard. Jeho konstrukce používá sférické nebo parabolické primární zrcadlo a mechanicky tvarované sférické sekundární zrcadlo ke korekci mimoosového astigmatismu. Yolo může při správném nastavení poskytovat nekompromisní nestíněný pohled na planetární objekty a cíle, které nejsou v příliš širokém poli, bez problémů s kontrastem nebo kvalitou obrazu způsobených kulovou (či sférickou či otvorovou) vadou. Neexistence překážek také odstraňuje difrakce typické pro astrofotografie pořízené Cassegrainovy a Newtonovy dalekohledy.

Katadioptrické Cassegrainovy dalekohledy

Katadioptrické Cassegrainovy dalekohledy používají dvě zrcadla, přičemž primární zrcadlo je často sférické pro snížení ceny, kombinované s čočkovým korekčním prvkem nebo prvky pro korekci zbývajících aberací.

Schmidtův-Cassegrainův dalekohled

Chod paprsků v Schmidtově-Cassegrainově dalekohledu

Chod paprsků v Maksutovově-Cassegrainově dalekohledu

Chod paprsků v Klevtsovově-Cassegrainově dalekohledu

Schmidtův-Cassegrainův dalekohled byl vyvinut z širokoúhlé Schmidtovy komory, která však má v Cassegrain konfiguraci mnohem užší zorné pole. Prvním optickým prvkem je Schmidtova korekční destička. Deska je figurována odčerpáním vzduchu na jedné straně, a vybroušena tak, aby se přesně opravila sférická aberace způsobená sférickým primárním zrcadlem. Schmidtovy-Cassegrainovy dalekohledy jsou oblíbené u amatérských astronomů. Ranou Schmidtovu-Cassegrainovu komoru si dal v roce 1946 patentovat umělec, architekt a fyzik Roger Hayward,^[11] s držákem filmu umístěným mimo dalekohled.

Maksutovův-Cassegrainův dalekohled

Maksutovův-Cassegrainův dalekohled je varianta Maksutovova dalekohledu pojmenovaná po sovětském optikovi a astronomovi Dmitriji Dmitrijeviči Maksutovovi. Světlo nejprve prochází korekční čočkou, která je částí duté sféry. Primární i sekundární zrcadlo je sférické, přičemž sekundární je tvořeno odraznou úpravou zadní části korekční čočky.

Argunovův-Cassegrainův dalekohled

V Argunovově-Cassegrainově dalekohledu je také veškerá optika sférická, a klasické Cassegrainovo sekundární zrcadlo je nahrazeno subaperturním korektorem sestávajícím z tří oddělených čoček. Nejvzdálenějším prvkem od primárního zrcadla je Manginovo zrcadlo, které funguje jako sekundární zrcadlo.

Klevtsovův-Cassegrainův dalekohled

Klevtsovův-Cassegrainův systém používá jako Argunovův-Cassegrainův systém subaperturní korektor sestávající z malé meniskové čočky a sekundárního Manginova zrcadla.^[12]

Cassegrainovy rádiové antény

Cassegrainova konstrukce se také používá pro antény pozemních stanic pro satelitní telekomunikaci a radioteleskopy s velikostmi 2,4-70 metrů. Centrálně umístěný sekundární reflektor slouží k soustředění vysokofrekvenčního signálu podobným způsobem jako u optických dalekohledů.

Příkladem Cassegrainovy rádiové antény je sedmdesátimetrová anténa v Goldstonově radioastronomické observatoři, kterou spravuje Jet Propulsion Laboratory. U této antény je výsledné ohnisko je před primárním zrcadlem, ve vrchní části nosiče vystupujícího ze zrcadla.

Odkazy

Reference

V tomto článku byl použit překlad textu z článku Cassegrain reflector na anglické Wikipedii.

Související články

• Katadioptrický systém
• Zrcadlový dalekohled
• Refraktor
• Meade Instruments

Externí odkazy

• Obrázky, zvuky či videa k tématu Cassegrainův dalekohled na Wikimedia Commons

Literatura

• CAVALIERI, Bonaventura, 1632. Lo specchio ustorio, overo, Trattato delle settioni coniche [online]. 1632. Dostupné online. 
• WATSON, Fred, 2006. Stargazer, the Life and Times of the Telescope. [s.l.]: Da Capo Press. 368 s. p. 134 Dostupné online. ISBN 0306814838.