Cliffordův torus

Cliffordův torus (pojmenovaný po Williamu Kingdonu Cliffordovi) je v geometrické topologii nejjednodušší a nejsymetričtější ploché vložení kartézského součinu dvou jednotkových kružnic S 1
a  a S 1
b  (ve stejném smyslu, v němž je „plochý“ povrch válce). Cliffordův torus nepatří do prostoru R³, ale do R⁴. Pro pochopení, proč je nestačí R³, je třeba si všimnout, že pokud S 1
a  i S 1
b  existují ve vlastních nezávislých vložených prostorech R 2
a  a R 2
b , výsledný součinový prostor bude R⁴, nikoli R³. Historicky oblíbená představa, že kartézský součin dvou kružnic je R³-torus, naopak vyžaduje vysoce asymetrickou aplikaci operátoru rotace na druhou kružnici, aby tato kružnice měla pouze jednu nezávislou osu z, když pro první kružnici byly použity osy x a y.

Jinak řečeno, vložení toru do R³ je asymetrická projekce, která snižuje počet rozměrů maximálně symetrického Cliffordova toru vloženého do R⁴, obdobná projekci hran krychle na list papíru. Taková projekce vytváří obraz s menším počtem rozměrů, který sice přesně zachycuje propojení hran krychle, ale vyžaduje výběr a odstranění jedné ze tří plně symetrických a zaměnitelných os krychle.

Pokud obě kružnice S 1
a  a S 1
b  mají poloměr ${\displaystyle \textstyle {\sqrt {1/2}}}$, jejich součin vytvářející Cliffordův torus se přesně vejde do jednotkové 3-sféry S³, která je 3rozměrnou podvarietou R⁴. Je-li to matematicky pohodlné, můžeme předpokládat, že Cliffordův torus je umístěný v prostoru komplexních souřadnic C², protože C² je topologicky ekvivalentní s R⁴.

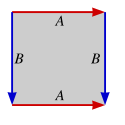
Cliffordův torus je příkladem čtvercového toru, protože je izometrií čtverce se ztotožněnými opačnými stranami. Je také znám jako Eukleidovský 2-torus (“2“ je jeho topologický rozměr); obrazec zvolený tak, aby zachovával Eukleidovskou geometrii^[ujasnit] jako, pokud ono byly plochý, zatímco povrch běžné „Americké koblihy“-tvarován torus je kladně zakřivený na vnější hranici a záporně zakřivený na vnitřní. Přestože má jinou geometrii než standardní vložení toru do trojrozměrného eukleidovského prostoru, může být čtvercový torus také vložen do trojrozměrného prostoru podle Nashovy věty o vložení; jedno možné vložení mění standardní torus na fraktální množinu vlnek běžících ve dvou kolmých směrech po povrchu.^[1]

Jednotková kružnice S¹ v R² může být parametrizován úhlem souřadnic:

${\displaystyle S^{1}=\{(\cos \theta ,\sin \theta )\mid 0\leq \theta <2\pi \}.}$

V jiný kopii R², nabývá jiné kopie jednotkové kružnice

${\displaystyle S^{1}=\{(\cos \varphi ,\sin \varphi )\mid 0\leq \varphi <2\pi \}.}$

Pak Cliffordův torus je

${\displaystyle {\tfrac {1}{\sqrt {2}}}S^{1}\times {\tfrac {1}{\sqrt {2}}}S^{1}=\{{\tfrac {1}{\sqrt {2}}}(\cos \theta ,\sin \theta ,\cos \varphi ,\sin \varphi )\mid 0\leq \theta <2\pi ,0\leq \varphi <2\pi \}.}$

Protože každá kopie S¹ je vložení podvarieta R², Cliffordův torus je vložený torus v R² × R² = R⁴.

Pokud R⁴ popisuje vztah souřadnic (x₁, y₁, x₂, y₂), pak Cliffordův torus popisuje vztah

${\displaystyle x_{1}^{2}+y_{1}^{2}=1/2=x_{2}^{2}+y_{2}^{2}.}$

To ukazuje, že v R⁴ Cliffordův torus je podvarietou jednotkové 3-sféry S³.

je snadné ověřit, že Cliffordův torus je minimálním povrchem v S³.

Je také běžné uvažovat Cliffordův torus jako vložený torus v C². Ve dvou kopiích C máme následující jednotkovou kružnici (stále parametrizovanovou úhlem souřadnic):

${\displaystyle S^{1}=\{e^{i\theta }\mid 0\leq \theta <2\pi \}}$

a

${\displaystyle S^{1}=\{e^{i\varphi }\mid 0\leq \varphi <2\pi \}.}$

Nyní Cliffordův torus se objevuje jako

${\displaystyle {\tfrac {1}{\sqrt {2}}}S^{1}\times {\tfrac {1}{\sqrt {2}}}S^{1}=\{{\tfrac {1}{\sqrt {2}}}(e^{i\theta },e^{i\varphi })\,|\,0\leq \theta <2\pi ,0\leq \varphi <2\pi \}.}$

Stejně jako výše jde o vloženou podvarietu v jednotková kouli S³ v C².

Pokud C² popisuje vztah souřadnic (z₁, z₂), pak Cliffordův torus popisuje vztah

${\displaystyle \left|z_{1}\right|^{2}=1/2=\left|z_{2}\right|^{2}.}$

Podle výše uvedené definice je vzdálenost jakéhokoli bodu Cliffordova toru od počátku souřadnicového systému C²

${\displaystyle {\sqrt {{\frac {1}{2}}\left|e^{i\theta }\right|^{2}+{\frac {1}{2}}\left|e^{i\varphi }\right|^{2}}}=1.}$

Množina všech bodů ve vzdálenost 1 od počátku souřadnicového systému C² je jednotka 3-sféry a tak Cliffordův torus vložený do této 3-sféry. Cliffordův torus totiž dělí tuto 3-sféru na dva shodné pevné tory (viz Heegaardovo rozdělení^[2]).

Protože O(4) je akcí na R⁴ při ortogonálních transformacích, můžeme rigidní rotací přeměnit „standardní“ Cliffordův torus definovaný výše na jiné ekvivalentní tory, které všechny nazýváme „Cliffordův torus“. Šestirozměrná grupa O(4) je tranzitivní akcí na prostoru všech takových Cliffordových torů vložený do 3-sféry. Tato akce má však dvourozměrný stabilizátor (viz akce grupy na množině) protože rotace v meridionální a délkovém směru toru zachovává torus (jako protiklad k se šíří ono na různé/jiný/odlišný torus). Tudíž, existuje skutečně čtyřrozměrný prostor Cliffordových torů.^[2] Existuje totiž vzájemně jednoznačná korespondence mezi Cliffordovými tory v jednotkové 3-sféry a dvojicemi polárních hlavních kružnic (tj. hlavních kružnic, které jsou maximálně oddělené). Je-li dán Cliffordův torus, související/příslušnými polární hlavní kružnice jsou core kružnice každého z dva komplementární oblasti. Naopak, pro jakoukoli dvojici polárních hlavních kružnic, související/příslušnými Cliffordův torus je geometrické místo bodů bodů 3-sféry, které jsou stejně vzdálené od obou kružnic.

Ploché tory v jednotkové 3-sféry S³, které jsou součinem kružnic o poloměru r ve stejné 2-rovině R² a poloměru ${\displaystyle {\sqrt {1-r^{2}}}}$ v jiné 2-rovině R² se také někdy nazývají „Cliffordovy tory“.

Na tytéž kružnice můžeme pohlížet jako že mají poloměry, které jsou cos(θ) a sin(θ) pro nějaký úhel θ v intervalu 0 ≤ θ ≤ π/2 (kam zahrnujeme degenerované případy θ = 0 a θ = π/2).

Sjednocení pro 0 ≤ θ ≤ π/2 všech těchto torů tvaru

${\displaystyle T_{\theta }=S(\cos \theta )\times S(\sin \theta )}$

(kde S(r) označuje kružnice v rovina R² definovaný vztahem mající střed (0, 0) a poloměr r) je 3-sféra S³. (Pamatujte, že musíme zahrnout dva degenerované případy θ = 0 a θ = π/2, z nichž každý odpovídá hlavní kružnici S³ a který současně dává dvojici polárních hlavních kružnic.)

Lze hned vidět, že aby tento torus T_θ měl plochu

${\displaystyle \operatorname {area} (T_{\theta })=4\pi ^{2}\cos \theta \sin \theta =2\pi ^{2}\sin 2\theta ,}$

pak pouze torus T_π/4 má maximální možnou plochu 2π². Tento torus T_π/4 je torus T_θ, který se nejčastěji nazývá „Cliffordův torus“ – a je také jediným z T_θ, který je minimálním povrchem v S³.

Jakákoli jednotková koule S²ⁿ⁻¹ v eukleidovském prostor sudé dimenze R²ⁿ = Cⁿ může být vyjádřena pomocí komplexních souřadnic takto:

${\displaystyle S^{2n-1}=\{(z_{1},\ldots ,z_{n})\in \mathbf {C} ^{n}:|z_{1}|^{2}+\cdots +|z_{n}|^{2}=1\}.}$

Pak, pro jakákoli nezáporná čísla r₁, ..., r_n tak, že r₁² + ... + r_n² = 1, můžeme definovat zobecněný Cliffordův torus takto:

${\displaystyle T_{r_{1},\ldots ,r_{n}}=\{(z_{1},\ldots ,z_{n})\in \mathbf {C} ^{n}:|z_{k}|=r_{k},~1\leqslant k\leqslant n\}.}$

Tyto zobecněné Cliffordovy tory jsou vesměs disjunktní. Můžeme jednou opět dojít k závěru, že sjednocení každého jeden těchto torů T_{r1, ..., rn} je jednotka (2n − 1)-koule S²ⁿ⁻¹ (kam musíme opět zahrnout degenerované případy, kde alespoň jeden z poloměrů r_k = 0).

• Cliffordův torus je „plochý“; může být narovnán do roviny bez napnutí, na rozdíl od standardního rotačního toru.
• Cliffordův torus dělí 3-sféru na dva shodné pevné tory. (Ve stereografické projekci se Cliffordův torus objevuje jako standardní rotační torus. Fakt, že dělí 3-sféru stejně znamená, že vnitřek promítnutého toru je ekvivalentní s vnějškem, což nelze snadno vizualizovat).

V symplektické geometrii je Cliffordův torus příkladem vložené symplektické variety C² se standardní symplektickou strukturou. (Samozřejmě jakýkoli součin vložené kružnice v C dává Lagrangovský torus C², takže to nemusí být Cliffordovy tory.)

Hsiangova–Lawsonova domněnka tvrdí, že každý torus minimálně vložený do 3-sféry s round metric musí být Cliffordův torus. Tuto domněnku dokázal Simon Brendle v roce 2012.

Cliffordovy tory a jejich obrazy při konformní transformaci jsou globální minimalizátory Willmorova funkcionálu.

V tomto článku byl použit překlad textu z článku Clifford torus na anglické Wikipedii.

• Duocylinder
• Hopf fibration
• Clifford parallel a Cliffordův povrch
• William Kingdon Clifford