Collatzův problém

Collatzův fraktál, který vznikne rozšířením Collatzovy funkce do spojité komplexní roviny.

Collatzův problém je v matematice domněnka, kterou vyslovil Lothar Collatz. Tento problém je rovněž známý pod názvy 3n + 1 problém, Ulamův problém (podle Stanisława Ulama), Kakutanův problém (podle Šizua Kakutaniho), Thwaitův problém (podle sira Bryana Thwaitese), Hassův algoritmus (podle Helmuta Hasseho) nebo také jako Syrakuský problém^[1]^{[pozn. 1]}. Posloupnost takto zkoumaných čísel se někdy nazývá též jako posloupnost ledové kroupy (protože hodnota čísel v posloupnosti často mnohokrát klesne a opět se zvýší, podobně jako ledové kroupy mění svoji výšku, když dochází k jejich tvorbě v oblacích)^[3]^[4].

Domněnka může být shrnuta následovně. Vezměme jakékoliv kladné celé číslo n. Pokud je n sudým číslem, vydělíme je dvěma, získáme tak n / 2. Pokud je n lichým číslem, vynásobí se třemi a přičte se jednička, tj. 3n + 1. Tento postup (v angličtině nazývaný také „Half Or Triple Plus One“ nebo HOTPO^[5]) se dále opakuje. Domněnka je taková, že nehledě na to, jaké počáteční číslo n je zvoleno – výsledná posloupnost vždy nakonec dojde k číslu 1.

Definice

Popsaný postup lze vyjádřit funkcí

C(n)={\begin{cases}3n+1{\text{,}}&{\text{ je-li }}n{\text{ liché,}}\\n/2{\text{,}}&{\text{ je-li }}n{\text{ sudé.}}\end{cases}}

Hodnota $C(n)$ pro lichá $n$ bude zjevně sudá. Často se tak používá zkrácená varianta a notace modulární aritmetiky

T(n)={\begin{cases}(3n+1)/2{\text{,}}&n\equiv 1{\pmod {2}}{\text{,}}\\n/2{\text{,}}&n\equiv 0{\pmod {2}}{\text{.}}\end{cases}}

Problém pak lze popsat pomocí iterací těchto funkcí: Je pro libovolné počáteční kladné celé číslo $n$ některá $k$ -tá iterace $T^{k}(n)$ rovna jedné? Formálně: $\forall n\exists k.T^{k}(n)=1$ .

Domněnka zatím nebyla dokázána. Byla ale výpočetně ověřena pro všechna čísla až do velikosti 2⁶⁸.^[6]^[7]

Příklad

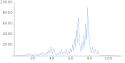
Orbita pro $n=27$ má 111 kroků (41 skrze lichá čísla) a vypadá následovně.

Iterace vystoupaly z čísla 27 až na 9232, přesto se nakonec vrátily k číslu 1.

27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1 ^[8]

Heuristický argument

Heuristický argument^[9] napovídá, že iterace Collatzovy funkce by v dlouhodobém horizontu neměly růst k nekonečnu, ale měly by se naopak zmenšovat.

Pokud je vstup $T(n)$ rovnoměrně rozložený modulo 2, nastávají obě větve $T(n)$ stejně často.

Snadno lze ověřit, že jednotlivé iterace funkce se chovají náhodně a nezávisle od iterací minulých. Přesněji, je-li $n$ rovnoměrně rozložené modulo 4, pak je $T(n)$ rovnoměrně rozložené modulo 2. Pro náhodný vstup tedy nastanou obě větve následující iterace se stejnou pravděpodobností.

Díky tomu lze uvažovat následovně. Pro dostatečně náhodný vstup $n$ bude výstup jedné iterace $T(n)$ zhruba $3n/2$ v první polovině případů a $n/2$ ve druhé polovině případů. Tedy oba případy mají pravděpodobnost 1/2. Přírůstek jedné iterace $T(n)$ v $\log(n)$ lze tedy vyjádřit jako

{\frac {1}{2}}\log {\frac {3}{2}}+{\frac {1}{2}}\log {\frac {1}{2}}<0

.

A protože přírůstek je záporný, lze očekávat, že iterace se budou v dlouhodobém horizontu zmenšovat.

Empirická data

Následující tabulka ukazuje maximální a průměrné délky trajektorií před dosažením jedničky pro počáteční hodnoty do dané velikosti. U maximální délky je uvedena také odpovídající počáteční hodnota.

hodnoty pod	maximální délka	počáteční hodnota	průměrná délka
$10^{1}$	$19$	$9$	$6{,}78$
$10^{2}$	$118$	$97$	$31{,}48$
$10^{3}$	$178$	$871$	$59{,}49$
$10^{4}$	$261$	$6\,171$	$84{,}97$
$10^{5}$	$350$	$77\,031$	$107{,}54$
$10^{6}$	$524$	$837\,799$	$131{,}43$
$10^{7}$	$685$	$8\,400\,511$	$155{,}27$
$10^{8}$	$949$	$63\,728\,127$	$179{,}23$
$10^{9}$	$986$	$670\,617\,279$	$203{,}23$
$10^{10}$	$1\,132$	$9\,780\,657\,630$	$227{,}25$

Odkazy

Poznámky

↑ Název „Syrakuský problém“ navrhl Hasse v 50. letech 20. století při návštěvě na Syracuse University.^[2]

Reference

V tomto článku byl použit překlad textu z článku Collatz conjecture na anglické Wikipedii.

↑ MADDUX, Cleborne D.; JOHNSON, D. LAMONT. Logo: A Retrospective. New York: Haworth Press, 1997. ISBN 0-7890-0374-0. S. 160. (anglicky)
↑ LAGARIAS, Jeffrey C. The 3x + 1 problem and its generalizations. The American Mathematical Monthly. 1985, s. 3–23. JSTOR 2322189. (anglicky)
↑ PICKOVER, Clifford A. Wonders of Numbers. Oxford: Oxford University Press, 2001. ISBN 0-19-513342-0. S. 116–118. (anglicky)
↑ Hailstone Number [online]. Wolfram Research. Dostupné online. (anglicky)
↑ FRIENDLY, Michael. Advanced Logo: A Language for Learning. Hillsdale NJ: Lawrence Erlbaum Associates, 1988. ISBN 0-89859-933-4. (anglicky)
↑ Barina, D. Convergence verification of the Collatz problem. J Supercomput (2020). https://doi.org/10.1007/s11227-020-03368-x
↑ https://math.stackexchange.com/a/3316195/204448
↑ Posloupnost A008884 v databázi On-Line Encyclopedia of Integer Sequences
↑ https://terrytao.wordpress.com/2011/08/25/the-collatz-conjecture-littlewood-offord-theory-and-powers-of-2-and-3/

Literatura

The Ultimate Challenge: The $3x+1$ Problem. Příprava vydání Jeffrey C. Lagarias. [s.l.]: American Mathematical Society, 2010. Dostupné online. ISBN 978-0-8218-4940-8.

Externí odkazy

Obrázky, zvuky či videa k tématu Collatzův problém na Wikimedia Commons
3x+1 problem – v encyklopedii On-Line Encyclopedia of Integer Sequences
Collatz Problem – v encyklopedii MathWorld

[Syracuse-3] Název „Syrakuský problém“ navrhl Hasse v 50. letech 20. století při návštěvě na Syracuse University.^[2]

[1] MADDUX, Cleborne D.; JOHNSON, D. LAMONT. Logo: A Retrospective. New York: Haworth Press, 1997. ISBN 0-7890-0374-0. S. 160. (anglicky)

[Lagarias_(1985)-2] LAGARIAS, Jeffrey C. The 3x + 1 problem and its generalizations. The American Mathematical Monthly. 1985, s. 3–23. JSTOR 2322189. (anglicky)

[4] PICKOVER, Clifford A. Wonders of Numbers. Oxford: Oxford University Press, 2001. ISBN 0-19-513342-0. S. 116–118. (anglicky)

[hn-5] Hailstone Number [online]. Wolfram Research. Dostupné online. (anglicky)

[6] FRIENDLY, Michael. Advanced Logo: A Language for Learning. Hillsdale NJ: Lawrence Erlbaum Associates, 1988. ISBN 0-89859-933-4. (anglicky)

[7] Barina, D. Convergence verification of the Collatz problem. J Supercomput (2020). https://doi.org/10.1007/s11227-020-03368-x

[8] ttps://math.stackexchange.com/a/3316195/204448

[9] Posloupnost A008884 v databázi On-Line Encyclopedia of Integer Sequences

[10] ttps://terrytao.wordpress.com/2011/08/25/the-collatz-conjecture-littlewood-offord-theory-and-powers-of-2-and-3/

[1]

[pozn. 1]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[2]

Navigation

Navigace

Tématické portály