Dějiny matematiky

Dějiny matematiky, také základní rysy vývoje matematiky od prehistorie po dnešek, postihují období několika tisíciletí. Dlouho předtím, než se matematika vyvinula jako samostatná oblast znalostí, se lidé zabývali čísly, strukturami, tvary a čísly, umístěním v prostoru a dalšími tématy souvisejícími s matematikou. Nejzákladnějším matematickým procesem je počítání, je tedy přirozené začít historii matematiky čísly a číselnými systémy. Na začátku bylo třeba být schopen měřit, vážit a být schopen porovnávat různé velikosti. Od primitivního počítání a měření se matematika postupně vyvinula do více obecných a abstraktních myšlenek a teorií.

Nejstarší matematické texty, které známe, pocházejí ze starověké Mezopotámie z doby kolem roku 1800 př. n. l. a ze starověkého Egypta od roku 1650 př. n. l. Také v Indii byly nalezeny staré matematické texty z let 800 až 500 př. n. l. Nejstarší texty pojednávají o problémech a metodách aritmetiky a geometrie, ve všech třech zemích měl člověk znalosti o tom, co se dnes označuje jako Pythagorova věta. Z Číny známe také velmi staré matematické texty.

Základ pro matematiku jako samostatný obor byl položen ve starověkém Řecku. V 6. století před naším letopočtem Pythagoras a jeho učedníci propojili matematiku, hudbu a mystiku ve škole, kde byla znalost čísel a geometrie základní. Eukleidés žil v Alexandrii kolem roku 300 př. n. l. a svým axiomatickým přístupem se Eukleidovy prvky staly důležitou učebnicí po tisíce let. Také Archimédés (nar. kolem 287 př. n. l.) měl ve středověku velký význam pro pozdější vědu. Znalosti řecké matematiky byly v Evropě do značné míry zapomenuty, ale byly zachovány a dále rozvíjeny v muslimském světě, v Arábii a Persii. Ve středověku byly arabské texty přeloženy do latiny a tyto překlady přenesly do Evropy znalosti řecké, arabské a indické matematiky. Neméně důležité bylo zavedení hindsko-arabských číslic do Evropy ve 13. století.

Vývoj matematiky v evropském středověku byl pomalý, ale byl stimulován založením prvních univerzit. Zatímco Řekové ve starověku se vyhýbali nekonečným procesům, evropští matematici v 15. století studovali nekonečné důsledky a posloupnosti. Vzhledem k potřebám navigace se trigonometrie stala stále důležitější součástí matematiky. François Viète (1540–1603) představil použití písmen v rovnicích a položil tak základ moderní matematické notaci.

Matematika byla vždy důležitým nástrojem přírodních věd a pokroky v matematice se téměř vždy shodovaly s vývojem v jiných předmětech, v neposlední řadě ve fyzice a astronomii.

K rozvoji matematiky přispělo také mnoho přírodovědců, například Galileo Galilei (1564–1642) a Johannes Kepler (1571–1630).

Zásadní význam pro rozvoj v 18. století bylo zavedení analytické geometrie René Descartesem (1596–1650) a Pierre de Fermatem (1607–1665). Mezníkem bylo také zřízení diferenciálního a integrálního počtu, kde základ položili Gottfried Leibniz (1646–1716) a Isaac Newton (1642–1726). Koncept funkce vznikl při studiu geometrických křivek a rovnic. Byla zavedena postupná standardizace matematické notace, v neposlední řadě ovlivněna pracemi Leibnize a Leonharda Eulera (1707–1783). Studium algebraických rovnic v 17. století vedlo k zavedení komplexních čísel, což je důležitý krok v procesu, kdy se matematické veličiny stávají stále abstraktnějšími. Použití této formy čísel bralo vážně práci Leonharda Eulera a vytvoření komplexní funkční analýzy Augustinem Louisem Cauchyem (1789–1857). Carl Friedrich Gauss (1777–1855), snad vůbec největší matematik, dokázal mimo jiné základní teorém v algebře o existenci komplexních kořenů v polynomiální rovnici. Objev, že je možné definovat neeuklidovské geometrie, přiměl mnoho lidí dívat se na základ matematiky novýma očima. Zkoumání patologických funkcí také ukázalo, že mnoho intuitivních konceptů vyžaduje jasnější objasnění. V 19. a 20. století mnoho matematiků pracovalo na vytvoření přísného základu pro matematiku. Karl Weierstrass (1815–1897) byl ústřední postavou v procesu objasňování rozdílu mezi geometrií a algebrou, v procesu, který se od té doby nazývá „aritmetizace analýzy“. Teorie množin zavedená Georgem Cantorem (1845–1918) položila základ pro nový způsob vyjadřování, který se dnes používá téměř ve všech částech matematiky. Studium matematických struktur, jako jsou skupiny, metrické prostory a vektorové prostory, bylo důležité pro vývoj abstraktní algebry.

V roce 1900 vytvořil David Hilbert (1862–1943) seznam 23 nevyřešených matematických problémů, které měly velký vliv na vývoj současné matematiky. Výzvou bylo dokázat, že axiomy aritmetiky jsou konzistentní. Ideální obraz dokonalého matematického systému byl ve 20. století občas narušen, v neposlední řadě, když Kurt Gödel (1906–1978) ukázal, že není možné definovat formální axiomatický systém jako základ pro celou matematiku.

Druhá polovina 20. století je období, které se charakteristice zobecňování prostorových a kvantitativních vztahů dostatečně nevymyká, jde-li o předmět matematiky, ale v metodách je značně ovlivněno informatikou, kybernetikou, teorií her apod. Matematika se nadále rozvíjí jak do šířky, tak do hloubky a předmět je dnes tak rozsáhlý, že je nemožné mít přehled o všem.

Americký historik matematiky Morris Kline v knize Matematika ztráta určitosti (1980) říká: "Hlavní příčinou rozvoje matematiky je její použití ke studiu přírody. Matematické pojmy i matematické metody poznání, jsou nejúčinnějším prostředkem výzkumu a vysvětlení nebeských těles, pohybu těles na Zemi a v její blízkosti, světelných, zvukových, tepelných a elektrických jevů, elektromagnetických vln, stavby hmoty, chemických reakcí, stavby oka, ucha i jiných orgánů lidského těla a mnoha set jiných důležitých jevů." ^[1]

Původ matematiky spočívá v lidské potřebě umět počítat, umět měřit a umět popsat velikost a tvar. Ve všech raných společnostech lovců a sběračů bylo důležité umět sdělit čísla, jako je počet zvířat a počet nepřátel. Struktura v několika jazycích může naznačovat, že první formy primitivního počítání byly založeny na rozdílu mezi „jednou“, „dvěma“ a „mnoha“. Uvědomění si, že dva kameny a dvě ryby mají něco společného, představuje první formu abstrakce, která je v matematice zásadní. Tělo bylo dlouho používáno jako pomůcka a Aristoteles poznamenal, že počítání na základě pěti a deseti je přímým důsledkem počtu prstů na rukou a nohou. Anglické slovo „digit“ pro čísla pochází z latiny „digitus“, což znamená „prst“. Také mnoho jmen primitivních měrných jednotek ukazuje původ v těle, například vztahující se k délce ruky, nohy a paže. Archeologické vykopávky v Československu odhalily stehenní kost od vlka datovaného kolem roku 30 000 př. n. l. Na této kosti bylo vyryto 55 řádků, systematicky jeden po druhém. Počítání primitivů bylo založeno na kreslení čar a možná také na porovnání s řadou tyčí, kamenů a podobně. Bylo nutné mít dobře vypracovaný kalendář, aby člověk věděl, kdy je čas zasít a sklízet. K vytvoření kalendáře byly kromě znalostí čísel a aritmetiky zapotřebí rozsáhlé astronomické znalosti. Znalosti v astronomii jsou rozvíjeny matematickými výpočty. Zemědělské společenství musí být rovněž schopno provádět zeměměřičství, aby bylo možné rozdělit země mezi rolníky. Zeměměřičství vyžaduje geometrické znalosti a slovo „geometrie“ pak také znamená zeměměřičství. Bylo potřeba zmapovat a vypočítat pravidelné povodně, aby se člověk mohl chránit před nadměrnými ztrátami plodin a lidským životem. Po povodni se často muselo znovu měřit plochy půdy zemědělců, protože povodně často vedly ke změnám v krajině. Historické prameny ukazují, že všechny civilizace vyvinuly matematické znalosti k řešení praktických problémů týkajících se účetnictví, astronomie, zemědělství a stavebnictví. Vznik prvních matematických pojmů spadá do oblastí nejstarších říčních kultur (Egypt, Mezopotámie, Čína, Indie). První souvislé matematické texty, jež se dochovaly, pocházejí z Egypta a Mezopotámie z přelomu 3. a 2. tisíciletí př. n. l. Předcházelo jim dlouhé období formování pojmů, které se v těchto textech vyskytují. O tomto období však nemáme žádné písemné doklady a jen velmi málo dokladů hmotných.^[2]

Počáteční období, v němž se vytvářely kvantitativní a geometrické vztahy a operace s nimi, trvalo velmi dlouho. Až do 6. století př. n. l. šlo převážně o hromadění aritmetických pojmů, geometrických faktů a základních operací. Matematické znalosti se zaznamenávaly pouze různými systémy číslic a běžným jazykem, což brzdilo rychlejší rozvoj. Do 3. století př. n. l. chybí matematice jakákoliv speciální symbolika.

viz článek Matematika starověkého Egypta

Matematika starověkého Egypta vznikala společně s rozvojem civilizace od 4. tisíciletí p. n. l. Egypťané používali základní operace sčítání, odčítání, násobení (převáděli na opakované sčítání), dělení. Počítali se zlomky, řešili aritmetické a geometrické úkoly (nap. trojčlenku a rovnice o jedné neznámé). Své znalosti užívali převážně k praktickým účelům. Úvodem do geometrie se staly práce s vyměřováním pozemků (jejich hranice byly každoročně narušovány povodněmi Nilu a bylo nutno je obnovovat). Uměli vytyčit pravý úhel (pomocí provazu o délkách 3, 4 a 5 jednotek), pro určení ostrých úhlů měli tabulky (lze říci, že znali funkci „kotangens“). Znali konstantu ${\displaystyle \pi }$ pro stanovení obsahu a obvodu kruhu (s odchylkou méně než 1 %). Většinu znalostí o egyptské matematice poskytl tzv. Rhindův papyrus (z období před rokem 1650 př. n. l.) a asi o dvě století starší Moskevský papyrus.

Rhindův papyrus je nejrozsáhlejší a nejvýznamnější matematický text ze starého Egypta, byl opsán kolem roku 1560 př. Kr. písařem Ahmosem z materiálu pocházejícího z doby vlády Amenemheta III. (asi 1853 až 1809). Obsahuje 87 úloh s návody a řešeními a dvě tabulky, ve kterých jsou různé zlomky zapsány jako součet kmenových zlomků (zlomek je zapsán jako součet zlomků s čitatelem 1).^[3]

Moskevský papyrus (asi 1890 př. n. l.) je starší než papyrus Rhindův, ale není tak bohatý na obsah. Papyrus obsahuje 25 matematických problémů a řešení jednoho z těchto problémů ukazuje, že Egypťané mohli vypočítat objem komolého kužele, tj. zkrácené pyramidy. Další problém se týká výpočtu plochy zakřiveného povrchu, ale text uvádí nejednoznačný popis dotyčného povrchu.

Egyptský zápis čísel je jeden z nejstarších, používali desítkový početní systém a nepoziční číselnou soustavu (nezáleží na pořadí, v jakém jsou znaky uspořádány).^[4]

Z Mezopotámie (dnešní Irák) pocházejí první písemné památky v dějinách lidstva z období 2200 až 1800 př. n. l. Znalosti o starověkých Mezopotámcích a sumerských kulturách pocházejí z velmi bohaté sbírky hliněných tabulek s klínovým písmem. Tabulky s matematickými znalostmi pocházejí ze dvou časových období, většina z nich pochází ze starobabyllonského období (1900–1600 př. n. l.), ale některé ze Seleucidské říše (323–60 př. n. l.). V druhé polovině 19. století a především ve 20. století se výzkumu a studiu zápisů na těchto tabulkách věnovala řada vědců. Edward Hincks studoval texty, vztahující se k asyrské epose, které obsahovaly astronomické tabulky. Ukázal, že se zde používala šedesátková soustava. Francouzská expedice (1894 až 1895) objevila archív ve starosumerské Lagaši který obsahoval mimo jiné i hospodářské zápisy, plány, výpočty obsahů polí apod.

Roku 1900 byly publikovány matematické tabulky z Nippuru obsahující soubory tabulek pro násobení a dělení a tabulky druhých a třetích mocnin. Na počátku 20. století bylo v Nippuru objeveno více než 80 matematických tabulek a o něco později asi 50 matematických tabulek ve městě Kiš.^[5] Německý matematik a historik Oskar Neugebauer (1899–1990) překládal klínopisné texty o v letech 1935 až 1937 vydal své stěžejní trojsvazkové dílo Mathematische Keilschrift- Texte, v němž publikoval matematické klínopisné texty asi 250 tabulek. Na základě všech těchto poznatků byly v padesátých a šedesátých letech 20. století vydávány monografie, které popisovaly úroveň sumerské, starobabylónské a novobabylónské matematiky, jejichž autory byli např. E. M. Bruins, A. E. Rajk, I. N. Veselovskij, K. Vogel, Mark Jakovlevič Vygodskij (1898–1965) a Bartel L. van der Waerden (1903–1996).

Systémy nepozičního zápisu čísel (např. jednotka byla zaznamenávána jako otisk malého kužele, deset malých kuželů byl jeden malý kruh, šest malých kruhů byl jeden velký kužel, deset velkých kuželů byl jeden velký kužel s kruhem uvnitř, atd., v této soustavě, která byla založena na kombinaci dvou soustav o základech 10 a 6, se obyčejně zapisovala čísla od 1 do 360000) vydržel do poloviny třetího tisíciletí, kdy byl postupně nahrazován pokročilejším akkadským zápisem založeným na „poziční" soustavě o základu 60. Chaldejští počtáři světu zanechali šedesátkovou soustavu (čas, úhly), rozdělení kruhu na 360 stupňů, dne na 24 hodin, hodiny na 60 minut a minuty na 60 sekund. Matematika pracovala pouze s přirozenými čísly, kladnými šedesátinnými zlomky a smíšenými čísly. K početním operacím (sčítání, odčítání, násobení, dělení) se používali tabulky např. převrácených hodnot, tabulky druhých a třetích mocnin (také druhých a třetích odmocnin) přirozených čísel a tabulka jejich součtů. Uplatňovaly se při řešení úloh, které dnes řešíme pomocí kvadratických nebo kubických rovnic. Jiné tabulky obsahovaly různé charakteristiky trojúhelníků a pravidelných n-úhelníků, různé „technické koeficienty", převody jednotek atd. Soubor měr a vah byl relativně standardizovaný; pevné stanovené relace mezi jednotkami, většina převodů pracuje jen s jednoduchými šedesátinnými zlomky. Zachovalo se několik tabulek, které obsahují příklady vedoucí na aritmetickou (dělení majetku) i geometrickou posloupnost.

Babylóňané vyvinuli také postupy pro řešení matematických problémů. Byli dobře obeznámeni s lineárními i kvadratickými rovnicemi a v mnoha případech také dokázali redukovat algebraické rovnice vyššího řádu na kvadratické rovnice. Vyvinuli metodu pro hledání přibližných výrazů pro odmocniny. Pomocí zlomkových výrazů se například podařilo vyjádřit kořen 2 jako, s chybou kolem 0,000008! Nejslavnější babylonská hliněná deska byla pojmenována Plimpton 322, vyrobená kolem roku 1800 před naším letopočtem. Hliněná deska obsahuje mimo jiné tabulku Pythagorových trojic, tj. tří čísel který splňuje rovnici. Babyloňané znali Pytagorovu větu více než tisíc let před tím, než Pytagoras žil. Organizace pythagorovských trojic na desce může také naznačovat časnou formu trigonometrie.^[5] Babyloňané byli tradičně zobrazováni jako průkopníci algebry a Egypťané jako zakladatelé geometrie. Mnoho tabulek klínového písma však ukazuje, že Babyloňané byli v geometrii stejně vyspělí jako Egypťané.

Indická matematika byla ve své době obdivuhodně rozvinutá. Světu přinesla především poziční systém. Existovaly symboly pro prvních devět číslic. Desítkový charakter byl velmi rozvinutý. To vše byly příznivé podmínky pro vytvoření poziční soustavy se základem 10. Obrovským objevem indických matematiků se stala nula: 0. Se způsobem zápisu čísel velmi úzce souvisí provádění základních aritmetických operací – sčítání, odčítání, násobení a dělení. Staří Indové mezi ně řadili výpočet druhé a třetí mocniny, druhé a třetí odmocniny a některé algoritmy. Považují se za algebraické (např. pravidlo tří, tj. trojčlenka, metoda falešného předpokladu, směšovací počet, úrokový počet). Podstatnou součástí indické aritmetiky bylo počítání se zlomky. Nejstarší indické geometrické znalosti jsou obsaženy v textech zvaných šulbasútry neboli pravidla provazce (1. tisíciletí př. n. l.), v nichž jsou uvedena nejdůležitější pravidla používaná při stavbě obětních oltářů. Kolem počátku našeho letopočtu byla výrazným impulzem džinistická kosmologie, která používala při výpočtech velká čísla (úvahy o nekonečnu).

Také se rozvíjela kombinatorika; např. prozodik Pingala (kolem roku 200 př. n. l.) popsal schéma binomických koeficientů, které dnes známe jako Pascalův trojúhelník. Největších úspěchů dosáhli indičtí matematici v algebře (6. do 14. století). Již tehdy zahrnovala operace se zápornými čísly a počítání s čísli iracionálními. Hlavním tématem bylo řešení slovních úloh, (rovnicí s jednou neznámou nebo rovnicemi s více neznámými). Indičtí učenci formulovali pravidla pro řešení lineárních a kvadratických rovnic a jejich soustav, zabývali se rovněž některými rovnicemi vyšších stupňů a zejména neurčitými rovnicemi. Metodu kuttaka užívali k řešení neurčité lineární rovnice se dvěma neznámými (tj. tzv. diofantická rovnice) a algoritmus pro řešení tzv. Pellovy rovnice. Neměli k dispozici názornou a propracovanou symboliku; používali zkratky slov, strany rovnic zapisovali pod sebou, algoritmy popisovali slovně a dokladovali je na konkrétních příkladech. Ovládali počítání se zlomky, jejich forma se téměř shodovala se současnou: čitatele psali nad jmenovatelem, nepoužívali zlomkovou čáru. Při operacích s celými čísly a se zlomky vyjadřovali celá čísla jako zlomky se jmenovatelem 1. Umocňovali dvěma a třemi, znali a používali trojčlenku a mnoho dalšího.^[6]

Řekové významně přispěli k rozvoji matematiky. Ve druhé polovině 4. stol. př. n. l., ještě před Eukleidem, napsal Aristotelův žák Eudémos z Rhodu Dějiny matematiky, Dějiny geometrie a Dějiny astronomie. Tato díla byla bohužel ztracena. Rozvíjelo se logické uvažování, nejznámější knihou napsanou na tomto základě, se staly Euklidovy Základy (řecky Stoicheia, latinsky Elementa) ze 3. století př. n. l. Euklides shromáždil všechny znalosti té doby z matematiky. Tato práce obsahuje nejen geometrii, ale jsou zde shrnuty všechny výsledky bádání z této doby v oblasti matematiky. Na vznik matematických pojmů a operací s nimi, působily praktické podněty (obchod, peněžnictví, zeměměřičství, mořeplavby, astronomie…).^[7]

Pythagoras ze Samu považoval za základ číslo, bod (bod jako prvek nejmenší vymezenosti – jeden bod je bod, dva body jsou úsečka, tři body tvoří trojúhelník, čtyři body prostorové těleso a součet těchto čísel dává číslo deset, které považoval za magickou konstrukci vesmíru). Velkou pozornost věnoval geometrii viz Pythagorova věta. Přívrženci jeho filozofie se nazývají pythagorejci, šlo o řecké filozofy, obývající řecké osady na jihu Itálie a příslušníky Pythagorovy školy. Pythagorejci prosazovali studium tzv, kvadrivia, které sestávalo z geometrie, aritmetiky, astronomie a hudby. Toto pojetí se zachovalo až do přelomu středověku a novověku, kdy bylo studováno na prvních univerzitách (na fakultách sedmi svobodných umění) vedle tzv. trivia (gramatika, rétorika, dialektika). Eukleidés se narodil v Řecku, o jeho životě je známo málo. Studoval snad v Athénách na Platónově Akademii, kde se geometrii naučil od Eudoxa a Theaitéta. Král Ptolemaios I. (323 – 283 př. n. l.) ho povolal do nově založené Alexandrijské knihovny. Mezi jeho žáky patřil snad i Archimédés.

(c) Fondazione Cariplo, CC BY-SA 3.0

Eukleidovo dílo patří k nejvýznamnějším, jsou to třináctidílné Základy (Stoicheia) založené na systému ústředních axiomů geometrie, které další dva tisíce let určovaly evropské geometrické myšlení. Podává v nich také důkaz Pythagorovy věty a důkaz nekonečného množství prvočísel. Archimédés patří mezi nejvýznamnější učence antiky. Objevil mnoho zákonů matematiky a fyziky. V geometrii zavedl původně negeometrické pojmy jako těžiště, těžnice. Věnoval se metodám výpočtu ploch (především kruhu, elipsy a parabolické úseče) a objemů těles (zejména válce, kužele, koule, elipsoidu,paraboloidu). Sestrojil nekonečnou posloupnost trojúhelníků (první známý příklad součtu nekonečné řady). Své matematické výzkumy shrnul ve spise „De mechanicis propositionubis ad Eratosthenes methodus“ (O metodě mechanicky odvoditelných vět), Tato teorie byla objevena až v roce 1906. Odvodil obvod a obsah kruhu. (Podrobněji viz článek Archimédés). Základy moderního matematického myšlení lze nalézt u Zena z Elea, který je známý svými paradoxy. Řečtí matematici považovali problematiku "proslulých úloh" za velmi závažnou. Např. v 5. století př. n. l. filozof Anaxagorás z Klazomen si prý úvahami o kvadratuře kruhu krátil dlouhou chvíli ve vězení. Antifón z Athén počítal obsah kruhu pomocí vepsaných pravidelných n-úhelníků (n = 4, 8,16). Hippokratés z Chiu byl jónský filozof a matematik, učil v Athénách. Sepsal matematické pojednání Stoicheia, které se snad stalo vzorem prvních čtyř knih Eukleidova stejně nazvaného spisu. Hippiás z Élidy byl matematik a astronom. Byl i znalcem literatury, hudby a historie, ovládal i některá řemesla. Archytás z Tarentu (428?-365) byl pythagorejský filozof a matematik, státník a vojevůdce. Byl přítelem Platóna, učitelem Eudoxa. Připisují se mu výsledky týkající se poměrů a úměr, formulování zákonů harmonie, vynález kladky a šroubu. Někdy se uvažuje, že je autorem osmé knihy Eukleidových Základů. Lze zmínit i matematika Dinóstratose (4. stol. př. n. l. – také žák Platóna a Eudoxa) nebo Menaechmose. Na základě Menaechmových úvah, vymyslel prý Platón mechanický nástroj pro nalezení dvou neznámých hodnot (speciální příložníky – tesařské úhelníky, zasunovatelné do sebe). Proslulými úlohami se i v dalším období zabývala řada řeckých matematiků. Následující výčet není jistě úplný: Eratosthenés z Kyrény, Diokles (kolem r. 200 př. n. l.) studoval problém konstrukce dvou geometrických úměrných a nalezl křivku kisoidy. Nikomédes pro řešení problémů trisekce úhlu a zdvojení krychle užíval křivku konchoidu nebo Pappos, ten je známý díky svému dílu Synagogé a Pappově větě.^[7]

Staří Číňané byli znamenití počtáři, což dokazuje nejen množství unikátních astronomických výpočtů (např. předpovědi zatmění Slunce) nebo zavedení vlastního lunisolárního kalendáře. Nejstarší dochované zdroje čínské matematiky pocházejí z čísel vyrytých na skořápkách želv. Ty pocházejí z dynastie Šang (asi 1 500–1027 př. n. l.). Tato čísla se zapisují do pozičního systému tak, že číslo 123 se zapisuje (shora dolů) se symbolem pro 1 一 následovaným symbolem pro 100 百, poté symbolem pro 2 二 následovaným symbolem pro 10 十, a nakonec symbol pro 3:（společně 一百 二十 三). Tento číselný systém se kromě arabských čísel stále používá v čínském psaném jazyce. Rychlé a pokročilé výpočty lze provádět pomocí suànpánu , což je čínské počítadlo. Tento vynález byl pravděpodobně vyvinut pro praktické použití obchodníky. Základem čínské i japonské matematiky se stala kniha Devět traktátů o matematickém umění pocházející asi z doby 1. tisíciletí př. n. l. Pojednává o kmenových zlomcích a o plochách základních geometrických útvarů. Mezi další matematiky patří Zu CHongzhi, kromě astronomie se věnoval výpočtům kalendáře.

Úvod do studia matematiky a Správné zrcadlo čtyř neznámých matematika Zhu Shije (1265 - 1320) jsou považovány za vrchol klasické čínské matematiky své doby. Zabýval se zlomky a řešením rovnic; věnoval se řešení polynomiální rovnice několika proměnných, součty konečných řad,určil speciální znak pro nulu atd. Jako první matematik v Číně přispěl k zobecnění a k abstrakci matematiky. Další rozvoj čínské matematiky nastal až o několik století později, pod vlivem matematiky evropské.

Arabská matematika byla nejvíce ovlivněna matematikou mezopotámskou, řeckou a indickou. Z indické matematiky převzala zápis čísel a algoritmy pro písemné počítání, z řecké matematiky abstraktní geometrii a myšlenku axiomatické výstavby matematiky, z mezopotámského a egyptského světa převzala tradici numericky náročných výpočtů a především důraz na užití matematiky v praktickém životě.

Nejvýraznějším arabským matematikem byl Muhamad Ibn Músa Al-Chwárízmí. Své práce o řešení rovnic popsal v knize Kitab al-muchtasav min chisáb al-džabr wa-I-mukabala, tak získala algebra své jméno: je odvozeno od slova al-džabr. Chwárízmí vycházel z řecké matematiky a shrnul tehdejší znalosti arabské matematiky. Arabové převzali od Indů trigonometrické funkce sinus a kosinus, které doplnili o funkce tangens a kotangens. Chwárízmí sestavil jedny z prvních trigonometrických tabulek, zabýval se aritmetikou i algebrou (řešení rovnic). Další dochovaná díla: Kniha o algebře, Kniha o vzácných jevech v umění výpočtů a Kniha o vyměřování a geometrii, která sepsal Abú Kámil Šudza (zvaný Hasíb Mistrí) dokazují, že autor byl patrně první matematik, který hledal více řešení daného problému. Z jeho práce čerpal italský matematik Leonard Pisánský zvaný Fibonacci. Perský astronom a matematik Muhamad Abul Vafa zásadním způsobem rozvinul poznání trigonometrie. Na přelomu prvního tisíciletí se arabští učenci věnovali geometrickému řešení kubických rovnic, pomocí aproximací řešili iracionální čísla, řešili úlohy z geometrie, uměli pro přirozené mocniny použít binomickou větu.

V období středověku matematika, stejně jako ostatní vědy, v Evropě upadá. Důležitou středověkou početní pomůckou byl abakus, který používali již staří Řekové, ale jehož znalost byla po pádu římského impéria na dlouhou dobu zapomenuta a byla znovu objevována. Až do 10. století se v Evropě k zápisu čísel používaly pouze římské číslice. Ve 12. století se v Evropě rozšířilo slovo cifra ve smyslu číslice nebo číslo. Rozhodující význam pro přijetí desítkové poziční soustavy a nových číslic měly nové spisy, které se v Evropě šířily (např. Libro alghvarismi de practica arismatrice (Kniha Algorisma o aritmetické praxi) od Joanna Sevillského; Liber ysagogarum Alghorismi in artem astronomicam a magistro A. compositus (Kniha uvedení Algorisma do astronomického uměni) neznámého mistra). Někteří myslitelé a církevní matematici přesto dospěli k jistým důležitým výsledkům. Mikuláš Oresme (druhá polovina 14. století) studoval mocniny s lomenými exponenty, ale především je znám prací, v níž se zabývá závislostí mezi veličinami. Nanáší závisle proměnnou (latitudo — šířku) vůči nezávisle proměnné (longitudo — délce), kterou lze měřit. Je v tom druh přechodu od souřadnic na nebeské nebo zemské sféře (které znali již ve starověku) k moderním geometrickým souřadnicím. Jeho práce o tom byla několikrát vytištěna v letech 1482 až 1515 a pravděpodobně ovlivnila renesanční matematiky včetně Descarta.

Až do poloviny 15. století neexistovaly žádné symboly pro označení aritmetických operací. Byly vyjadřovány pouze slovy nebo z kontextu nebo z vlastního zápisu výpočtu. U zrodu symbolů pro aritmetické operace stál Johannes Wídmann (1462-1498), který ve své knize Behende und hubsche Rechenung auff allen kauffmanschafft (Hbité a pěkné počítání pro všechny kupce) vydané v Lipsku roku 1489 použil symboly + a —; poprvé se tak tyto symboly objevily ve vytištěné knize.^[8]

Johannes Mtiller zvaný Regiomontanus (1436–1476) se již zcela zbavil šedesátinného systému a v roce 1467 sestavil první čistě desetinné trigonomet­rické tabulky (vydané až po jeho smrtí roku 1490). První souhrn vědomostí o zlomcích a operacích s nimi podal nizozemský matematik Simon Stevín (1548–1620) ve své knize Arithmétique (1585).

Do začátku 16. století nebyl učiněn žádný podstatný pokrok k překonání úrovně arabské a antické matematiky.

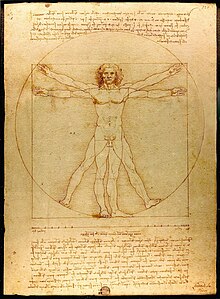
Na počátku 16. století překročila evropská matematika rámec znalostí, které byly vytvořeny v antickém Řecku a národy orientu. První nové a původní výsledky přinesli italští matematici, pracující v oblasti řešení rovnic. Významným matematikem byl Scipione del Ferro (1465–1526), který v roce 1515 nalezl metodu řešení kubických rovnic tvaru ${\displaystyle x^{3}+mx=n.}$. Řešení rovnic 4. stupně odvodil Lodovico Ferrari (1522–1565). Zásadní pokrok učinil geniální samouk Nicollo Tartaglia (1499–1557), který našel obecné řešení kubických rovnic. Řešení kubických rovnic zveřejnil ve své knize Ars magna (Velké umění) v r. 1545 Girolamo Cardano (1501-1576). Tartagliovy výsledky jsou tak dodnes známy pod názvem Cardanovy vzorce. Zmíněná Cardanova kniha je často označována za první knihu moderní matematiky. Francouzský matematik François Viète vybudoval algebru jako učení o algebraických rovnicích. Zabýval se trigonometrií, našel rozvoje funkcí ${\displaystyle cos(nx)}$ a ${\displaystyle sin(nx)}$ v mocninách ${\displaystyle cos(x)}$ a ${\displaystyle sin(x)}$, první vyšetřoval nekonečné součiny. V Matematickém kánonu (1579) uveřejnil tabulky funkcí sinus, kosinus, tangens, kotangens, sekans a kosekans. Roku 1591 vydal In artem analyticam isagoe (Úvod do analytického učení).

René Descartes, jeden ze zakladatelů novověké filozofie a vědy žil po roce 1628 v Nizozemí. V r. 1637 vyšla v Leydenu jeho proslulá Rozprava o metodě ( principy analytické metody a aplikace v matematice a fyzice). Je to první tištěná práce obsahující prvky analytické geometrie (dříve napsaná práce Fermatova zůstala pouze v rukopisu). Descartes se matematikou začal hlouběji zabývat v r. 1618 a dospěl k analogické algebraické symbolice. Zvolil symboly a, b, c,... pro označování koeficientů, x, y, z,... pro označení neznámých. Znovu zformuloval základní větu algebry (před ním A. Girard v r. 1629).

Skotský matematik John Napier popsal podstatu logaritmu nezávisle na švýcarském astronomovi Jostu Bürgovi (ten objevil diferenční počet, jako předchůdce infinitesimálního počtu v oboru celých čísel). Také Henry Briggs pracoval mimo jiné na logaritmech.

V r. 1638 vyšly v holandském Leydenu Galilea Galileiho („otec moderní astronomie“, „otec moderní fyziky“) Rozpravy a matematické důkazy o dvou nových vědách (přinesly výklad jeho mechaniky). Galileo Galilei byl předchůdcem Bonaventura Cavalieriho v matematické analýze, také předchůdcem zakladatelů teorie pravděpodobnosti.

Při řešení problémů mechaniky přinášejí nezávisle na sobě ve druhé polovině 17. století nové matematické prostředky pro zkoumání fyzikálních jevů Gottffried Wilhelm Leibniz a Isaac Newton (infinitezimální počet). Později byl aplikován i v geometrii (Gaspard Monge).

Leonhard Euler, švýcarský vědec a nejvýkonnější matematik 18. století v učebnicích ustálil symboliku algebry a infinitezimálního počtu. Chápání goniometrických funkcí jako poměrů pochází od něho. Sepsal kvalitní učebnice matematické analýzy. Systematicky popsal a rozšířil poznatky o nekonečných řadách, analyticky popsal řadu křivek a ploch, rozvedl teorii diferenciálních rovnic. Jsou známy Eulerovy integrály, provedl první zpracování variačního počtu, napsal mnoho dalších textů. Podobně jako Euler byl dalším z velkých matematiků Joseph-Louis Lagrange, francouzský matematik a astronom italského původu, který významně rozvinul matematickou analýzu, teorii čísel, klasickou a nebeskou mechaniku. Je znám jako spoluzakladatelem oblasti matematiky, nazývané variační počet.

Na konci 18. století, průmyslová revoluce přinesla velké množství technických problémů. Matematika byla společně s fyzikou připravena k jejich řešení, ale objevovaly se také rozpory. Komplikované funkce, objevující se např. při zkoumání vedení tepla v různých materiálech, si vynutily zpřesnění pojmu funkce, limity, derivace apod.

Augustin Louis Cauchy byl průkopníkem matematické analýzy a rozvíjel dále dílo, které započali Gottfried Wilhelm Leibniz a Sir Isaac Newton. Pracoval také v oblasti komplexní analýzy. K jeho současníkům lze zařadit Bernarda Bolzana, byl jedním z prvních matematiků, kteří v matematické analýze začali uplatňovat rigoróznost. Díla Beyträge zu einer begründeteren Darstellung der Mathematik (1810), Der binomische Lehrsatz (1816) a Rein analytischer Beweis (1817) představovala "...ukázku nového směru vývoje analýzy", která byla až o padesát let později objevena a rozvinuta Karlem Weierstrassem.

Niels Henrik Abel byl norský matematik, který významně ovlivnil funkcionální analýzu. Známý je důkazem nemožnosti obecného řešení rovnic pátého stupně pomocí vzorců

s odmocninami. Po Abelovi se nazývá řada matematických pojmů např.: Abelova grupa, Abelova sumace, Abelovo kritérium. V roce 2002 po něm byla pojmenována Abelova cena. Jeho současník Évariste Galois byl francouzský matematik, formuloval Galoisovu teorii, pomocí které charakterizovat řešení obecného polynomu. Je považován za zakladatele teorie grup.^[9]

Novověk učinil v oblasti geometrie dva důležité kroky: odhalil existenci neeuklidovských geometrií a vytvořil analytickou geometrii.

Descart zavedením kartézské soustavy souřadnic objevuje metodu, jak analyticky, tj. prostřednictvím čísel a rovnic, zkoumat geometrické útvary. Díky tomuto objevu se v následujících staletích podařilo vyřešit mnoho klasických geometrických problémů, např. otázku trisekce úhlu.

Stálé neúspěchy při logickém vyjadřování teorie rovnoběžek si vyžádaly ověřování základů euklidovské geometrie. Negováním pátého Euklidova postulátu o rovnoběžkách se u Lobačevského a Bolyaie objevila neeuklidovská geometrie jako matematicky zcela správná, ze svých axiomů odvoditelná a v okruhu své platnosti bezesporná teorie.

Italský matematik Luca Pacioli zjistil, že rovnici ${\displaystyle x^{4}=a+bx^{2}}$ lze řešit kvadratickou metodou, ale rovnice ${\displaystyle x^{4}+ax^{2}=b}$ nebo ${\displaystyle x^{4}+a=bx^{2}}$ nebyl schopen vyřešit. Scipione del Ferro zastával, stejně jako Pacioli místo na katedře aritmetiky a geometrie Univerzity v Boloni. Del Ferro se zabýval algebraickým řešením kubických rovnic, byl však schopen řešit pouze rovnici tvaru ${\displaystyle x^{3}+mx=n}$.

Až po jeho smrti objevil Niccolò z Brescii, známý pod jménem Tartaglia, obecnou metodu pro řešení všech kubických rovnic. Gerolamo Cardano v Miláně připravoval k vydání svoji práci „Practica Arithmeticae“. Pozval Tartagliu, aby mu prozradil tajemství řešení kubické rovnice. Tartaglia požadoval, aby Cardan zachoval tajemství do doby, než on sám bude řešení publikovat. Cardan ale slib porušil. V roce 1545 publikoval práci „Ars Magna“, první latinské pojednání o algebře. Ta inspirovala řadu matematiků, aby se zabývali řešením kubických a bikvadratických rovnic. Vlastní metody řešení odvodili Viète, Harriot, Euler a Descartes.

K dalšímu vývoji matematické analýzy (infinitezimální počet) od Archimédových začátků došlo až v 16. století, kdy mechanika přivedla matematiky k řešení problémů, jako bylo ohnisko gravitace. Johannes Kepler ve své práci o pohybu planet vypočetl obsah částí elipsy. Svoji metodu založil na představě plochy jako součtu úseček, která v podstatě byla metodou integrace. Fermat také studoval maxima a minima. Zjistil, že funkce dosahuje svého maxima nebo minima, když je tečna křivky této funkce rovnoběžná s osou x. Svoji metodu popsal Descartovi tak, jak ji chápeme dnes: lokální maximum nebo minimum funkce se nachází v bodech, kde je derivace funkce rovna nule.

Skutečnými otci matematické analýzy jsou však Isaac Newton a Gottfried Wilhelm Leibniz. Newton ji vytvořil jako nástroj, který potřeboval pro své fyzikální výpočty. Nazýval ji flexí a její zápis i způsob práce s ní se o dnešního velmi lišil. Není jisté, kolik toho Leibniz o Newtonově metodě věděl (Newton své výsledky obvykle publikoval s velkým zpožděním), ale pár let po Newtonovi také přišel s tímto objevem, ale už s moderním zápisem (např. pro symbol integrálu), matematičtějším pojetím a pojmem „kalkulus“. Ve své době byl spor mezi těmito dvěma objeviteli značně vyhrocený a na mnoho dalších let představoval jablko sváru mezi „kontinentální“ a „ostrovní“ matematikou. Dnešní dějepisci přiznávají zásluhu oběma vědcům.

Termín „integrální počet“ zavedl v roce 1690 Jacob Bernoulli.

Související informace v článku teorie pravděpodobnosti

Teorie pravděpodobnosti a matematická statistika jsou matematické disciplíny spadající do vědního oboru, který se nazývá stochastika. První zmínky nacházíme již v díle Platona Philebos. Obě uvedené disciplíny dosáhly rozmachu až ve 20. století.

Za počátek matematické teorie pravděpodobnosti je považována korespondence Blaise Pascala a Pierre de Fermat v roce 1654. Christian Huygensův spis De ratiociniis in ludo aleae (O uvažování v hazardních hrách) z roku 1657 byl první tištěnou prací v této oblasti. Poté byl přetištěn v první části knihy Ars conjectandi (Nauka o domněnce) Jacoba Bernoulliho, který doplnil či zobecnil Huygensovy myšlenky a začala vznikat teorie pravděpodobnosti v dnešním pojetí této matematické disciplíny.

V 18. století se teorií pravděpodobnosti zabýval rod Bernoulliů. Jejich hlavním vkladem je spis Jakoba Bernoulliho Ars coniectandi, napsaný mezi lety 1679–1685 a vydaný Jakobovým synovcem Niclausem v r. 1713. V r. 1774 publikoval první práci věnovanou teorii pravděpodobnosti Pierre Simon Laplace v knize Théorie analytique des probabilités (nebo Essai philosophique sur les probabilités). Laplace shrnul a prohloubil vše, čeho bylo v této oblasti do té doby dosaženo.^[10]

Za hlavní rysy dalšího vývoje teorie pravděpodobnosti lze považovat pronikání metod diferenciálního a integrálního počtu (včetně teorie řad) a s tím související studium spojitých náhodných veličin; také uplatňování teorie pravděpodobnosti při zpracování výsledků astronomických a geodetických pozorování (představitelé: Abraham de Moivre a věta Moivreova – Laplaceova nebo Carl Friedrich Gausse). V průběhu 19. století se neobjevují zásadní nové podněty v této oblasti.

Vyšetřování řady konkrétních číselných systémů (kvaterniony, oktávy, triplety, matice atd.) podmiňovalo v 2.polovině 19. století postupný vývoj teorie hyperkomplexních čísel (Benjamin Peirce (1809–1880) vytvořil pojem lineární asociativní algebra). Matematici pracovali s lineárními kombinacemi, lineárními závislostmi, lineárními nezávislostí, s generováním, bázemi a souřadnicemi, lineárními transformacemi, zavedli pojem dimenze. V teorii hyperkomplexních čísel se utvářely důležité pojmy moderní algebry – těleso, vektorový prostor, maticová reprezentace atd. Objev vztahů mezi teorií asociativních algeber a teorií reprezentací grup (v osmdesátých letech 19. století) měl zásadní význam pro další rozvoj algebry.

Americký matematik Leonard Eugene Dickson (1874–1954) působil na univerzitě v Chicagu, patří mezi největší znalce teorie čísel (třídílná monografie History of the theory of numbers). Roku 1903 v práci Definitions of a linear associative algebra by independent postulates zpřesnil definici pojmu lineární asociativní algebra. Obecnou teorií algeber nad libovolným tělesem se jako první zabýval Joseph H. M. Wedderburn (1882–1948).^[11]

V matematice se tak začaly z vnitřních problémů její výstavby tvořit teorie, které byly logicky správné a při tom často neodpovídaly žádné známé situaci z reálného světa. Začala nová etapa vývoje matematiky, kdy se předmětem zkoumání staly abstraktní kvantitativní vztahy a geometrické objekty.

Teorie her jako samostatná vědní disciplína je velmi mladá, o skutečné prehistorii teorie her lze o hovořit v souvislosti se vznikem počtu pravděpodobnosti (ve spojení se jmény Pascal, Fermat, Bernoulli). Emile Borel publikoval v letech 1921 až 1927 v oblasti teorie pravděpodobnosti sérii francouzsky psaných poznámek, jako první se pokusil o matematizaci pojmu strategická hra. Kdo by měl být považován za zakladatele matematické teorie her, to byl zásadní předmět sporu: Emile Borel, který na jedné straně jako první studoval pojem strategická hra v obecnějším smyslu, nebo John von Neumann, jehož první práce byla publikována o několik let později, stala se ale skutečným stimulem pro další vývoj teorie. John von Neumann položil základy teorie her jako samostatné matematické disciplíny a zasloužil se o rozšíření jejích aplikací do dalších oborů. Významným mezníkem ve vývoji teorie her bylo dílo Theory of Games and Economic Behavior z roku 1944, jež byla výsledkem spolupráce Johna von Neumanna s ekonomem Oskarem Morgensternem.

John Forbes Nash studoval kooperativní hry a jejich redukci používal na hry nekooperativní; v této souvislosti se hovoří o Nashově programu. V roce 1994 získal John F. Nash spolu s Johnem C. Harsanyim a Reinhardem Seltenem Nobelovu cenu za ekonomii za průkopnickou analýzu rovnováhy v teorii nekooperativních her.^[12]

V dvacátých letech 20. století formuloval slavný německý matematik David Hilbert tzv. Hilbertův program. Ten měl za cíl vystavět matematiku na neotřesitelných logických základech, především na bezrozporné teorii množin. Na přelomu století se totiž nejlepší matematikové zabývali problém, jak se vyhnout paradoxům, které s sebou tehdejší příliš volné množinové definice, dnes už víme že nevyhnutelně, přinášely. Hilbert věřil, že matematiku na takovýchto bezrozporných základech postavit lze. Je autorem slavného výroku: „Musíme vědět. Budeme vědět.“

Hned v roce 1931 však přišel mladý Rakušan Kurt Gödel a jedním chytrým důkazem celou snahu položil na kolena. Ukázal, že každý axiomatický systém obsahující aritmetiku je nutně neúplný – tedy že v něm existují pravdivá tvrzení, která však nelze prostředky systému dokázat. Tento výsledek se zařadil po bok podobných deziluzivních objevů tehdejší doby, jako byla Schrödingerova neurčitost a značně zmírnil modernistickou víru v možnosti vědy a techniky.

Do tohoto leptání matematického sebevědomí se krátce poté zapojil britský matematik Alan Turing, když negativně rozřešil tzv. „Entscheidungsproblem“. Při této příležitosti vytvořil model Turingova stroje, čímž položil teoretické základy teorii složitosti a vůbec celé informatiky, nového odvětví matematiky zabývající se zejména algoritmizací.

Počítače se ukázaly být poměrně revoluční změnou v chápání užitečnosti matematiky. Na jednu stranu se jejich konstrukce neobejde bez chytrých matematických aplikací (viz např. šifrovací algoritmus RSA), na druhou stranu umožňují mechanicky procházet mnohem víc možností, než by stihli lidé a tak podlamují praktickou užitečnost matematického důkazu. I ten navíc pod jejich vlivem doznává změn: V roce 1976 byla dokázána věta o čtyřech barvách počítačovou analýzou tisíce případů, na které šlo hlavní problém rozložit a dlouho se vedly spory, je-li takovýto způsob vedení důkazu korektní.

Ve dvacátém století se vyskytlo několik pozoruhodných případů nestandardního zacházení se základním matematickým nástrojem, důkazem. Vedle již zmíněného důkazu věty o čtyřech barvách, které počítač asistoval, vyskytly se pokusy o plně automatické dokazování vět. Počítač v nich dostane sadu axiomů zadaných symboly výrokové logiky a z nich vyvozuje stále složitější vlastnosti systému.

Kvalita tohoto odvozování a dokazování je zatím samozřejmě nedostatečná. Ostatně intuice živých matematiků může slavit ohromné úspěchy i bez znalosti pojmu „důkaz“: indický matematik Rámanudžan ve dvacátých letech odvodil mnoho hlubokých pravd čistě na základě matematického vhledu.

V této době se matematikou zabývá nebývalé množství lidí. Roste počet matematických časopisů, jejich záběr je hlubší i širší. Vznikají nové obory, ty stávající se štěpí.

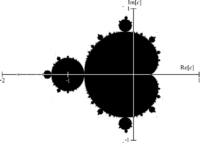
Jako příklad matematických novinek z tohoto období můžeme uvést fraktály. Jde o novou oblast zkoumání geometrie, která se zabývá soběpodobnými útvary, tj. útvary, jejichž část vykazuje podobnost s celkem. Ačkoliv jsou definice známých fraktálů jednoduché, jejich tvar i chování vykazuje podivuhodnou složitost (viz článek RSA).

Výrazného rozkvětu se dočkala teorie grafů. Na stavbu jejích základů zavdal již Euler, když v roce 1736 vyřešil problém mostů v Královci. Jako samostatná disciplína se však tato odnož kombinatoriky etablovala až v polovině dvacátého století, kdy byly vydána první kniha věnovaná teorii grafů.

Aplikačně jde o nesmírně důležitý obor. Pomáhá v návrzích optimálních komunikačních a transportních sítí, zvyšuje rychlost počítačových algoritmů atd.

Do jejich dějin se výrazně zapsalo i několik českých matematiků: Vojtěch Jarník a Otakar Borůvka, kteří ve třicátých letech vyřešili problém konstrukce minimální kostry grafu.^[13]

V souvislosti s touto expanzí roste význam hledání mostů mezi jednotlivými podobory. Naprosto odlišně vypadají matematické struktury mohou mít silné společné vlastnosti, za pomoci kterých mohou jít vyřešit složité otázky v jedné struktuře převedením do druhé, ve které tak složité nebudou.

Pomocí právě popsané metody byla v roce 1994 vyřešena velká Fermatova věta. Angličan Andrew Wiles dokázal dostatečně velkou část Tanijamovy–Šimurovy věty, čímž vytvořil nový most mezi algebrou a geometrií a automaticky tak dokázal staletí vzdorující Fermatův problém.^[14]

Sto let starou Poincarého domněnku proměnil v roce 2006 ve větu ruský matematik Grigorij Perelman. Poincarého domněnka je první a zatím jediný vyřešený problém milénia.

Mezi významné osobnosti matematiky, které působily na našem území v 17. století lze zařadit Vavřince Benedikta z Nudožer. V 18. století se začala matematika rozvíjet i v Evropě; vedle Stanislava Vydry patří k velmi významným osobnostem Bernard Bolzano, který jako první poskytl čistě analytický důkaz základní věty algebry a Bolzanovy věty.

Ve 20. století se Češi stali rovnocennými partnery evropských matematiků. Eduard Čech se zasloužil o rozvoj topologie a diferenciální geometrie. Václav Hlavatý vyřešil některé velmi obtížné rovnice vztahujících se k Einsteinově jednotné teorii pole. Jaroslav Hájek patřil mezi nejvýznamnější světové teoretické statistiky. Jindřich Nečas byl významný český matematik působící v oboru parciálních diferenciálních rovnic, nelineární funkcionální analýzy a jejich aplikacích v mechanice tekutin. Ivo Babuška se proslavil aplikovanou numerickou matematikou. Otakar Borůvka pracoval v teorii grafů, sestrojil tzv. Borůvkův algoritmus. Jaroslav Kurzweil objevil obecnou definici integrálu. Vojtěch Jarník se věnoval teorii čísel a matematické analýze, sestrojil tzv. Jarníkův algoritmus.^[15]

Miroslav Katětov, který se zabýval především topologií a funkcionální analýzou, sestrojil tzv. Katětov-Tongovu větu; byl i výborný šachista. Petr Vopěnka je známý zejména vytvořením alternativní teorii množin. Jaroslav Nešetřil patří mezi významné matematiky zabývající se diskrétní matematikou. Petr Hájek je světově uznávaný vědec v oblasti matematické logiky, Václav Chvátal pracoval v teorii grafů, sestrojil mimo jiné tzv. Chvátalův graf.^[15]

David Preiss jako profesor matematiky na University of Warwick obdržel v roce 2008 os London Mathematical Society cenu Pólya Prize za práci o geometrii měr.^[16] Vladimír Šverák z Minnesotské univerzity je znám jako významný odborník na parciální diferenciální rovnice. Tento výčet není rozhodně úplný, mnoho osobností by bylo možno ještě připomenout.

Na matematiky stále čeká mnoho klasických nevyřešených problémů. S každým novým výsledkem navíc vystupují další otázky. Není třeba se bát o nedostatek práce – budoucí matematika se ale bude muset filosoficky vyrovnat s rychlými počítači a také bude muset vylepšit práci s existujícími znalostmi, kterých bude čím dál tím více.

V roce 2009 zahájil Timothy Gowers projekt Polymath, v rámci kterého se množství dobrovolníků z celého světa podílelo na společném hledání alternativního důkazu hustotní Hales-Jewettovy věty ryze webovými prostředky, tedy prostřednictvím blogů, komentářů a wiki. Po šesti týdnech práce byl důkaz pravděpodobně nalezen.^[17]

V tomto článku byl použit překlad textu z článku Dějiny matematiky na norské (bokmål) Wikipedii.

• MANDELBROT, Benoît. Fraktály. Praha: Mladá Fronta, 2003. ISBN 80-204-1009-0. 
• ŠIŠMA, Pavel. Teorie grafů 1736-1963. Brno: Prometheus, 1997. ISBN 80-7196-065-9. 
• VOPĚNKA, Petr. Rozpravy s geometrií. Praha: Panorama, 1989. 
• VOPĚNKA, Petr. Vyprávění o kráse novobarokní matematiky. Praha: Práh, 2004. ISBN 80-7252-103-9. 
• Matematika v proměnách věků III. Příprava vydání Jindřich Bečvář, Eduard Fuchs. Praha: Výzkumné centrum pro dějiny vědy, 2004. ISBN 80-7285-040-7. 
• BEČVÁŘ J.: Z historie lineární algebry, Katedra didaktiky matematiky, Matematicko-fyzikální fakulta Univerzity Karlovy, Matfyzpress, Praha, 2007, 519 stran, ISBN 978-80-7378-036-4.
• BEČVÁŘ J., FUCHS E. (ed.): Historie matematiky I, Sborník, Seminář pro vyučující na středních školách, Jevíčko, srpen 1993, JČMF, Brno 1994, 241 stran.
• BEČVÁŘ J., FUCHS E. (ed.): Historie matematiky II, Sborník, Seminář pro vyučující na středních školách, Jevíčko, 21. 8. – 24. 8. 1995, Prometheus, Praha 1997, 194 stran, ISBN 80-7196-046-2.
• BEČVÁŘ J., FUCHS E. (ed.): Matematika v proměnách věků I, Sborník, Prometheus, Praha 1998, 218 stran, ISBN 80-7196-107-8.
• BEČVÁŘ J., FUCHS E. (ed.): Matematika v proměnách věků II, Prometheus, Praha 2001, 267 stran, ISBN 80-7196-218-X.
• BEČVÁŘ J., FUCHS E. (ed.): Matematika v proměnách věků III, Výzkumné centrum pro dějiny vědy, Praha 2004, 253 stran, ISBN 80-7285-040-7.
• FUCHS E. (ed.): Matematika v proměnách věků IV, Akademické nakladatelství CERM, Brno, 2007, 223 stran, ISBN 978-80-7204-536-5.
• BEČVÁŘOVÁ M., BEČVÁŘ J. (ed.): Matematika v proměnách věků V, Matfyzpress, Praha, 2007, 331 stran, ISBN 978-80-7378-017-3.
• BEČVÁŘ J., BEČVÁŘOVÁ M. (ed.): Matematika v proměnách věků VI, Matfyzpress, Praha, 2010, 231 stran, ISBN 978-80-7378-146-0.
• BEČVÁŘ J., FUCHS E. (ed.): Matematika v 16. a 17. století, Sborník, Seminář Historie matematiky III., Jevíčko, 18.8. – 21. 8. 1997, Prometheus, Praha 1999, 321 stran, ISBN 80-7196-150-7.
• BEČVÁŘOVÁ M.: Eukleidovy Základy, jejich vydání a překlady, Prometheus, Praha 2002, 297 stran, ISBN 80-7196-233-3.
• BEČVÁŘ J. a kol.: Matematika ve středověké Evropě, Prometheus, Praha 2001, 445 stran, ISBN 80-7196-232-5.
• HUDEČEK J.: Matematika v devíti kapitolách. Překlad, vysvětlivky a úvod, Katedra didaktiky matematiky, Matematicko-fyzikální fakulta Univerzity Karlovy, Matfyzpress, Praha, 2008, 244 stran, ISBN 978-80-7378-046-3.
• MAREŠ, Milan. Příběhy matematiky. 2. vyd. Praha: Pistorius & Olšanská, 2011. ISBN 978-80-87053-64-5. 
• MAČÁK K.: Počátky počtu pravděpodobnosti, Prometheus, Praha 1997, 111 stran, ISBN 80-7196-089-6.
• SCHWABIK Š., ŠARMANOVÁ P.: Malý průvodce historií integrálu, Prometheus, Praha 1996, 95 stran, ISBN 80-7196-038-1.
• ŠOLCOVÁ, A.: Kapitoly z historie matematiky a informatiky, Česká technika – nakladatelství ČVUT v Praze, 2017, ISBN 978-80-01-06092-6.
• Řecké matematické texty. Příprava vydání Z. Šír (výběr textů, úvodní studie a poznámky), R. Mašek a A. Šmíd (překlad). Praha: Oikúmené, 2011. ISBN 978-80-7298-308-7. 

• BOURBAKI, Nicolas. Elements of the History of Mathematics. [s.l.]: Springer-Verlag, 1998. Dostupné online. ISBN 3-540-64767-8. 

• Obrázky, zvuky či videa k tématu dějiny matematiky na Wikimedia Commons
• Vývoj matematiky a fyziky od počátku k dnešku
• První české stránky věnované historii matematiky