Didymické ladění
Didymické ladění je nejběžnější z čistých hudebních ladění. Mnohdy bývá pojmem čisté ladění označováno právě ladění didymické.
Toto ladění zní absolutně čistě v tónině odvozené od základního tónu, již ve velmi příbuzných tóninách se ale začínají vyskytovat velice disonantní vlčí intervaly, takže čisté ladění je pro složitější hudbu prakticky nepoužitelné. Příkladem může být vlčí kvinta d-a: (5:3) x (8:9) = 40:27, čili asi 1,4815; čistá kvinta je 3:2 = 1,5.
Základ ladění vytvořil v prvním století hudební teoretik Didymus z Alexandrie, který vyšel z dělení struny v poměru 24:27:30:32. Jeho tetrachord má následující strukturu (jak je u starých řeckých stupnic obvyklé, jsou tóny uváděny v sestupném pořadí):
| mese | lichanos | parhypate | hypate | |||
|---|---|---|---|---|---|---|
| 1:1 | 8:9 | 4:5 | 3:4 | |||
| 0 | 203,91 centů | 386,31 centů | 498,04 centů | |||
| 8:9 | 9:10 | 15:16 | ||||
| 203,91 centů | 182,40 centů | 111,73 centů |
K oktávě 2:1 a kvintě 3:2, které byly použity již při konstrukci pythagorejského ladění, byly přidány intervaly, v nichž se objevuje číslo 5. Disonantní Pythagorejská velká tercie 81:64 byla nahrazena Didymickou velkou tercií 5:4 a Pythagorejská velká sexta 27:16 Didymickou sextou 5:3. Rozdíl mezi Pythagorejskou a Didymickou tercií nebo Pythagorejskou a Didymickou sextou se nazývá Didymické koma.
Sedmitónová stupnice
Pro odvození tónů používá didymické ladění jen kvintu, velkou tercii a oktávu.
Tóny d, f a g se odvodí postupnými kvintovými kroky stejným způsobem jako u Pythagorejského ladění: tón f jako kvinta pod základním tónem c, transpozice o oktávu výše: (1:1) x (2:3) x (2:1) = (4:3); g o kvintu výše než c: (1:1) x (3:2) = (3:2); d o kvintu výše než g, transpozice o oktávu níž: (3:2) x (3:2) x (1:2) = (9:8). Tóny e, a a h se odvodí z velkých tercií: e o velkou tercii výše než c: (1:1) x (5:4) = (5:4); a o velkou tercii výše než f: (4:3) x (5:4) = (5:3); h o velkou tercii výše než g: (3:2) x (5:4) = (15:8).
Tímto postupem vznikne sedmitónová stupnice složená ze samých čistých intervalů: velká sekunda (9:8), velká tercie (5:4), kvarta (4:3), kvinta (3:2), velká sexta (5:3), velká septima (15:8) a oktáva (2:1). Jednotlivé tóny této stupnice jsou vzdáleny o velký celý tón (9:8), malý celý tón (10:9) nebo diatonický půltón (16:15).
| c | d | e | f | g | a | h | c | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1:1 | 9:8 | 5:4 | 4:3 | 3:2 | 5:3 | 15:8 | 2:1 | |||||||
| velký celý tón | malý celý tón | půltón | velký celý tón | malý celý tón | velký celý tón | půltón | ||||||||
| 9 : 8 | 10 : 9 | 16 : 15 | 9 : 8 | 10 : 9 | 9 : 8 | 16 : 15 | ||||||||
| 204 centů | 182 centů | 112 centů | 204 centů | 182 centů | 204 centů | 112 centů |
Dvanáctitónová stupnice
Jen pomocí kvint a velkých tercií lze dále vytvořit i dvanáctitónovou chromatickou stupnici složenou ze samých čistých intervalů.
| Tón | Poměr frekvencí k předchozímu tónu | Poměr frekvencí k základnímu tónu | Kvocient | Centy | Vztah ke kvintovému kruhu |
|---|---|---|---|---|---|
| c | 16 : 15 | 1 : 1 | 1 | 0,000 | |
| des | 16 : 15 | 16 : 15 | 1,0666… | 111,731 | velká tercie pod f |
| d | 135 : 128 | 9 : 8 | 1,125 | 203,910 | |
| es | 16 : 15 | 6 : 5 | 1,2 | 315,641 | velká tercie pod g |
| e | 25 : 24 | 5 : 4 | 1,25 | 386,314 | velká tercie nad c |
| f | 16 : 15 | 4 : 3 | 1,333… | 498,045 | |
| fis | 135 : 128 | 45 : 32 | 1,40625 | 590,224 | velká tercie nad d |
| g | 16 : 15 | 3 : 2 | 1,5 | 701,955 | |
| as | 16 : 15 | 8 : 5 | 1,6 | 813,686 | velká tercie pod c |
| a | 25 : 24 | 5 : 3 | 1,666… | 884,359 | velká tercie nad f |
| b | 16 : 15 | 16 : 9 | 1,777… | 996,090 | |
| h | 135 : 128 | 15 : 8 | 1,875 | 1088,269 | velká tercie nad g |
| c | 16 : 15 | 2 : 1 | 2 | 1200,000 |
Rozdíly mezi jednotlivými tóny mají následující velikosti a názvy:
| Název | Podíl frekvencí | Centy | Příklad |
|---|---|---|---|
| Diatonický půltón | 16 : 15 | 111,731 | e-f |
| Velký chromatický půltón | 135 : 128 | 92,179 | f-fis |
| Malý chromatický půltón | 25 : 24 | 70,672 | es-e |
Takto sestavená chromatická stupnice nemá ale prakticky žádné využití, již bylo řečeno, že při modulacích i do blízkých tónin se objevují velké disonance nepříjemné pro poslech.
Externí odkazy
 Obrázky, zvuky či videa k tématu Didymické ladění na Wikimedia Commons
Obrázky, zvuky či videa k tématu Didymické ladění na Wikimedia Commons
Média použitá na této stránce
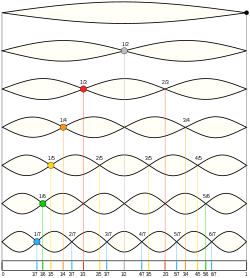
Just intonation based on dominant positions
