Diffieho–Hellmanův protokol s využitím eliptických křivek

Animovaný princip ECDH

Diffieho-Hellmanův protokol s využitím eliptických křivek (ECDH) je varianta Diffieho-Hellmanova protokolu, který využívá eliptických křivek. Jde o šifrovací protokol, který umožňuje dvěma stranám, které se v životě nesetkaly ani spolu nekomunikovaly, sdílet „tajné“ informace na nechráněném komunikačním kanálu (to jest na sdělovacím kanálu, přes který se posílají informace, například telefon). Tyto informace mohou být přímo použity jako klíč, nebo ještě lépe, na vytvoření jiného klíče, který může být použit k zašifrování další komunikace s použitím symetrické šifry.

Vytváření klíče

Předpokládejme, že první účastník - Alice - chce vytvořit sdílený klíč s druhým účastníkem - Bobem, ale na jediném místě, kde spolu mohou komunikovat, se nachází špehové. Předně se musí dohodnout na parametrech (p, a, b, G, n, h), kde p je prvočíslo, kterým definujeme těleso, konstanty a, b z rovnice eliptické křivky, bod G na eliptické křivce, jeho řád n a kofaktor h, který udává podíl počtu prvků grupy bodů na eliptické křivce a řádu bodu G.

Nyní si každá strana musí zvolit své klíče, které se skládají ze soukromého klíče d (náhodně vybrané celé kladné číslo z intervalu [1,n-1]) a veřejného klíče Q, kde ${\displaystyle Q=dG}$. Alice tedy bude mít dvojici ${\displaystyle d_{A},Q_{A}}$ Bob bude mít ${\displaystyle d_{B},Q_{B}}$. Aby tento protokol fungoval, strany si musí vyměnit veřejné klíče (Alice pošle Bobovi ${\displaystyle Q_{A}}$, Bob pošle Alici ${\displaystyle Q_{B}}$).

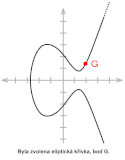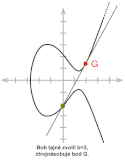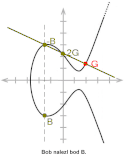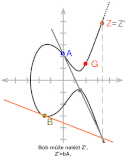
Nyní může Alice nalézt bod Z, ${\displaystyle Z=d_{A}Q_{B}}$, Bob může nalézt bod Z', ${\displaystyle Z'=d_{B}Q_{A}}$. Tyto body Z, Z' jsou totožné, neboť ${\displaystyle Z=d_{A}Q_{B}=d_{A}(d_{B}G)=d_{A}d_{B}G=d_{B}(d_{A}G)=d_{B}Q_{A}=Z'}$.

Příklad

• Alice a Bob zvolí prvočíslo ${\displaystyle p=23}$, bod G[13;16], koeficienty ${\displaystyle a=1,b=1}$.
  • ${\displaystyle 4a^{3}+27b^{2}\neq 0\mod 23}$, jde tedy o eliptickou křivku.
• Alice zvolí ${\displaystyle d_{A}=2}$, spočítá ${\displaystyle Q_{A}=2G}$:
  • ${\displaystyle s\equiv {\frac {3x^{2}+a}{2y}}\mod p\equiv {\frac {3\cdot 13^{2}+1}{2\cdot 16}}\mod 23\equiv 13\mod 23}$
  • ${\displaystyle x_{A}\equiv s^{2}-2x\mod p\equiv 13^{2}-2\cdot 13\mod 23\equiv 5\mod 23}$
  • ${\displaystyle y_{A}\equiv s(x-x_{A})-y\mod p\equiv 13(13-5)-16\mod 23\equiv 19\mod 23}$
  • Alice získává souřadnice bodu ${\displaystyle Q_{A}[5;19]}$, tento bod posílá Bobovi.
• Bob zvolí ${\displaystyle d_{B}=4}$, spočítá ${\displaystyle Q_{B}=2\cdot 2G=2R}$:
  • Bob analogicky zdvojnásobí bod G, získá pomocný bod R, který opět zdvojnásobí.
  • Bob získává souřadnice bodu ${\displaystyle Q_{B}[17;3]}$, tento bod posílá Alici.
• Alice nyní může nalézt bod Z:
  • ${\displaystyle Z\equiv d_{A}Q_{B}\mod 23\equiv 2\cdot [17;3]\mod 23=[13;16]}$
• Bob může nalézt bod Z':
  • ${\displaystyle Z'\equiv d_{B}Q_{A}\mod 23\equiv 4\cdot [5;19]\mod 23=[13;16]}$
• Z=Z'

Pozn.: Byly zvoleny nevhodné koeficienty, stejně jako ostatní čísla, příklad je pouze ilustrační.

Bezpečnost

Tento protokol je bezpečný, neboť se nezveřejnilo nic kromě veřejných klíčů, které nejsou tajné, a ani jedna strana nedokáže zjistit soukromý klíč té druhé, pokud by nevyřešila problém diskrétního logaritmu u eliptických křivek.

Veřejné klíče jsou buď neměnné (a shledané důvěryhodnými třeba pomocí certifikátů), nebo dočasné. Dočasné klíče nejsou nutně ověřené, takže pokud je ověření vyžadováno, je třeba jej zajistit jinými způsoby.

Diffieho-Hellmanova výměna klíčů je ale napadnutelná (může obsahovat zadní vrátka).^[1]

Reference