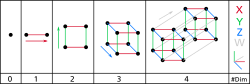Dimenze
Dimenze nebo rozměr nějakého objektu je v matematice a fyzice neformálně řečeno nejmenší počet souřadnic, které musíme znát, abychom jednoznačně určili bod tohoto objektu. Například křivka (čára) je jednorozměrná (jednodimenzionální, má dimenzi jedna), protože k určení bodu stačí např. vzdálenost tohoto bodu od nějakého vyznačeného bodu na křivce. Koule je třírozměrná a její povrch dvourozměrný. Prostor, ve kterém žijeme, je z hlediska fyziky čtyřrozměrný: má tři prostorové dimenze (výška, hloubka, šířka) a jednu časovou dimenzi (tzv. časoprostor).
| počet dimenzí | příklady |
|---|---|
| nula dimenzí | bod |
| jedna dimenze | úsečka, křivka, přímka, kružnice |
| dvě dimenze | plocha (kruh, čtverec, povrch toru…) |
| tři dimenze | tělesa (krychle, kvádr…) |
| čtyři dimenze | čtyřrozměrná tělesa (hyperkrychle…), časoprostor |
Dimenze vektorového prostoru se rovná počtu vektorů jeho báze. Prostory se nemusejí vázat na konkrétní fyzikální objekty a mohou být i nekonečnorozměrné; takové jsou například prostory nekonečných posloupností čísel. Pro složité množiny (typicky fraktály) existují definice dimenze, jež nemusejí být celočíselné. Často se k tomuto účelu používá Hausdorffova (fraktální) dimenze. Pojem dimenze se přenáší i na algebraické struktury, jež nemají nutně prostorový charakter, například Krullova dimenze se týká komutativních okruhů.
Literatura
- PAUŠ, Petr. Počítačová analýza fraktálních množin [online]. Praha: FJFI ČVUT, 2005 [cit. 2019-07-04]. Dostupné online.
Externí odkazy
Obrázky, zvuky či videa k tématu dimenze na Wikimedia Commons
Média použitá na této stránce
Autor: NerdBoy1392, Licence: CC BY-SA 3.0
A drawing of the first four dimensions. On the left is zero dimensions (a point) and on the right is four dimensions (A tesseract). There is an axis and labels on the right and which level of dimensions it is on the bottom. The arrows alongside the shapes indicate the direction of extrusion.