Dioklova kisoida

Dioklova kisoida (zastarale cissoida, cisoida^[1]) je druh rovinné kubické křivky s jedním hrotem. Někdy se jí říká krátce kisoida, jindy se kisoidou myslí obecnější druh křivek, jejichž je Dioklova kisoida speciálním případem.^[2]

Konstrukce

Kružnicí a přímkou

Na dané kružnici ${\displaystyle K}$ se vyznačí dva protilehlé body, ${\displaystyle O}$ a ${\displaystyle A}$, a bodem ${\displaystyle A}$ se vede tečna ${\displaystyle t}$ ke kružnici ${\displaystyle K}$. Pro každou z přímek ze svazku přímek se středem ${\displaystyle O}$ (tedy pro všechny sečny procházející ${\displaystyle O}$) se určí vždy jejich druhý průsečík ${\displaystyle M_{1}}$ s kružnicí a průsečík ${\displaystyle M_{2}}$ s tečnou ${\displaystyle t}$. Kisoidě pak přísluší ten bod ${\displaystyle M}$ na úsečce ${\displaystyle OM_{2}}$, pro který je ${\displaystyle |OM|=|M_{1}M_{2}|}$.

Tato konstrukce odpovídá konstrukci obecné kisoidy, kde je jako jedna z vytvořujících křivek použita kružnice ${\displaystyle K}$ a jako druhá přímka ${\displaystyle t}$. V bodě ${\displaystyle O}$ se pak nachází hrot a přímka ${\displaystyle t}$ je asymptotou zkonstruované Dioklovy kisoidy.

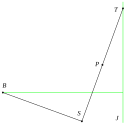
Newtonova pravým úhlem

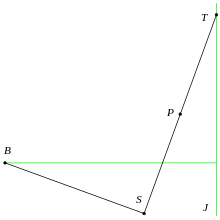
Na začátku je dána pevná přímka ${\displaystyle J}$ a bod ${\displaystyle B}$. Dioklově kisoidě pak náleží takové body ${\displaystyle P}$, které leží ve středu úseček ${\displaystyle ST}$ takových, že úhel ${\displaystyle BST}$ je pravý a ${\displaystyle T}$ náleží ${\displaystyle J}$.

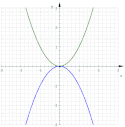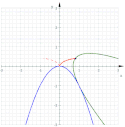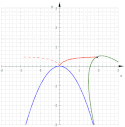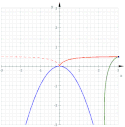
Parabolami

Jsou-li dvě paraboly o společném vrcholu a protisměrných osách, pak při kotálení jedné paraboly po druhé opisuje její vrchol Dioklovu kisoidu.

Dějiny

Dioklovu kisoidu poprvé zkoumal starořecký matematik Dioklés v 2. století před naším letopočtem (patřičnou část jeho nedochované práce O zápalných zrcadlech cituje Eutokios ve svém komentáři Archimédova pojednání O kouli a válci^[3]), proto se nazývá Dioklova. Slovo kisoida je rovněž starořeckého původu a vychází ze slova κισσός znamenajícího břečťan.^[3] Dříve používaná varianta cisoida vychází z latinské varianty zápisu.^[1]

V 17. století byla jednou z křivek, na kterých zkoušeli průkopníci infinitesimálního počtu své postupy na výpočet obsahu a konstrukci tečny.^[2]

Významně se Dioklově kisoidě a i kisoidám obecným (které nazýval cissoidály) věnoval ve své kariéře český matematik Karel Zahradník.^[4]

Vyjádření Dioklovy kisoidy

• implicitně v kartézské soustavě souřadnic: ${\displaystyle y^{2}(2a-x)-x^{3}=0}$^[5]
• parametrické vyjádření: ${\displaystyle x={\frac {at^{2}}{1+t^{2}}},y={\frac {at^{3}}{1+t^{2}}}}$^[2]

Odkazy

Reference

Externí odkazy

• Obrázky, zvuky či videa k tématu Dioklova kisoida na Wikimedia Commons
• Encyklopedické heslo Cissoida v Ottově slovníku naučném ve Wikizdrojích