Doplněk množiny

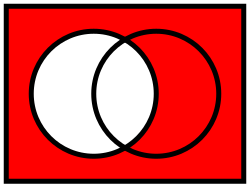
V matematice se pojmy doplněk množiny ${\displaystyle A}$ nebo komplement množiny ${\displaystyle A}$ označuje množina ${\displaystyle A^{C}}$ všech prvků, které nejsou v ${\displaystyle A}$ a přitom v nějaké jiné (předem dané) množině jsou obsaženy (na obrázku v ${\displaystyle U}$). Aby bylo možné doplněk definovat, je třeba znát množinu, vzhledem ke které se doplněk počítá. Je to operace ekvivalentní množinovému rozdílu ${\displaystyle U-A}$.

Místo ${\displaystyle A^{c}}$ se někdy užívá značení ${\displaystyle A'}$ nebo ${\displaystyle -A}$

Formální definice

Máme-li množinu ${\displaystyle U}$ a její podmnožinu ${\displaystyle A}$, definujeme doplněk množiny ${\displaystyle A}$ vzhledem k množině ${\displaystyle U}$ jako ${\displaystyle A^{C}=\{x\mid x\in U\wedge x\not \in A\}}$. Tedy ${\displaystyle A^{C}}$ obsahuje všechny prvky, které jsou v ${\displaystyle U}$, ale nejsou v ${\displaystyle A}$.

Pokud máme pevně danou univerzální množinu ${\displaystyle U}$, můžeme zkráceně hovořit jen o „doplňku ${\displaystyle A}$“.

Příklady

Pokud ${\displaystyle U=\{a,b,c\}}$ je univerzální množina a ${\displaystyle A=\{b\}}$, je ${\displaystyle A^{C}=\{a,c\}}$

Pokud za univerzální množinu vezmeme množinu všech přirozených čísel bez nuly, doplňkem všech lichých čísel je množina všech sudých čísel. Doplňkem množiny ${\displaystyle \{1,2\}}$ je pak množina všech přirozených čísel větších než 2.

Pokud jsou univerzální množinou reálná čísla, je doplňkem všech algebraických čísel množina všech transcendentních čísel.

Vlastnosti

Následující pravidla uvádí několik základních vlastností doplňku množiny. Mějme univerzální množinu ${\displaystyle U}$ a její podmnožiny ${\displaystyle A}$, ${\displaystyle B}$

• A ∪ A^C  =  U
• A ∩ A^C  =  ∅
• ∅^C  =  U
• U^C  =  ∅
• Pokud A⊆B, pak B^C⊆A^C
• A^CC  =  A.

De Morganovy zákony:

• (A ∪ B)^C = A^C ∩ B^C
• (A ∩ B)^C = A^C ∪ B^C

Související články

• Množinové operace
• Průnik
• Sjednocení
• Rozdíl množin
• UNION