Dračí křivka

10. iterace dračí křivky

Dračí křivka (z angl. Dragon curve) je soběpodobná křivka, která má vlastnosti fraktálu. Může být aproximována např. L-systémem nebo systémem iterovaných funkcí. Poprvé jí popsal fyzik z výzkumného střediska NASA John Heighway,^[1] po kterém je někdy nazývána „Heighway Dragon“.

Vlastnosti

• soběpodobnost – dračí křivka má mnoho sobě-podobných částí, které jsou vzájemně otočeny o 45° a jejich velikosti jsou násobky v poměru 1:√2

• rozměry křivky jsou 1,5 × 1 (při délce výchozí úsečky 1)

• délka křivky se každou iterací násobí √2, z každého segmentu délky s se stanou dva segmenty délky ${\displaystyle \textstyle {s \over {\sqrt {2}}}}$

${\displaystyle {2s \over {\sqrt {2}}}={2s \over {\sqrt {2}}}\cdot {{\sqrt {2}} \over {\sqrt {2}}}={\sqrt {2}}s}$

• křivka nikdy neprotne sama sebe, to je vidět, když se vykreslí se zkosenými rohy

• fraktálová dimenze křivky je ${\displaystyle \textstyle {{\ln 2 \over \ln {\sqrt {2}}}=2}}$, jedná se tedy o plochu-vyplňující křivku
• plocha křivky je ${\displaystyle \textstyle {1 \over 2}}$ (při délce výchozí úsečky 1)
• fraktálovou dimenzi hranice křivky numericky aproximovali Angel Chang a Tianrong Zhang,^[2] dnes již známe analytické vyjádření:^[3]

${\displaystyle \log _{2}\left({\frac {1+{\sqrt[{3}]{73-6{\sqrt {87}}}}+{\sqrt[{3}]{73+6{\sqrt {87}}}}}{3}}\right)\cong 1.523627086202492.}$

Konstrukce

Jedna z možných konstrukcí je následující. Začne se s úsečkou o libovolné délce. V Každém kroku se nad každou úsečkou postaví pravoúhlý rovnoramenný trojúhelník. Přepona tohoto trojúhelníka bude výchozí úsečka a orientace trojúhelníka se bude střídat, na první úsečce doleva, na druhé doprava (směr vzhledem k průchodu křivkou). Nakonec se přepony odeberou a vznikne další iterace.

Animace vývoje:

L-systém

Výše uvedený postup lze simulovat následujícím L-systémem:

Tento L-systém je parametrický, dračí křivka však lze popsat i bezparametrickým L-systémem. Ten má tu nevýhodu, že výsledná velikost obrázku, záleží na počtu iterací (na rozdíl od prvního L-systému). Na druhou stranu se v něm nevyskytují žádná iracionální čísla, se kterými počítače neumí pracovat, proto bude aproximace velmi přesná i pro vysoké iterace.

Výsledek bude vznikat po iteracích takto:

Systémy iterovaných funkcí

Dračí křivka je také limita následujícího systému iterovaných funkcí v komplexní rovině:

${\displaystyle f_{1}(z)={(1+i)z \over 2}}$

${\displaystyle f_{2}(z)=1-{(1-i)z \over 2}.}$

Použitím dvojice reálných čísel místo komplexního dostaneme tyto dvě funkce:

${\displaystyle f_{1}(x,y)={1 \over {\sqrt {2}}}{\begin{pmatrix}\cos 45^{\circ }&-\sin 45^{\circ }\\\sin 45^{\circ }&\cos 45^{\circ }\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}}$

${\displaystyle f_{2}(x,y)={1 \over {\sqrt {2}}}{\begin{pmatrix}\cos 135^{\circ }&-\sin 135^{\circ }\\\sin 135^{\circ }&\cos 135^{\circ }\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}+{\begin{pmatrix}1\\0\end{pmatrix}}}$

Skládání papíru

Pomocí proužku papíru se dá Dračí křivka sestrojit následovně. Proužek přehýbáme napůl tak dlouho, dokud nevznikne čtverec. Poté jednotlivá složení rozevíráme, vždy ale jen o 90 stupňů.

Kód v PHP

<?php
header("Content-type: image/png");
$image=imagecreatetruecolor(800,550);
$white=imagecolorallocate($image,255,255,255);
$points=array(array(188,190),array(700,190));
for($iteration=1;$iteration<17;$iteration++){
	$oldpoints=$points;
	$points=array();
	for($i=0;$i<count($oldpoints)-1;$i++){
		$points[]=array($x1=$oldpoints[$i][0],$y1=$oldpoints[$i][1]);
		$x2=$oldpoints[$i+1][0]; $y2=$oldpoints[$i+1][1];
		if($iteration&1){
			if($y1==$y2)
				{ $x3=($x1+$x2)/2; $y3=$y1+(($x1<$x2)^($i&1)?1:-1)*abs($x1-$x2)/2; }
			else
				{ $y3=($y1+$y2)/2; $x3=$x1+(($y1<$y2)^($i&1)?-1:1)*abs($y1-$y2)/2; }
		}else{
			if ($x1<$x2 && $y1<$y2){ $x3=($i&1)?$x2:$x1; $y3=($i&1)?$y1:$y2; }
			elseif($x1<$x2 && $y1>$y2){ $x3=($i&1)?$x1:$x2; $y3=($i&1)?$y2:$y1; }
			elseif($x1>$x2 && $y1<$y2){ $x3=($i&1)?$x1:$x2; $y3=($i&1)?$y2:$y1; }
			elseif($x1>$x2 && $y1>$y2){ $x3=($i&1)?$x2:$x1; $y3=($i&1)?$y1:$y2; }
		}
		$points[]=array($x3,$y3);
	}
	$points[]=end($oldpoints);
}
for($i=0;$i<count($points)-1;$i++)
	imageline($image,$points[$i][0],$points[$i][1],$points[$i+1][0],$points[$i+1][1],$white);
imagepng($image);

Výše uvedený kód nejdříve po jednotlivých iteracích vytváří nové body (vrcholy trojúhelníků nad stávajícími úsečkami), které nakonec hromadně vykreslí. Souřadnice všech bodů si uchovává v poli, jehož velikost se zdvojnásobuje s každou iterací. Vzhledem k jednoduchosti operace se zde lze obejít bez rovnic pro obecnou rotaci geometrických útvarů. Rekurze v tomto případě též není, zásobník více méně simuluje práce s polem; program by však šel do rekurze přepsat.

Dláždění roviny

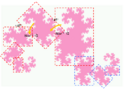
Protože Dračí křivka má vlastnosti plochu-vyplňující křivky a dá se přikládat sama k sobě tak, že části na sebe těsně dolehnou, dá se pomocí ní dláždit rovina. Na následujících obrázcích je několik způsobů dláždění.

• 

  1. krok

• 

  2. krok

• 

  3. krok

• 

  Postup

• 

  4. krok

• 

  5. krok

• 

  6. krok

• 

  Plná dračí křivka

• 

  1. krok

• 

  2. krok

• 

  3. krok

Reference

Související články

• Fraktál
• L-systém

Externí odkazy

• Obrázky, zvuky či videa k tématu Dračí křivka na Wikimedia Commons