Dynamické systémy

Dynamický systém v automatizaci je vyjadřován zpravidla diferenciálními rovnicemi, které udávají chování systému při změnách.

Dělení dynamických systémů

Statický systém

Je takový dynamický systém, v kterém na podnět vstupní veličiny dojde v konečném čase na ustálení jeho hodnot. Příkladem statického systému může být ohřev vody v konvici. Teplota vody začíná na pokojové teplotě. Pokud se změní vstupní veličina, resp. je zapnut ohřev, začíná přechodový děj, který pokračuje až do doby, než voda dosáhne 100 °C. V té chvíli se systém ustálí a hodnotu nepřesáhne. Statický systém je vyjádřen rovnici:^[1][2]

${\textstyle a_{n}{\frac {d^{n}y}{dt^{n}}}+a_{n-1}{\frac {d^{n-1}y}{dt^{n-1}}}+...+a_{1}{\frac {dy}{dt}}+a_{0}y=b_{0}u}$

Dělení podle řádů

V závislosti na rovnici daného systému jde určit řád systému.

Nultý řád

Člen nultého řádu je definován rovnicí ${\displaystyle a_{0}y=b_{0}u}$. Jedná se vlastně o proporcionální člen PID regulátoru. Z pohledu elektrotechniky se jedná o dělič napětí.^[3]

První řád

Člen prvního řádu je definován rovnicí ${\displaystyle a_{1}{\frac {d}{dt}}y+a_{0}y=b_{0}y}$. Jde o proporcionální člen se zpožděním prvního řádu. Lze si ho představit jako Integrační článek. ^[1]

Druhý řád

U takto vysokého řádu je velmi obtížné ustálit veličiny a proto se tento řád příliš nepoužívá. Do charakteristické rovnice přibude druhá derivace změny. Další důležitou věcí je, že se zde využívá koeficientu tlumení, který se vyjadřuje z přenosu systému. ^[4]

Astatické systémy

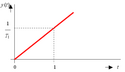
Astatické systémy jsou definovány rovnicí ${\displaystyle a_{n}{\frac {d^{n}y}{dt^{n}}}+a_{n-1}{\frac {d^{n-1}y}{dt^{n-1}}}+...+a_{1}{\frac {dy}{dt}}=b_{0}u}$. Chybí zde na levé straně prostý člen, zatímco na pravé straně je pouze prostý. Pokud je na vstup takového systému přiveden jednotkový skok, začne se výstupní veličina zvětšovat resp. se bude integrovat. To má za následek, že se tyto systémy nikdy nedokáží ustálit na ustálené hodnotě. Pokud by takovýto systém v praxi nebyl hlídán, mohlo by to zapříčinit i zničení celé soustavy. ^[5]

Integrační člen

Astatický systém tedy je integrační člen. Je definován rovnicí ${\displaystyle T_{1}y'=u}$.^[4]

Tento člen je používán pro následné stabilizování systémů. ^[6]

Reference