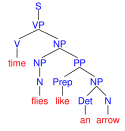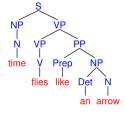Earleyův analyzátor

Earleyův algoritmus je algoritmus syntaktické analýzy, který vytvořil a v roce 1968 popsal Jay Earley ve své disertační práci^[1] vedené Robertem W. Floydem z Univerzity Carnegie-Mellon. Algoritmus byl v roce 1970 publikován ve zkrácené a čitelnější podobě v časopise Communications of the ACM^[2] v článku, zařazeném v roce 1983 mezi 21 nejvýznamnějších článků za čtvrtstoletí existence tohoto časopisu.^[3]

Původní algoritmus pouze zjišťuje, zda zadaný textový řetězec patří do jazyka popsaného bezkontextovou gramatikou – jedná se tedy o rozpoznávač (anglicky recogniser). Lze jej však rozšířit, aby v průběhu analýzy vytvářel derivační strom, čímž vznikne kompletní syntaktický analyzátor (anglicky parser).

Algoritmus je vhodný i pro nejednoznačné bezkontextové jazyky používané pro zpracování přirozeného jazyka^[4][5], díky čemuž má v matematické lingvistice podobnou úlohu jako LR parsery a LL parsery používané v matematické informatice v překladačích programovacích jazyků.

Asymptotická složitost Earleyova algoritmu pro obecný bezkontextový jazyk je O(n³), kde n je délka analyzovaného řetězce; pro jednoznačné gramatiky pracuje v kvadratickém čase O(n²)^[6], a pro téměř všechny LR(k) gramatiky v lineárním čase. Funguje obzvlášť dobře, když pravidla používají levou rekurzi. Některé varianty mohou trpět problémy s určitými vypouštějícími gramatikami^[7].

Earleyův analyzátor (anglicky Earley parser) je syntaktický analyzátor založený na Earleyově algoritmu. Často jej používají projektové frameworky podporující Rapid Application Development (RAD)^[8][9] využívané při konstrukci interpretů a kompilátorů především doménově specifických jazyků.

Princip fungování

Earleyův algoritmus patří stejně jako algoritmus CYK, do třídy tabulkových metod syntaktické analýzy (anglicky chart parsers). Při načítání řetězce zleva doprava provádí syntaktickou analýzu zdola nahoru na základě predikcí shora dolů. Výsledky jsou z dříve získaných částečných výsledků konstruovány technikou dynamického programování.

Aby se vyhnul backtrackingu, pracuje Earleyův algoritmus s množinou Earleyových položek (anglicky Earley items) nebo krátce položek, což jsou pravidla gramatiky, do jejichž pravé strany je vložena tečka, která identifikuje aktuální pozici v pravidle. Každá položka navíc obsahuje informaci, od které pozice ve vstupním řetězci se uplatní. Během práce algoritmu Earleyovy položky odrážejí dosud použitá pravidla a slouží pro predikci dalších pravidel. Analýzou vstupního řetězce, který patří do jazyka, vznikne položka, která odráží odvození řetězce z počátečního symbolu gramatiky.

Podrobný popis

V následujícím popisu se používá toto značení:

• velká písmena ze začátku abecedy A, B, atd. a symbol S reprezentují jeden neterminální symbol (S je počáteční symbol),
• X_k je jeden terminální nebo neterminální symbol,
• malá písmena t_n reprezentují jeden terminální symbol,
• malá řecká písmena α, β, γ reprezentují libovolný řetězec složený z terminálních a neterminálních symbolů (včetně prázdného řetězce označovaného ε).

Earleyovy položky

Earleyův analyzátor vytváří během analýzy každé vstupní věty tvořené symboly t₁ … t_n (n je délka vstupní věty) specifickou množinu Earleyových položek.

Vstupní pozice i je pozice za i-tým symbolem vstupní věty; před načtením prvního symbolu je vstupní pozice 0.

Earleyova položka pro pravidlo gramatiky A → X₁ … X_q je výraz tvaru [A →_h X₁ … X_p •_i X_{p + 1} … X_q], přičemž tečka může být v libovolném místě počínaje pozicí bezprostředně před X₁ až po pozici bezprostředně za X_q, tj. 0 ≤ p ≤ q, index h u šipky udává, na které vstupní pozici začíná část vstupní věty vygenerovaná pravidlem odpovídajícím právě probírané položce, index i u tečky je pozice za posledním dosud načteným terminálním symbolem; platí tedy 0 ≤ h ≤ i ≤ n.

Algoritmus

Před analýzou každé věty se množina Earleyových položek vždy inicializuje jedinou položkou [S’ →₀ •₀ S], kde S je počáteční symbol dané gramatiky, a S’ je přidaný pomocný počáteční symbol.

Analyzátor opakovaně provádí tři operace: predikci, načtení a kompletaci, které do množiny Earleyových položek přidávají nové položky na základě existujících položek a vstupního řetězce:

• Predikce (anglicky prediction) přidává položky, odpovídající dalším očekáváním analyzátoru shora dolů: pro každou položku [A →_h X₁ … X_p •_i X_p+1 … X_q], která má za tečkou neterminální symbol, tj. X_p+1 je neterminál B, a pro každé pravidlo B → β, které má tento neterminál na levé straně, se do množiny pravidel přidá položka [B →_i •_i β].
• Načtení (anglicky scanning) je načtení terminálního symbolu shodného s očekáváním analyzátoru shora dolů: Jestliže t_i+1 je první dosud nenačtený symbol ve vstupním řetězci, pak pro každou položku [A →_h α •_i t_i+1η], která má tento symbol bezprostředně za tečkou, přidáme položku [A →_h αt_i+1 •_i+1 η].
• Kompletace (anglicky completion) realizuje část analýzy zdola nahoru: Pro každou kompletní položku, to jest položku tvaru [A →_h α •_i], která má tečku na konci, a položku, která má neterminál z levé strany této položky bezprostředně za tečkou [B →_g β •_h Aγ], přidáme položku [B →_g βA •_i γ], v níž je tečka přesunuta za neterminál A a index u ní je změněn na i.

Uvedené operace se opakují tak dlouho, dokud přibývají nové položky. Pokud nově utvořená položka v množině již je, nebudeme ji přidávat. Množina je zpravidla implementována jako fronta položek, které se mají zpracovat, s operacemi, které se mají provádět podle toho, o jaký druh položky se jedná.

Původní Earleyův algoritmus zahrnoval do položky i náhled; pozdější výzkum ukázal, že náhled má malý praktický vliv na efektivitu analýzy a proto jej většina implementací nepoužívá.

Alternativní zápis

Earleyovy položky se někdy rozdělují podle vstupní pozice (tj. indexu za tečkou) do různých množin označovaných S(i), kde i je vstupní pozice. Počáteční pozice položky (h) se pak obvykle nepíše jako index u šipky, ale do závorek, ve kterých je položka zapsána: (A → X₁ … X_p • X_{p + 1} … X_q, h).

Analyzátor začíná s množinou položek S(0) obsahující jedinou položku (S’ → • S, 0), kde S je vlastní počáteční symbol dané gramatiky, a S’ je přidaný pomocný počáteční symbol. Operace predikci, načtení a kompletaci lze pak popsat takto:

• Predikce: pokud v S(i) existuje položka tvaru (X → α • B β, h) (kde h je počáteční pozice definovaná výše) s terminálním symbolem bezprostředně za tečkou, pak projdeme všechna pravidla, která mají tento symbol B na levé straně a do S(i) přidáme pro každé pravidlo tvaru (B → β) položku (B → • β, i).
• Načtení: jestliže další symbol ve vstupním řetězci je t_i+1, pro každou položku v S(i) tvaru (X → α • t_i+1 β, h), přidáme (X → α t_i+1 • β, h) do S(i+1).
• Kompletace: pro každou položku v S(i) tvaru (A → α •, h), najdeme v S(h) položky tvaru (B → β • A γ, g), a přidáme (B → β A • γ, i) do S(i).

Pseudokód

Pseudokód je převzatý z publikace^[10], kterou napsal Daniel Jurafsky a James H. Martin. Earleyovy položky se nazývají state, jejich množina je S; predikát FINISHED je pravdivý, pokud tečka v položce je na konci pravé strany, funkce NEXT_ELEMENT_OF vrací první symbol za tečkou, počáteční symbol je #.

DECLARE ARRAY S;

function INIT(words)
    S ← CREATE_ARRAY(LENGTH(words) + 1)
    for k ← from 0 to LENGTH(words) do
        S[k] ← EMPTY_ORDERED_SET

function EARLEY_PARSE(words, grammar)
    INIT(words)
    ADD_TO_SET((# → •S, 0), S[0])
    for k ← from 0 to LENGTH(words) do
        for each state in S[k] do  { S[k] se v této smyčce může zvětšovat }
            if not FINISHED(state) then
                if NEXT_ELEMENT_OF(state) is a nonterminal then
                    PREDICTOR(state, k, grammar)         { neterminál }
                else do
                    SCANNER(state, k, words)             { terminál }
            else do
                COMPLETER(state, k)
        end
    end
    return chart

procedure PREDICTOR((A → α•Bβ, j), k, grammar)
    for each (B → γ) in GRAMMAR_RULES_FOR(B, grammar) do
        ADD_TO_SET((B → •γ, k), S[k])
    end

procedure SCANNER((A → α•aβ, j), k, words)
    if a ⊂ PARTS_OF_SPEECH(words[k]) then
        ADD_TO_SET((A → αa•β, j), S[k+1])
    end

procedure COMPLETER((B → γ•, x), k)
    for each (A → α•Bβ, j) in S[x] do
        ADD_TO_SET((A → αB•β, j), S[k])
    end

Příklad

Analýza anglických vět

Pro „mikrogramatiku” angličtiny

S → NP VP

NP → Det N

NP → Det Adj N

VP → V

VP → V NP

a vstupní řetězec The_Det black_Adj cat_N ate_V a_Det white_Adj mouse_N vytváří algoritmus následující množiny Earleyových položek:

Earleyova položka	Zdroj přidání do množiny položek
[S’ →0 •0 S]	inicializace
[S →0 •0 NP VP]	predikce S z položky [S’ →0 •0 S]
[NP →0 •0 Det N]	predikce NP z položky [S →0 •0 NP VP]
[NP →0 •0 Det Adj N]	predikce NP z položky [S →0 •0 NP VP]
[NP →0 Det •1 N]	načtení Det z položky [NP →0 •0 Det N]
[NP →0 Det •1 Adj N]	načtení Det z položky [NP →0 •0 Det Adj N]
[NP →0 Det Adj •2 N]	načtení Adj z položky [NP →0 Det •1 Adj N]
[NP →0 Det Adj N •3]	načtení N z položky [NP →0 Det Adj •2 N]
[S →0 NP •3 VP]	kompletace NP z položky [S0 → •0 NP VP]
[VP →3 •3 V]	predikce VP z položky [S →0 NP •3 VP]
[VP →3 •3 V NP]	predikce VP z položky [S →0 NP •3 VP]
[VP →3 V •4]	načtení V z položky [VP →3 •3 V]
[VP →3 V •4 NP]	načtení V z položky [VP →3 •3 V NP]
[S →0 NP VP •4]	kompletace VP z položky [S →0 NP •3 VP]
[NP →4 •4 Det N]	predikce NP z položky [VP →3 V •4 NP]
[NP →4 •4 Det Adj N]	predikce NP z položky [VP →3 V •4 NP]
[S’ →0 S •4]	kompletace S z položky [S’ →0 •0 S]
[NP →4 Det •5 N]	načtení Det z položky [NP →4 •4 Det N]
[NP →4 Det •5 Adj N]	načtení Det z položky [NP →4 •4 Det Adj N]
[NP →4 Det Adj •6 N]	načtení Adj z položky [NP →4 Det •5 Adj N]
[NP →4 Det Adj N •7]	načtení N z položky [NP →4 Det Adj •6 N]
[VP →3 V NP •7]	kompletace NP z položky [VP →3 V •4 NP]
[S →0 NP VP •7]	kompletace VP z položky [S →0 NP •3 VP]
[S’ →0 S •7]	kompletace S z položky [S’ →0 •0 S]

Poslední Earleyova položka [S’ →₀ S •₇] odpovídá úplnému odvození celého vstupního řetězce. Earleyova položka [S’ →₀ S •₄] ukazuje, že první čtyři symboly tohoto řetězce také tvoří správnou větu dané gramatiky.

Příklady

Analýza aritmetických výrazů

Uvažujme následující jednoduchou gramatiku pro aritmetické výrazy:

<P> ::= <S> # počáteční pravidlo
<S> ::= <S> "+" <M> | <M>
<M> ::= <M> "*" <T> | <T>
<T> ::= "1" | "2" | "3" | "4"

Při analýze vstupního řetězce:

2 + 3 * 4

dostáváme následující posloupnost množin položek (i je číslo položky a p je počáteční pozice):

(i) Pravidlo         (p)    # Komentář
--------------------------------------------------------

S(0): • 2 + 3 * 4

(1)  P → • S         (0)    # počáteční pravidlo
(2)  S → • S + M     (0)    # predikce z (1)
(3)  S → • M         (0)    # predikce z (1)
(4)  M → • M * T     (0)    # predikce z (3)
(5)  M → • T         (0)    # predikce z (3)
(6)  T → • číslo     (0)    # predikce z (5)

S(1): 2 • + 3 * 4

(1)  T → číslo •     (0)    # načtení z S(0)(6)
(2)  M → T •         (0)    # kompletace z (1) a S(0)(5)
(3)  M → M • * T     (0)    # kompletace z (2) a S(0)(4)
(4)  S → M •         (0)    # kompletace z (2) a S(0)(3)
(5)  S → S • + M     (0)    # kompletace z (4) a S(0)(2)
(6)  P → S •         (0)    # kompletace z (4) a S(0)(1)

S(2): 2 + • 3 * 4

(1)  S → S + • M     (0)    # načtení z S(1)(5)
(2)  M → • M * T     (2)    # predikce z (1)
(3)  M → • T         (2)    # predikce z (1)
(4)  T → • číslo     (2)    # predikce z (3)

S(3): 2 + 3 • * 4

(1)  T → číslo •     (2)    # načtení z S(2)(4)
(2)  M → T •         (2)    # kompletace z (1) a S(2)(3)
(3)  M → M • * T     (2)    # kompletace z (2) a S(2)(2)
(4)  S → S + M •     (0)    # kompletace z (2) a S(2)(1)
(5)  S → S • + M     (0)    # kompletace z (4) a S(0)(2)
(6)  P → S •         (0)    # kompletace z (4) a S(0)(1)

S(4): 2 + 3 * • 4

(1)  M → M * • T     (2)    # načtení z S(3)(3)
(2)  T → • číslo     (4)    # predikce z (1)

S(5): 2 + 3 * 4 •

(1)  T → číslo •     (4)    # načtení z S(4)(2)
(2)  M → M * T •     (2)    # kompletace z (1) a S(4)(1)
(3)  M → M • * T     (2)    # kompletace z (2) a S(2)(2)
(4)  S → S + M •     (0)    # kompletace z (2) a S(2)(1)
(5)  S → S • + M     (0)    # kompletace z (4) a S(0)(2)
(6)  P → S •         (0)    # kompletace z (4) a S(0)(1)

Výskyt položky (P → S •, 0) v množině znamená, že načtený řetězec patří do jazyka. Tato položka se také objevuje v S(3) a S(1), což jsou úplné věty.

Výpočetní složitost

Pokud implementace Earleyova algoritmu používá seznam množin a ignoruje index nezpracovaného vstupního symbolu v položkách, může prohlížet množiny z tohoto seznamu postupně, díky čemuž inkrementálně analyzuje vstupní symboly t_i pro rostoucí index i.

Earleyovy položky v množině se obvykle prohlíží v tom pořadí, v jakém byly přidávány, každá pouze jednou. Pokud má algoritmus správně fungovat pro gramatiky obsahující pravidla s prázdnou pravou stranou, musí být upraven, jak je uvedeno dále. Pro procházení množiny položek stačí fronta, pro efektivní kontrolu, že fronta danou položku dosud neobsahuje, je vhodné položky z každé fronty umístit do asociativního pole. Efektivní kompletace položek, které nemají tečku na konci pravidla, vyžaduje ještě jedno asociativní pole, které obsahuje seznamy takových položek; klíčem je dvojice (X_p, i), složená ze symbolu ležícího v těchto položkách bezprostředně za tečkou a z indexu nezpracovaného terminálního symbolu. Pro efektivní predikci nové položky je třeba s každým neterminálním symbolem také svázat seznam všech pravidel, jejichž levou stranu tvoří tento symbol.

Pokud se jako výše zmíněné asociativní pole použije hašovací tabulka, pak krok zahrnující konstrukci nové Earleyovy položky a pokus o její přidání do množiny položek lze vykonat s asymptotickou složitostí O(1).

Earley ve svém článku^[2] ukázal, že v obecném případě:

• i-tá množina obsahuje O(i) položek, protože jejich počet lze omezit součinem počtu možných hodnot indexu h (závislým na i), počtu pravidel a počtu možných umístění tečky na jejich pravých stranách (poslední dva činitelé jsou konstanty závislé na dané gramatice, ale nezávislé na i);
• provedení načtení nebo predikce znamená O(1) kroků pro každou Earleyovu položku v libovolné množině, tedy v i-té množině položek se provede O(i) kroků;
• akce kompletace provádí O(i) kroků pro každou zpracovanou položku, protože v nejhorším případě se přidává O(h) položek patřících do h-té množiny, přičemž h = O(i), takže v i-té množině položek se provede O(i²) kroků;
• sečtením pro i od 0 do n dostaneme pro celkový počet kroků O(n³) a pro počet položek O(n²).

Ve stejném článku je také dokázáno, že pro jednoznačné gramatiky akce kompletace provádí v i-té množině položek O(i) kroků, což dává kvadratickou složitost algoritmu, a že třída gramatik, pro které Earleyův algoritmus funguje v lineárním čase, pokrývá všechny gramatiky, u nichž lze počet položek v každé množině shora omezit konstantou. Do této třídy naleží právě všechny gramatiky LR(k), kromě některých gramatik s pravou rekurzí, což jsou gramatiky většiny programovacích jazyků.

Earleyův algoritmus funguje obzvlášť efektivně pro gramatiky s levou rekurzí. Uvažujme například analýzu řetězce aaa v gramatice

S → Sa

S → a

Earleyův algoritmus tvoří následující položky:

Earleyova položka	Zdroj přidání do množiny položek
[S’ →0 •0 S]	inicializace
[S →0 •0 Sa]	predikce S z položky [S’ →0 •0 S], a pak z položky [S →0 •0 Sa]
[S →0 •0 a]	predikce S z položky [S’ →0 •0 S], a pak z položky [S →0 •0 Sa]
[S →0 a •1]	načtení a z položky [S →0 •0 a]
[S’ →0 S •1]	kompletace S z položky [S’ →0 •0 S]
[S →0 S •1 a]	kompletace S z položky [S →0 •0 Sa]
[S →0 Sa •2]	načtení a z položky [S →0 S •1 a]
[S’ →0 S •2]	kompletace S z položky [S’ →0 •0 S]
[S →0 S •2 a]	kompletace S z položky [S →0 •0 Sa]
[S →0 Sa •3]	načtení a z položky [0S → S •2 a]
[S’ →0 S •3]	kompletace S z položky [S’ →0 •0 S]
[S →0 S •3 a]	kompletace S z položky [S →0 •0 Sa]

Počet položek pro každou hodnotu indexu u tečky je 3, takže algoritmus funguje v lineárním čase.

Pro porovnaní použití gramatiky s pravou rekurzí

S → aS

S → a

pro analýzu téhož řetězce aaa vede k vytvoření následujících Earleyových položek:

Earleyova položka	Zdroj přidání do množiny položek
[S’ →0 •0 S]	inicializace
[S →0 •0 aS]	predikce S z položky [S’ →0 •0 S]
[S →0 •0 a]	predikce S z položky [S’ →0 •0 S]
[S →0 a •1 S]	načtení a z položky [S’ →0 •0 aS]
[S →0 a •1]	načtení a z položky [S’ →0 •0 a]
[S →1 •1 aS]	predikce S z položky [S →0 a •1 S]
[S →1 •1 a]	predikce S z položky [S →0 a •1 S]
[S’ →0 S •1]	kompletace S z položky [S’ →0 •0 S]
[S →1 a •2 S]	načtení a z položky [S’ →1 •1 aS]
[S →1 a •2]	načtení a z položky [S’ →1 •1 a]
[S →2 •2 aS]	predikce S z položky [S →1 a •2 S]
[S →2 •2 a]	predikce S z položky [S →1 a •2 S]
[S →0 aS •2]	kompletace S z položky [S’ →0 a •1 S]
[S’ →0 S •2]	kompletace S z položky [S’ →0 •0 S]
[S →2 a •3 S]	načtení a z položky [S’ →2 •2 aS]
[S →2 a •3]	načtení a z položky [S’ →2 •2 a]
[S →3 •3 aS]	predikce S z položky [S →2 a •3 S]
[S →3 •3 a]	predikce S z položky [S →2 a •3 S]
[S →1 aS •3]	kompletace S z položky [S’ →1 a •2 S]
[S →0 aS •3]	kompletace S z položky [S’ →0 a •1 S]
[S’ →0 S •3]	kompletace S z položky [S’ →0 •0 S]

Počet položek s danou hodnotou indexu u tečky roste lineárně se zvětšováním tohoto indexu; algoritmus má pro tyto gramatiky kvadratickou časovou složitost.

Prázdná pravidla

Pokud Earleyův algoritmus prochází položky z i-té množiny pouze jednou a v pořadí, v jakém byly přidávány, pak může fungovat nesprávně pro gramatiky, které obsahují pravidla s prázdnou pravou stranou (nazývané také ε-pravidla, protože ε tradičně označuje prázdný řetězec symbolů gramatiky). Při kompletaci položky [E →_i •_i], která odpovídá prázdnému pravidlu E → ε, je třeba prohlédnout i právě vytvářenou i-tou množinu. Pokud položka [X →_h α •_i Eη] bude do ní přidána až po kompletaci položek [E →_i •_i], pak kompletace nikdy nepřidá položku [X →_h αE •_i η]. Nebudou také přidány žádné položky přímo i nepřímo z ní vyplývající. To může vést k odmítnutí správného vstupního řetězce, jak ukazuje následující příklad použití gramatiky

S → E A A A

A → E

E → ε

pro analýzu prázdného řetězce ε. V množině Earleyových položek jsou červeně označeny položky, které algoritmus měl přidat do množiny, ale nepřidal.

Earleyova položka	Zdroj přidání do množiny položek
[S’ →0 •0 S]	inicializace
[S →0 •0 E A A A]	predikce S z položky [S’ →0 •0 S]
[E →0 •0]	predikce E z položky [S →0 •0 E A A A]
[S →0 E •0 A A A]	kompletace E z položky [S →0 •0 E A A A]
[A →0 •0 E]	predikce A z položky [S →0 E •0 A A A]
[A →0 E •0]	ne kompletace E z položky [A →0 •0 E]
[S →0 E A •0 A A]	ne kompletace A z položky [S →0 E •0 A A A]
[S →0 E A A •0 A]	ne kompletace A z položky [S →0 E A •0 A A]
[S →0 E A A A •0]	ne kompletace A z položky [S →0 E A A •0 A]
[S’ →0 S •0]	ne kompletace S z položky [S’ →0 •0 S]

Bylo publikováno několik řešení tohoto problému:

• A. V. Aho a J. D. Ullman^[11] doporučují opakovaně procházet smyčkou predikce a kompletace všech položek z i-té množiny tak dlouho, dokud postupné iterace zvětšují její velikost;
• Earley^[2] navrhl pamatovat si při kompletaci položek neterminální symboly, z nichž lze vyprodukovat prázdný řetězec (anglicky nullable symbols); tyto symboly se poznají tak, že stojí na levé straně pravidla s prázdnou pravou stranou nebo složeného jen ze symbolů přepsatelných na prázdný řetězec, a při doplňování do množiny položek [A →_h α •_i Bη], pokud ze symbolu B stojícího po tečce se dá vyprodukovat prázdný řetězec, doplníme do množiny také položku [A →_h αB •_i η];
• podobné řešení J. Aycocka a R. N. Horspoola^[12] spočívá v změně predikce položek na „pokud existuje položka [A →_h α •_i Bη], pak pro každé pravidlo B → β přidej položku [B →_i •_i β]; pokud ze symbolu B lze vyprodukovat prázdný řetězec, pak přidej také položku [A →_h αB •_i η]”, přičemž množinu neterminálních symbolů přepsatelných na prázdný řetězec lze snadno stanovit předem;
• každou gramatiku, z jejíhož počátečního symbolu se nedá vyprodukovat prázdný řetězec, lze upravit na ekvivalentní gramatiku bez prázdných pravidel^[13].

Rozšíření algoritmu pro syntaktickou analýzu

Výše popsaný algoritmus pouze rozpoznává, zda daný řetězec terminálních symbolů tvoří správnou větu dané bezkontextové gramatiky (takový algoritmus se anglicky nazývá recognizer), ale nevytváří syntaktický strom. Bylo navrženo několik způsobů rozšíření algoritmu na analyzátor. Komplikaci představuje počet derivačních stromů, který může být až exponenciální funkcí délky vstupní věty, a pro gramatiky s cykly může být i nekonečný. Existují však způsoby kódování všech derivačních stromů pomocí datových struktur o velikosti, která je polynomiální funkcí délky vstupní věty.

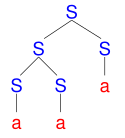
Správné derivační stromy řetězce aaa
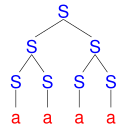
Chybné derivační stromy řetězce aaa

V Earleyových článcích^[1][2] je stručně popsáno, jak rozšířit algoritmus rozpoznávání na analyzátor přidáním ukazatele ke každému neterminálnímu symbolu na pravé straně pravidel v položkách Earleyovy množiny, který bude ukazovat na položku, jež způsobila kompletaci tohoto symbolu: při každé kompletaci, při které vznikne položka tvaru [B →_g βA •_i γ] se tvoří ukazatel na položku [A →_h α •_i]. M. Tomita^[14][15] však upozornil, že se při tom neuvažují vztahy mezi symboly, takže pro gramatiku

S → S S

S → a

parser navržený Earleyem při analýze vstupního řetězce aaa vrátí nejen správné derivační stromy řetězce aaa, ale také derivační stromy, které odpovídají řetězcům aa a aaaa.

Tomu je možné zabránit různými způsoby; je relativně jednoduché vzít úplné položky z tabulky, prohledat je shora dolů a pro vytvoření derivačního lesa použít pouze ty, které patří k sobě. Jiná možnost je doplnit položky [B →_g βA •_i γ] vzniklé kompletací ne jedním, ale dvojicí ukazatelů: do položky [B →_g β •_h Aγ] i do položky [A →_h α •_i]. Naivní aplikace této myšlenky doplněním uvedených dvojic ukazatelů do sady návěstí rozlišujících položky však může vést ke zvýšení časové složitosti nad n³, což ukázal M. Johnson^[16] následujícím příkladem: pro gramatiku

S → S … S (m + 2 opakování symbolu S)

S → S S

S → a

analyzuje Earleyův algoritmus s takto definovanými položkami vstupní řetězec a … a (n + 1 opakování symbolu a, přičemž n > m) v čase Ω(n^m).

V. A. Lapšin^[17] navrhl ukládat množiny takovýchto dvojic ukazatelů v asociativním poli, v němž budou klíčem Earleyovy položky, spolu s algoritmem vytváření derivačních stromů z tabulky položek za použití těchto ukazatelů. Časová složitost tohoto analyzátoru bez budovaní derivačního stromu nepřekračuje řád n³.

E. Scottová^[18] publikovala jiný algoritmus, který v čase O(n³) doplňuje Earleyovy položky ukazatelem na uzel společně baleného lesa analýzy (anglicky shared packed parse forest, SPPF) používaného v GLR analyzátorech, v nichž každý uzel má nejvýše dva syny. Každá Earleyova položka je rozšířena o ukazatel na uzel sdíleného pakovaného derivačního lesa označený trojicí (s, i, j), kde s je symbol nebo LR(0) položka (tj. přepisovací pravidlo s tečkou) a i a j udávají, jaká část vstupního řetězce je generována tímto uzlem. Obsahem uzlu je buď dvojice ukazatelů na potomka udávajících jedinou derivaci, nebo seznam „pakovaných“ uzlů, z nichž každý obsahuje dvojici ukazatelů a reprezentuje jednu derivaci. SPPF uzly jsou unikátní (existuje vždy pouze jeden s daným označením), ale pro nejednoznačné analýzy mohou obsahovat více než jednu derivaci. Takže i kdyby určitá operace nepřidala Earleyovu položku (protože už existuje), stále může přidat derivaci k derivačnímu lesu položky. Platí:

• Predikované položky mají nulový SPPF ukazatel.
• Analyzátor vytváří SPPF uzel reprezentující neterminál, který právě analyzuje.
• Když pak analyzátor nebo completer posouvá položku vpřed, přidá derivaci, jejíž potomci jsou uzlem z položky, jejíž tečka byla posunuta vpřed a jeden pro nový symbol, přes který byl posunut vpřed (neterminál nebo dokončená položka).
• SPPF uzly nejsou nikdy označeny dokončenou LR(0) položkou ale vytvořeným symbolem, takže všechna odvození jsou zkombinovaná pod jeden uzel bez ohledu na to, ze kterého přepisovacího pravidla pocházejí.

D. Grune a C. J. H. Jacobs^[19] navrhli metodu konstrukce derivačního stromu z množiny položek za pomocí Ungerova syntaktického analyzátoru.

Náhled terminálních symbolů

Operace predikce v Earleyově algoritmu může využívat náhled (anglicky lookahead). Pak funguje takto: „pokud existuje položka [A →_h α •_i Bη], pak pro každé pravidlo B → β přidej položku [B →_i •_i β], pokud množina FIRST řetězců symbolu β obsahuje terminální symbol t_i”. Jako obvykle při používání náhledu, je vhodné umístit na konec analyzovaného řetězce symbolů zarážku t_n = $, která nepatří do množiny terminálních symbolů.

V původním Earleyově článku^[2] bylo navrženo používání náhledu také v operacích kompletace. Na rozdíl od predikce se při kompletaci nedá předem stanovit množina přípustných nástupců, pokud se nebere v úvahu jeho méně efektivní a omezená verze založená na množinách FOLLOW. Efektivní náhled při kompletaci spočívá v následujících modifikacích algoritmu:

• množina přípustných nástupců počáteční položky [S’ →₀ •₀ S] má jeden prvek – zarážku $;
• při operaci načtení nově vzniklá položka [A →_h αt_i •_i+1 η] dědí množinu přípustných nástupců svého předchůdce [A →_h α •_i t_iη];
• při operaci predikce položka [B →_i •_i β] na základě položky [A →_h α •_i Bη] o množině přípustných nástupců N_A zjistíme přípustné nástupce nově vzniklé položky jako množinu FIRST(Bη), pokud FIRST(Bη) neobsahuje prázdný symbol ε; nebo jako sumu množin FIRST(Bη) ∪ N_A, pokud FIRST(Bη) prázdný symbol ε obsahuje;
• při operaci kompletace položky [A →_h α •_i] se nová položka [B →_g βA •_i γ] přidává jen tehdy, pokud množina přípustných nástupců položek [A →_h α •_i] obsahuje i-tý terminální symbol t_i.

Je možné také používat náhled více než jednoho terminálního symbolu.

Varianty Earleyova algoritmu s náhledem používajícím různý počet symbolů při predikci a kompletaci studovali M. Bouckaert, A. Pirotte a M. Snelling^[20], kteří simulacemi zjistili, že nejlepší výsledky přináší náhled jednoho symbolu při predikci, který zmenšuje počty položek o 20–50% oproti verzi bez náhledu. Používání jakéhokoli náhledu při kompletaci však má větší režii než zisk z něho plynoucí. Mnoho implementací Earleyova algoritmu vůbec náhled nepoužívá, takže používají přímo danou gramatiku bez předzpracovávání spočívajícím v nalezení množin FIRST.

Modifikace algoritmu

F. C. N. Pereira a D. H. D. Warren ukázali^[21], jak zobecnit tabulkové metody syntaktické analýzy pro libovolné gramatické formalismy založené na unifikaci, včetně kontextových. Zahájil vlnu článků popisujících verze Earleyova algoritmu pro formalismus unifikací PATR-II^[22], pro gramatiky se vkládáním stromů (anglicky Tree Adjoining Grammar, TAG)^[23][24], S-atributové gramatiky (anglicky S-attribute grammar)^[25], hypergrafové gramatiky (anglicky hypergraph grammar)^[26], sekvenčně indexované gramatiky (anglicky sequentially indexed grammars)^[27] atd. Technika magických množin (anglicky magic sets)^[28] v deduktivních databázích je také založena na myšlenkách Pereiry a Warrena.

S. L. Graham a M. A. Harrison^[29] poukázali na společné rysy Earleyova algoritmu a algoritmu CYK a společně s V. R. Ruzzem vytvořili algoritmus syntaktické analýzy, který je hybridem těchto dvou algoritmů^[30].

J. Aycock a N. Horspool^[12][31] ukázali, jak zkonstruovat deterministický konečný automat podobný analyzátoru LR(0), který analyzuje vstupní data několikanásobně rychleji než tradiční implementace Earleyova algoritmu.

A. Päseler^[32] vytvořila variantu Earleyova algoritmu, která místo seznamů terminálních symbolů analyzuje mřížky slov (anglicky word lattice). Mřížky slov jsou užitečné při rozpoznávání řeči a analýze textů psaných bez mezer mezi výrazy, např. v jazycích Dálného východu.

A. Stolcke^[33] publikoval algoritmus, který vrací nejpravděpodobnější syntaktickou analýzu vstupního řetězce pro danou pravděpodobnostní bezkontextovou gramatiku.

G. Lyon^[34] a B. Langa^[35] vytvořil varianty Earleyova algoritmu, které fungují pro vstupní věty s chybějícími, nadbytečnými nebo neznámými fragmenty.

Zdrojový kód

V polských wikizdrojích je zdrojový kód Earleyova analyzátoru v jazyce Python, který pracuje bez náhledu, zpracovává prázdná pravidla podle Earleyova návrhu^[2], a vytváří syntaktické stromy podle Lapšinova návrhu^[17]. Výstupem programu jsou všechny syntaktické stromy pro zadaný vstupní řetězec zapsané v závorkové notaci.

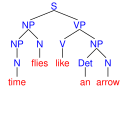
Tento program nalezne čtyři derivační stromy nejednoznačné věty time flies like an arrow. Výsledek vykreslený pomocí programu phpSyntaxTree^[36] vypadá takto:

časové mouchy mají rády šíp	čas letí jako šíp	měř čas much podobných šípu	měř čas much jako šíp
Derivační stromy věty time flies like an arrow

Odkazy

Reference

V tomto článku byly použity překlady textů z článků Earley parser na anglické Wikipedii a Algorytm Earleya na polské Wikipedii.

Související články

• Algoritmus Cocke-Younger-Kasami (CYK algoritmus)
• Bezkontextová gramatika

Externí odkazy

• AYCOCK, John; HORSPOOL, R. Nigel. Practical Earley Parsing. 6. vyd. Svazek 45. [s.l.]: [s.n.], 2002. DOI 10.1093/comjnl/45.6.620. 
• LEO, Joop M. I. M. A general context-free parsing algorithm running in linear time on every LR(k) grammar without using lookahead. 1. vyd. Svazek 82. [s.l.]: [s.n.], 1991. DOI 10.1016/0304-3975(91)90180-. .

• TOMITA, Masaru. LR parsers for natural languages. In: 10th International Conference on Computational Linguistics. [s.l.]: [s.n.], 1984. Dostupné online.

• ŽELEZNÝ, Miloš. Strukturální metody rozpoznávání [online]. Plzeň: Katedra kybernetiky ZČU. Dostupné online. 

Implementace

Implementace pro jazyk C/C++

• 'Earley Parser' Earleyův analyzátor pro jazyk C - knihovna.
• 'C Earley Parser' Earleyův analyzátor pro jazyk C.

Implementace pro jazyk Haskell

• 'Earley' Earleyův analyzátor DSL v jazyce Haskell

Implementace pro jazyk Java

• PEN Java knihovna, která implementuje Earleyův algoritmus.
• Pep Java knihovna, která implementuje Earleyův algoritmus a při analýze vytváří tabulky a derivační stromy.
• [1] Java implementace Earleyova analyzátoru.
• digitalheir/java-probabilistic-earley-parser - knihovna pro jazyk Java implementující pravděpodobnostní Earleyův algoritmus, což je užitečné pro výběr nejpravděpodobnějšího odvození nejednoznačné věty

Implementace pro jazyk C#

• coonsta/earley Earleyův analyzátor v jazyce C#
• patrickhuber/pliant Earleyův analyzátor zahrnující vylepšení z analyzátoru Marpa s vyvářením stromu podle Elizabeth Scott.
• ellisonch/CFGLib PCFG Knihovna implementující pravděpodobnostní Earleyův analyzátor pro C# (Earley + SPPF, CYK)

Implementace pro JavaScript

• 'JavaScript Moony Parser' Earleyův analyzátoru napsaný v JavaScriptu.
• Nearley Earleyův analyzátor obsahující část vylepšení použitých v analyzátoru Marpa.
• [2] Implementace v jazyce JavaScript++.

Implementace pro OCaml

• Simple Earley Implementace jednoduchého analyzátoru ve stylu Earleyova analyzátoru s dokumentací.

Implementace pro jazyk Perl

• Marpa::R2, Perlový modul. Marpa Archivováno 7. 3. 2013 na Wayback Machine. je Earleyův algoritmus zahrnující vylepšení, která navrhli Joop Leo, Aycock a Horspool.
• Parse::Earley Perlový modul, který implementuje původní algoritmus Jay Earleye.

Implementace pro jazyk Python

• Lark Objektově orientovaná implementace Earleyova analyzátoru na méně 200 řádcích kódu.
• Charty Implementace Earleyova analyzátoru pro Python.
• NLTK Toolkit pro Python, který obsahuje Earleyův analyzátor.
• Spark Objektově orientovaný „malý jazykový framework“ pro Python, který implementuje Earleyův analyzátor.
• spark_parser Aktualizovaná verze analyzátoru Spark z předchozího odkazu, která funguje na Pythonu 3 i Pythonu 2
• earley3.py Samostatná implementace algoritmu s méně než 150 řádky kódu, včetně generování lesa analýzy a příkladů.
• tjr_python_earley_parser Minimalistický Earleyův analyzátor v Pythonu.

Implementace pro jazyk Common Lisp

• CL-EARLEY-PARSER Knihovna pro Common Lisp, která implementuje Earleyův analyzátor.

Implementace pro jazyk Scheme/Racket

• Charty-Racket Implementace Earleyova analyzátoru pro jazyky Scheme / Racket.

Další nástroje

• Překladač překladačů Accent Archivováno 18. 7. 2011 na Wayback Machine.