Ekvipartiční teorém

Ekvipartiční teorém v termodynamice kvantitativně spojuje teplotu systému s průměrnou energií jednotlivých stupňů volnosti. Lze jej použít obecně pro libovolný klasický systém v termodynamické rovnováze. Předpokladem je, že mezi jednotlivými stupni volnosti je umožněna výměna energie, což je vlastnost systému zvaná ergodicita. Slovo „ekvipartiční“ znamená rovnoměrné dělení, takže ekvipartiční teorém ve zjednodušené formě říká, že na každý stupeň volnosti připadá stejná průměrná energie. Například v jednoatomovém ideálním plynu připadá na každý atom průměrná kinetická energie ${\displaystyle {\frac {3}{2}}kT}$, kde ${\displaystyle T}$ je termodynamická teplota plynu a ${\displaystyle k}$ je Boltzmannova konstanta. Počet stupňů volnosti atomu je 3, takže na každý stupeň volnosti připadá v průměru energie ${\displaystyle {\frac {1}{2}}kT}$. Právě takový příspěvek vyplývá z ekvipartičního teorému. Důležité přitom je, že kinetická energie částice závisí na druhé mocnině rychlosti (${\displaystyle E_{\mathrm {k} }={\frac {1}{2}}mv^{2}}$, kde ${\displaystyle m}$ je hmotnost částice). Průměrná energie stupňů volnosti, které přispívají k energii kvadraticky, je právě ${\displaystyle {\frac {1}{2}}kT}$. Tato jednoduchá poučka má velmi široké využití a lze ji dále zobecnit. Nesouhlas některých předpovědí ekvipartičního teorému s experimenty se stal počátkem 20. století významnou motivací pro vznik kvantové teorie.

Formulace

Ekvipartiční teorém v obecném případě říká, že pro systém v termodynamické rovnováze platí za určitých předpokladů pro každé dva indexy ${\displaystyle m,n}$:

${\displaystyle {\Bigl \langle }x_{m}{\frac {\partial H}{\partial x_{n}}}{\Bigr \rangle }=\delta _{mn}kT\,,}$

kde ${\displaystyle H}$ je Hamiltonova funkce popisující celkovou energii systému, ${\displaystyle x_{n}}$ jsou kanonické proměnné (souřadnice ve fázovém prostoru), ${\displaystyle \delta _{mn}}$ je Kroneckerovo delta, ${\displaystyle k}$ je Boltzmannova konstanta, ${\displaystyle T}$ je termodynamická teplota. Průměrem ${\displaystyle <\dots >}$ se rozumí časová střední hodnota.

Například pokud se určitý stupeň volnosti objevuje v hamiltoniánu jen jako kvadratický člen ${\displaystyle a_{n}x_{n}^{2}}$, kde ${\displaystyle x_{n}}$ je n-tá kanonická proměnná (zobecněná souřadnice nebo hybnost), pak

${\displaystyle kT={\Bigl \langle }x_{n}{\frac {\partial H}{\partial x_{n}}}{\Bigr \rangle }=2\langle a_{n}x_{n}^{2}\rangle \,,}$

takže střední hodnota výrazu ${\displaystyle a_{n}x_{n}^{2}}$ (tj. průměrná energie v tomto stupni volnosti) musí být rovna ${\displaystyle {\frac {1}{2}}kT}$. V některých případech dává jeden stupeň volnosti více takových příspěvků, například energie lineárního harmonického oscilátoru má kinetickou a potenciální část. Každé z nich odpovídá jeden kvadratický člen, takže celková průměrná energie je ${\displaystyle kT}$. Jindy se v hamiltoniánu vyskytuje s-tá mocnina kanonické proměnné, čemuž podle ekvipartičního teorému odpovídá průměrná energie ${\displaystyle kT/s}$ (viz příklad Sedimentace).

Předpoklady

Aby platil ekvipartiční teorém, nesmí být tepelná energie ${\displaystyle kT}$ příliš malá ve srovnání s mezerami mezi jednotlivými energetickými mikrostavy. V odvození považujeme spektrum možných energií za spojité. Při dostatečně nízké teplotě jsou některé možné pohyby výrazně méně pravděpodobné, a proto nepřispívají k celkové tepelné kapacitě tak, jak by vyplývalo z ekvipartičního teorému. Tento efekt způsobený kvantováním energie byl jedním z významných důvodů pro nahrazení klasické mechaniky kvantovou mechanikou.

Odvození ekvipartičního teorému také spoléhá na ergodickou hypotézu, tedy že v dlouhodobém průměru jsou všechny mikrostavy systému stejně pravděpodobné. K tomu je třeba, aby existoval přenos energie mezi všemi jejími formami v rámci systému.

Aplikace

Ideální plyn

Uvažme nejprve jednoatomový ideální plyn, jakým je například helium za standardních podmínek. Jeho částice se mohou volně pohybovat ve třech nezávislých směrech, nerotují, nekmitají a jejich potenciální energie je zanedbatelná. Celková energie (hamiltonián) každé částice je tedy

${\displaystyle H={\frac {1}{2}}mv^{2}={\frac {1}{2}}m\left(v_{x}^{2}+v_{y}^{2}+v_{z}^{2}\right)\,,}$

přičemž velikost rychlosti jsme vyjádřili pomocí kartézských souřadnic. V celkové energii jsou tři kvadratické příspěvky (${\displaystyle s=2}$), takže průměrná energie každé částice plynu bude ${\displaystyle {\frac {3}{2}}kT}$. Jestliže plynné těleso obsahuje ${\displaystyle N}$ částic, je vnitřní energie plynu přímo úměrná teplotě

${\displaystyle U=N\langle H\rangle ={\frac {3}{2}}NkT={\frac {3}{2}}nRT\,,}$

kde ${\displaystyle n}$ je látkové množství plynu, ${\displaystyle R=N_{\mathrm {A} }k}$ je molární plynová konstanta, ${\displaystyle N_{\mathrm {A} }}$ je Avogadrova konstanta. Protože ${\displaystyle R}$ je přibližně 2 kalorie na mol a kelvin, vyplývá z ekvipartičního teorému, že molární tepelná kapacita ideálního plynu za stálého objemu je ${\displaystyle C_{\mathrm {V} }={\frac {3}{2}}R\approx 3\,\mathrm {cal\cdot mol^{-1}\cdot K^{-1}} }$. Vzácné plyny se za běžných podmínek chovají velmi přesně jako jednoatomový ideální plyn a tato předpověď ekvipartičního teorému na nich byla experimentálně potvrzena.

Ze střední hodnoty kinetické energie lze dále určit střední kvadratickou rychlost ${\displaystyle v_{\mathrm {k} }}$.

${\displaystyle \langle E_{\mathrm {k} }\rangle ={\frac {1}{2}}m\langle v^{2}\rangle ={\frac {3}{2}}kT}$

${\displaystyle v_{\mathrm {k} }={\sqrt {\langle v^{2}\rangle }}={\sqrt {\frac {3kT}{m}}}={\sqrt {\frac {3RT}{M}}}}$

Zde je ${\displaystyle m}$ hmotnost jedné částice a ${\displaystyle M=N_{\mathrm {A} }m}$ je molární hmotnost uvažovaného plynu. Fakt, že střední kvadratická rychlost klesá s molární hmotností, byl využit mimo jiné v projektu Manhattan při obohacování uranu. Molekuly plynného UF₆, které obsahují lehčí izotop ²³⁵U, pronikají malým otvorem rychleji než těžší molekuly s izotopem ²³⁸U.

Dvouatomový plyn

Molekuly dvouatomového plynu (např. kyslíku O₂, dusíku N₂ či oxidu uhelnatého CO) si lze zjednodušeně představit jako dvě kuličky spojené pružinou. Molekula se může posouvat v prostoru jako celek, čemuž odpovídají tři stupně volnosti s kvadratickým příspěvkem k energii jako u jednoatomového plynu. Může také rotovat, ale je souměrná podle jedné osy, takže rotační stupně volnosti jsou dva, opět s kvadratickým příspěvkem (${\displaystyle J\omega ^{2}/2}$). Navíc mohou vázané atomy kmitat k sobě a od sebe, z čehož plyne jeden kvadratický příspěvek ke kinetické energii a jeden k potenciální. (Viz harmonický oscilátor níže.) Celková energie má tedy 7 kvadratických členů a ekvipartiční teorém předpovídá, že dvouatomový plyn bude mít molární kapacitu za stálého objemu

${\displaystyle C_{\mathrm {V} }={\frac {7}{2}}R\approx 7\,\mathrm {cal\cdot mol^{-1}\cdot K^{-1}} \,,}$

kde ${\displaystyle R}$ je molární plynová konstanta. Tato předpověď odpovídá skutečnosti jen při vysokých teplotách. Za běžných teplot (okolo 0 °C) molekuly nevibrují a tepelná kapacita proto klesá na ${\displaystyle 5R/2}$. Za velmi nízkých teplot „zamrzají“ i rotační stupně volnosti a tepelná kapacita dále klesá na hodnotu ${\displaystyle 3R/2}$. Například pro oxid uhelnatý je ${\displaystyle T_{\mathrm {vib} }\approx 3100\,\mathrm {K} }$ a ${\displaystyle T_{\mathrm {rot} }\approx 2{,}8\,\mathrm {K} }$. Tento nesoulad teorie s pozorováním nelze napravit žádným složitějším mechanickým modelem molekuly, protože další stupně volnosti mohou tepelnou kapacitu jedině zvýšit, nikoli snížit. V rámci klasické teorie nelze tento pokles vysvětlit, klasické zákony pohybu zde neplatí. Jev je důsledkem kvantování energie molekul a představuje jeden ze zásadních důvodů pro zavedení kvantové mechaniky.

Extrémně horký plyn

V extrémních podmínkách jako je bílý trpaslík či neutronová hvězda se částice plynu pohybují rychlostmi blízkými rychlosti světla ${\displaystyle c}$. Model jednoatomového ideálního plynu je i v těchto případech užitečný, ale zákony pohybu je třeba modifikovat podle speciální teorie relativity. Podle Pythagorovy věty o energii je při vysokých relativistických rychlostech energie částice přibližně rovna ${\displaystyle cp}$, kde ${\displaystyle p}$ je velikost hybnosti. Hamiltonián jedné částice je tedy

${\displaystyle H\approx cp=c{\sqrt {p_{x}^{2}+p_{y}^{2}+p_{z}^{2}}}\,.}$

Pro použití ekvipartičního teorému nejprve vypočítáme parciální derivace podle jednotlivých složek.

${\displaystyle p_{x}{\frac {\partial H}{\partial p_{x}}}=c{\frac {p_{x}^{2}}{\sqrt {p_{x}^{2}+p_{y}^{2}+p_{z}^{2}}}}}$

Výsledek pro složky y a z je analogický. Je zajímavé, že daný hamiltonián je roven součtu těchto tří výrazů pro každou složku.

${\displaystyle H=c{\frac {p_{x}^{2}+p_{y}^{2}+p_{z}^{2}}{\sqrt {p_{x}^{2}+p_{y}^{2}+p_{z}^{2}}}}=p_{x}{\frac {\partial H}{\partial p_{x}}}+p_{y}{\frac {\partial H}{\partial p_{y}}}+p_{z}{\frac {\partial H}{\partial p_{z}}}}$

Podle ekvipartičního teorému má každý ze sčítanců střední hodnotu ${\displaystyle kT}$, takže celkově dostáváme ${\displaystyle \langle H\rangle =3kT}$. Pro ${\displaystyle N}$ částic je celková průměrná energie ${\displaystyle U=3NkT=3nRT}$. Extrémně relativistický plyn tedy obsahuje dvojnásobek energie ve srovnání s klasickým jednoatomovým plynem.

Sedimentace

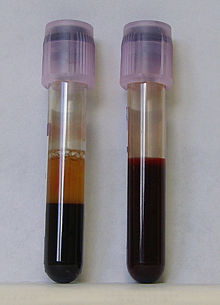
Při sedimentaci (usazování) malých částic hraje klíčovou roli potenciální energie v gravitačním poli ${\displaystyle E_{\mathrm {p} }=mgh}$, kde ${\displaystyle m}$ je hmotnost částice, ${\displaystyle g}$ je tíhové zrychlení a ${\displaystyle h}$ je souřadnice ve svislém směru (výška). Například běžný zákal v pivu může být způsoben rozptylem světla na seskupených molekulách proteinů, které vlivem tíže klesají ke dnu sklenice. Zároveň probíhá difuze vzhůru, protože shluky vykonávají Brownův pohyb. Jsou-li tyto vlivy v rovnováze, lze použít ekvipartiční teorém k odhadu výšky zákalu. Ve vztahu pro potenciální energii je první mocnina výšky, takže ${\displaystyle s=1}$ a průměrná potenciální energie bude ${\displaystyle \langle E_{\mathrm {p} }\rangle =mg\langle h\rangle =kT}$. Takže shluky proteinů o hmotnosti cca 10 MDa (zmenšeno o vliv vztlaku v kapalině) způsobí v pivu zákal vysoký v průměru asi 2 centimetry. Užitečné je, že ekvipartiční teorém lze použít pro každý stupeň volnosti zvlášť, nezávisle na ostatních. Proto jsme v tomto příkladu diskutovali pouze výšku a nemuseli jsme znát další detaily o pohybu shluků.

Harmonický oscilátor

Mnoho fyzikálních systémů vykazuje harmonické kmitání, kdy se určitá veličina v čase pravidelně mění jako funkce sinus. Může jít o mechanické oscilátory jako je pružina či kyvadlo nebo elektrický rezonanční obvod nebo dva atomy spojené chemickou vazbou a tak dále. Závaží o hmotnosti ${\displaystyle m}$ na pružině o tuhosti ${\displaystyle \kappa }$ má jednak kinetickou energii, jednak potenciální:

${\displaystyle H=E_{\mathrm {k} }+E_{\mathrm {p} }={\frac {1}{2}}{\frac {p^{2}}{m}}+{\frac {1}{2}}\kappa y^{2}\,,}$

kde ${\displaystyle p}$ je hybnost závaží a ${\displaystyle y}$ je souřadnice. Hamiltonián závisí na obou proměnných kvadraticky, takže ekvipartiční teorém říká, že kinetická i potenciální energie mají průměrnou hodnotu ${\displaystyle kT/2}$. Dohromady má oscilátor v rovnováze při teplotě ${\displaystyle T}$ energii

${\displaystyle \langle H\rangle =\langle E_{\mathrm {k} }\rangle +\langle E_{\mathrm {p} }\rangle ={\frac {1}{2}}kT+{\frac {1}{2}}kT=kT\,.}$

Tak lze kvantifikovat například tepelný šum v elektronických součástkách.

Tepelná kapacita pevné látky

Atomy v krystalické látce mohou kmitat kolem svých rovnovážných poloh ve třech nezávislých směrech. Pohyb atomu lze tedy chápat jako složení tří harmonických oscilátorů. Průměrná energie takového pohybu bude ${\displaystyle 3kT}$, takže celý krystal má vnitřní energii ${\displaystyle U=3NkT}$ a tepelnou kapacitu ${\displaystyle 3Nk=3nR}$. Molární tepelná kapacita libovolné krystalické látky by proto měla být přibližně 3R = 24,9 J/(mol·K) ≈ 6 cal/(mol·K). Tento poznatek vyjadřuje tzv. Dulongův-Petitův zákon. Například zlato má měrnou tepelnou kapacitu c = 129 J/(kg·K) a molární hmotnost M = 0,197 kg/mol, takže jeho molární tepelná kapacita je Mc = 25,4 J/(mol·K). Mírně vyšší hodnota je způsobena příspěvkem volných elektronů, protože zlato je dobrý vodič.

Ve skutečnosti ale Dulongův-Petitův zákon selhává při nízkých teplotách, zejména pro látky tvořené lehkými atomy. Například led má molární tepelnou kapacitu pouze poloviční, cca ${\displaystyle 1{,}5R}$. Selhává tedy i ekvipartiční teorém. Důvod je stejný jako u dvouatomových plynů – při nízkých teplotách jsou mezi dovolenými energiemi mezery, některé stupně volnosti proto „zamrzají“ a nepodílejí se na tepelné kapacitě. Klasický model je proto nutné nahradit kvantovým popisem. Poměrně úspěšný je Debyeův model, který popisuje interakce atomů jako výměnu fononů. Podle třetího termodynamického zákona musí molární tepelná kapacita každé látky klesat k nule při teplotách blízkých absolutní nule. Debyeův model tuto podmínku splňuje na rozdíl od jednoduché předpovědi založené na klasickém ekvipartičním teorému.

Teplota hvězdy

Pomocí ekvipartičního teorému lze odhadnout teplotu uvnitř hvězdy. Pro jednoduchost předpokládejme, že hmota hvězdy je tvořena vodíkem a má všude stejnou hustotu. U skutečných hvězd to samozřejmě neplatí, protože hustota, tlak i teplota se od povrchu do středu výrazně mění. Zároveň je zřejmé, že hvězda není ve stavu termodynamické rovnováhy, probíhá v ní řada dynamických procesů a přeměn energie. Přesto i takový jednoduchý model může dát dobrý odhad.

Celková gravitační potenciální energie při rovnoměrném rozložení hmoty ve hvězdě je

${\displaystyle E_{\mathrm {tot} }=-{\frac {3GM^{2}}{5R}}\,,}$

kde ${\displaystyle G}$ je gravitační konstanta, ${\displaystyle M}$ hmotnost hvězdy, ${\displaystyle R}$ poloměr hvězdy. Počet částic ve hvězdě lze odhadnout jako ${\displaystyle N=M/m_{\mathrm {p} }}$, kde ${\displaystyle m_{\mathrm {p} }}$ je hmotnost protonu. Průměrná potenciální energie jedné částice je tedy

${\displaystyle \langle E_{\mathrm {p} }\rangle ={\frac {E_{\mathrm {tot} }}{N}}=-{\frac {3GMm_{\mathrm {p} }}{5R}}\,.}$

Potenciální energie klesá se vzdáleností od středu jako ${\displaystyle r^{-1}}$, takže ${\displaystyle s=-1}$ a podle ekvipartičního teorému je

${\displaystyle kT=-\langle E_{\mathrm {p} }\rangle ={\frac {3GMm_{\mathrm {p} }}{5R}}\,.}$

Slunce jako typická hvězda hlavní posloupnosti má hmotnost přibližně 2×10³⁰ kg a poloměr 700 tisíc km. Užitím těchto hodnot vychází teplota 14 milionů kelvinů. Skutečná teplota v centru Slunce je 15 milionů kelvinů, takže odhad je velice přesný. Z části je to však dílem náhody, u jiných hvězd bude odhad správný jen řádově. Při takto vysokých teplotách neexistují chemické vazby, ale mohou při nich probíhat termojaderné reakce. Z ekvipartičního teorému tedy můžeme usoudit, co je zdrojem energie Slunce a hvězd.

Vznik hvězdy

Podle mlhovinové hypotézy vznikají nové hvězdy a planetární systémy z náhodně zhuštěných oblastí v zárodečné mlhovině. Nárůst hustoty může být za určitých podmínek zesílen a zpětnou vazbou způsobí zhroucení okolního plynu a prachu vlivem vlastní gravitace. Jev se nazývá Jeansova nestabilita. Dokud je oblak ve stavu stabilní rovnováhy, platí v něm ekvipartiční teorém ve tvaru

${\displaystyle 2\langle E_{\mathrm {k} }\rangle =-\langle E_{\mathrm {p} }\rangle \,.}$

(Totéž plyne z viriálového teorému.) Z toho můžeme odvodit podmínku nestability, čili podmínku pro vznik nové hvězdy. Kolaps nastane, když gravitační energie v určité části mlhoviny přesáhne dvojnásobek kinetické energie částic.

${\displaystyle {\frac {3GM^{2}}{5R}}>3NkT}$

Zde jsme využili vztah pro potenciální energii z předchozí sekce, takže pro jednoduchost předpokládáme, že hmota mlhoviny je rovnoměrně rozložena ve tvaru koule. Hmotnost tedy roste se třetí mocninou poloměru koule ${\displaystyle M={\frac {4}{3}}\pi R^{3}\varrho }$. Vyjádříme-li odtud poloměr a počet částic odhadneme opět jako ${\displaystyle N=M/m_{\mathrm {p} }}$, dostaneme po úpravě vztah pro minimální potřebnou hmotnost mlhoviny.

${\displaystyle M>{\sqrt {{\frac {3}{4\pi \varrho }}\left({\frac {5kT}{m_{\mathrm {p} }G}}\right)^{3}}}}$

Například při teplotě 150 K a hustotě 2×10⁻¹³ kg/m³ vychází zhruba 17-násobek hmotnosti Slunce, nicméně podmínky v různých mlhovinách se dost liší. Výsledky pozorování molekulárních mračen, oblastí s mladými hvězdami a zárodečnými globulemi dobře odpovídají uvedenému vztahu.

Historie

První návrhy týkající se rovnoměrného rozdělení tepelné energie v systému se datují do první poloviny 19. století a vždy souvisejí s výpočty tepelných kapacit různých látek. Skotský fyzik John James Waterston rozvíjel kinetickou teorii plynů a v roce 1843 poprvé publikoval myšlenku, že kinetická energie částic je rovnoměrně rozdělená mezi pohyby v různých směrech. Až o 16 let později pochopil další slavný Skot James Clerk Maxwell (formuloval Maxwellovy rovnice, Maxwellovo–Boltzmannovo rozdělení), že stejný díl kinetické energie připadá také na rotaci molekul. Jeho kolega Ludwig Boltzmann rozpoznal v ekvipartičním teorému vysvětlení již dříve známého Dulongova-Petitova zákona pro pevné látky, což vyžadovalo poučku zobecnit. Boltzmann předpokládal, že energie je v tepelné rovnováze rovnoměrně rozdělena mezi všechny složky pohybu.

Prakticky zároveň s úspěchy ekvipartičního teorému, už ve druhé polovině 19. století, se však objevují jeho nedostatky. Pevné látky se řídí Dulongovým-Petitovým zákonem jen při vysokých teplotách a také dvouatomové plyny při pokojové teplotě mají obvykle molární kapacitu 5 kalorií na mol a kelvin, zatímco ekvipartiční teorém předpovídá hodnotu 7. Jak poznamenal Maxwell už v roce 1875, problém je ještě mnohem hlubší, protože atomy nejsou nedělitelné, mají svou vnitřní strukturu a tím také další vnitřní stupně volnosti, které by k tepelné kapacitě měly přispívat. Další problém pro klasický ekvipartiční teorém představují kovy. Podle klasických představ obsahují kovy volné elektrony, které se chovají jako ideální plyn, takže každý elektron by měl přidávat ${\displaystyle 3kT/2}$ k tepelné energii kovu. Elektronů je v kovu hodně, ale experimenty ukazují, že jejich příspěvek k tepelné kapacitě je velice malý, řádově menší než ${\displaystyle 3R/2}$, což předpovídá ekvipartiční teorém. (Viz příklad zlata v sekci Tepelná kapacita pevné látky.)

Změnit základní a dobře experimentálně prověřené zákony pohybu a tím otřást základy celé fyziky zprvu nebylo myslitelné. Proto vědci hledali vysvětlení těchto potíží nejdříve v klasické fyzice. Například Boltzmann zastával názor, že interakce s éterem mohou způsobit, že plyny nedosáhnou tepelné rovnováhy. William Thomson, tehdy již povýšený do šlechtického stavu a známý jako Lord Kelvin, tvrdil, že když ekvipartiční teorém nesouhlasí s experimenty, musí být chyba v jeho odvození. Nedokázal ji ale konkrétně najít. Lord Rayleigh považoval odvození za správné a zároveň věřil, že tepelná rovnováha vždy nastat může, a proto požadoval nalezení nějakého nového principu, který umožní problémy obejít. Teprve Albert Einstein v roce 1906 jako první pochopil, že problém je v kvantových efektech, takže klíčem k řešení může být nová kvantová mechanika. Vytvořil vlastní model pevné látky založený na principech kvantové fyziky, ve kterém tepelná kapacita pevných látek klesá k nule s klesající teplotou, což bylo o 4 roky později experimentálně potvrzeno. Ačkoli Einsteinův model nebyl úplně přesný a byl později nahrazen Debyeovým modelem, ukázal v základních rysech správnou cestu. Společně s dalšími argumenty jako fotoefekt a tepelné záření dovedly tyto úvahy začátkem 20. století většinu fyziků k potřebě přehodnotit zákony pohybu, přejít ke kvantové teorii a postavit moderní fyziku na nových základech.