Elektronický filtr

Elektronický filtr je filtr na zpracování signálu ve formě elektrického obvodu. Tento článek popisuje filtry tvořené elektronickými součástkami se soustředěnými parametry, jejichž návrh vychází z pohledu, že filtr je tvořen bodovými prvky s určitými elektrickými vlastnostmi, které jsou propojeny krátkými dokonale vodivými spoji; tyto součástky mohou být diskrétní nebo součástí integrovaných obvodů; existují však také filtry s rozloženými parametry, které se uplatňují od vyšších kmitočtů (přes 100 MHz).
Elektronické filtry odstraňují nežádoucí frekvenční složky ze zpracovávaného signálu, zesilují požadované složky nebo obojí. Filtry lze dělit podle různých kritérií na:
- pasivní a aktivní
- analogové a digitální
- hornopropusté, dolnopropustné, pásmová propust, pásmová zádrž a all-pass
- pracující s diskrétním časem (se vzorkováním) a se spojitým časem
- lineární a nelineární
- filtry s nekonečnou impulzní odezvou (IIR typ) a filtry s konečnou impulzní odezvou (FIR typ)
Nejobvyklejšími typy elektronických filtrů jsou lineární filtry, bez ohledu na ostatní aspekty jejich návrhu. Detaily jejich návrhu a analýzy jsou popsány v článku o lineárních filtrech.
Historie
Nejstarším druhem elektronických filtrů jsou pasivní analogové lineární filtry složené pouze z rezistorů a kondenzátorů (RC-filtry) nebo rezistorů a cívek (RL-filtry). Tyto jednoduché, tak zvané jednopólové, filtry však mají velmi omezené použití. Větší kontrolu tvaru odezvy, šířky pásma a přechodového pásma poskytují mnohapólové LC filtry. Prvním z těchto filtrů byl filtr s konstantním k, který vynalezl George Ashley Campbell v roce 1910. Campbellův filtr tvoří žebříčková síť vycházející z teorie přenosového vedení. Tyto a dále vylepšené filtry, které navrhl mimo jiné Otto Zobel, se označují jako filtry s obrazem parametrů. Velký pokrok při návrhu filtrů učinil Wilhelm Cauer, který v době druhé světové války položil základy oboru syntézy obvodů. Cauerova teorie umožňuje vytvářet filtry, které přesně odpovídají určitým předepsaným frekvenčním funkcím.
Klasifikace podle technologie
Pasivní filtry
Filtry, které nevyužívají externí napájecí zdroj a neobsahují aktivní prvky, např. tranzistory, se nazývají pasivní lineární filtry. Jsou tvořeny kombinací rezistorů (R), cívek (L) a kondenzátorů (C).
Cívka brání průchodu signálu vyšších frekvencí, ale signály nižších frekvencí propouští dobře, zatímco kondenzátor se chová opačně. Filtr, v němž signál prochází cívkou nebo v němž kondenzátory propojují signálovou trasu se zemí, tlumí více signály s vyššími kmitočty a proto funguje jako dolní propust. Naopak obvod, v němž signál prochází kondenzátorem nebo je jeho signálová trasa propojena cívkou se zemí, tlumí více signály s vyššími kmitočty, a proto funguje jako horní propust. Samotné rezistory nemají vliv na potlačení určitých frekvencí, ale v obvodu s cívkami nebo kondenzátory určují časovou konstantu, která ovlivňují frekvenční odezvu obvodu.
Cívky a kondenzátory jsou reaktančními prvky filtru. Jejich počet určuje řád filtru. V tomto kontextu pokládáme laděný rezonanční LC obvod použitý v pásmové propusti nebo zádrži za jediný prvek, přestože je tvořen dvěma součástkami.
Pro vyšší kmitočty stačí menší indukčnosti a kapacity; pro kmitočty přibližně od 100 megahertzů je někdy cívka tvořena jedinou smyčkou drátu nebo proužkem plechu a kondenzátory jsou tvořen dvěma plíšky. Tyto struktury postupně přecházejí v pahýly používanými od UHF pásem výše.
Filtry s jedním reaktančním prvkem

Nejjednodušší pasivní filtry, RC a RL filtry, obsahují pouze jeden reaktanční prvek; výjimkou jsou hybridní LC filtry, které jsou tvořeny vlastní induktancí a kapacitancí jediného prvku.[1]
L-filtr
L-filtr sestává ze dvou reaktančních prvků, z nichž jeden je zapojen sériově a druhý paralelně.
T a π filtry

Tříprvkové filtry mohou mít topologii 'T' nebo 'π', které podle součástek v jednotlivých větvích mohou obě realizovat dolní propust, horní propust, pásmovou propust nebo pásmovou zádrž. Filtr může být symetrický nebo asymetrický podle požadovaných frekvenčních charakteristik. Hornopropustný T filtr na obrázku má velmi nízkou impedanci při vysokých kmitočtech, a velmi vysokou impedanci při nízkých kmitočtech. To znamená, že pokud je vložen do cesty signálu, bude propouštět vysoké kmitočty, zatímco nízké budou odraženy.
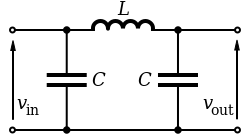
Naopak dolnopropustný π filtr na dalším obrázku při zapojení do přenosového vedení přenáší nízké kmitočty a odráží vysoké. Při použití sekcí filtrů typu m se správnými zakončovacími impedancemi bude vstupní impedance v propustném pásmu přibližně konstantní.[2]
Víceprvkové typy
Víceprvkové filtry jsou obvykle zkonstruovány jako žebříčková síť. Lze je chápat jako pokračování konstrukcí L, T a π filtrů. Pokud je třeba zlepšit některý parametr filtru např. potlačení u pásmové zádrže nebo strmost přechodu z propustného do nepropustného pásma je třeba použít víceprvkový filtr.
Aktivní filtry
Aktivní filtry jsou implementovány pomocí kombinace pasivních a aktivních (zesilovacích) komponent, a vyžadují napájecí zdroj. Při konstrukci aktivních filtrů se často se používají operační zesilovače. Aktivní filtry mohou mít vysoký činitel jakosti (Q faktor), a mohou dosáhnout rezonance bez použití cívek. Jejich horní frekvenční limit je omezen šířkou pásma operačního zesilovače.
Jiné technologie filtrů
Existuje mnoho technologií vytváření filtrů jiných než použití elektronických součástek se soustředěnými parametry – digitální filtry, krystalové filtry, mechanické filtry, filtry s povrchovou akustickou vlnou (SAW), filtry s tenkovrstvými objemovými akustickými rezonátory (TFBAR, FBAR), YIG-filtry a atomové filtry (používané v atomových hodinách).
Přenosová funkce
- Další detaily jsou ve článku Filtr (zpracování signálu)
Přenosová funkce filtru je poměr výstupního signálu k vstupnímu jako funkce komplexní frekvence :
- .
Přenosové funkce všech lineárních časově invariantních filtrů zkonstruovaných z prvků se soustředěnými parametry (na rozdíl od filtrů s rozloženými parametry např. přenosová vedení), bude poměrem dvou polynomů proměnné , tj. racionální funkce . Řád přenosové funkce bude nejvyšší mocnina , která se objevuje v čitateli nebo ve jmenovateli.
Klasifikace podle topologie
Elektronické filtry lze klasifikovat podle technologie, kterou jsou vyrobeny. Při použití technologie pasivních nebo aktivních filtrů lze filtry dále klasifikovat podle použité topologie elektronického filtru.
Libovolná daná přenosová funkce filtru může být implementována libovolnou topologií elektronického filtru.
Často se používají následující topologie:
- Cauerova topologie – pasivní
- Sallenova–Keyova topologie – aktivní
- Topologie s více zpětnými vazbami – aktivní
- Topologie se stavovou proměnnou – aktivní
- Bikvadratická topologie – aktivní
Klasifikace podle metodologie návrhu
Šablona:Lineární analogové elektronické filtry Návrh lineárních analogových filtrů historicky vznikl ze tří hlavních přístupů. Nejstarší konstrukce jsou návrhy jednoduchých obvodů, jejichž hlavním kritériem byl činitel jakosti (Q faktor) obvodu. Tento přístup vycházel z použití filtrů v rádiových přijímačích, kde činitel jakosti byl měřítkem frekvenční selektivity laděného obvodu. Od 20. let 20. století začaly být filtry navrhovány z perspektivy obrazu impedance, což byla reakce na podněty z oblasti telekomunikací. Po druhé světové válce byla dominantní metodologií syntéza obvodů. Použitá vyšší matematika si původně vyžadovala dostupnost rozsáhlých tabulek hodnot koeficientů polynomů, které byly postupně nahrazeny moderními počítačovými nástroji.[3]
Přímá obvodová analýza
Filtry nízkého řádu lze navrhovat přímým použitím základních obvodových zákonů, např. Kirchhoffových zákonů pro získání přenosové funkce. Tento druh analýzy však lze použít pouze pro jednoduché filtry 1. nebo 2. řádu.

Analýza obrazu impedance
- Podrobnější informace naleznete v článku Filtry s kompozitním obrazem.
Tento přístup analyzuje části filtru z pohledu na filtr jako na nekonečný řetěz identických částí. Jeho výhodou je jednoduchost přístupu a možnost snadného rozšíření na vyšší řády. Nevýhodou je, že přesnost predikce odezvy filtru závisí na jeho zakončeních v obrazu impedance, které obvykle nejsou známé.[4]


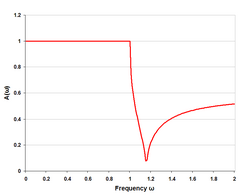

Syntéza obvodů
- Podrobnější informace naleznete v článku Network_synthesis_filters.

Návrh filtrů metodou syntézy obvodů vychází z požadované přenosové funkce, která se vyjádří jako polynomiální rovnice vstupní impedance filtru. Hodnoty součástek filtru se získají rozvojem tohoto polynomu na řetězový zlomek nebo jeho rozkladem na parciální zlomky. Na rozdíl od metody obrazu výsledný filtr nevyžaduje obvody impedančního přizpůsobení, protože zakončovací rezistory jsou obsaženy v analýze již od počátku.[4]
Na obrázcích je srovnání dolních propustí pátého řádu realizovaných jako Butterworthův filtr, dva typy Čebyševova filtru, a eliptický filtr. Konkrétní provedení, zda jde o analogový nebo digitální, pasivní nebo aktivní filtr, nezpůsobuje žádný rozdíl; jejich výstup by byl stejný.
Z obrázků je patrné, že eliptické filtry jsou ostřejší než ostatní, ale vykazují zvlnění v celé šířce pásma.
Odkazy
Reference
V tomto článku byl použit překlad textu z článku Electronic filter na anglické Wikipedii.
- ↑ Dzhankhotov.
- ↑ ARRL Handbook, 1968, s. 50.
- ↑ Bray 2002.
- ↑ a b Matthaei, Young a Jones 1964.
Literatura
- The American Radio Relay League, Inc., 1968. The ARRL Handbook, 1968. [s.l.]: [s.n.].
- BRAY, John, 2002. Innovation and the Communications Revolution: From the Victorian pioneers to broadband Internet (History and Management of Technology). [s.l.]: Institute of Electrical Engineers. Dostupné online. ISBN 978-0852962183.
- ZVEREV, Anatol I., 1969. Handbook of Filter Synthesis. [s.l.]: John Wiley & Sons. ISBN 0-471-98680-1. Katalog typů pasivních filtrů a hodnot součástek. Bible pro praktický návrh elektronických filtrů.
- Williams, Arthur B; Taylor, Fred J, 1995. Electronic Filter Design Handbook. [s.l.]: McGraw-Hill. Dostupné online. ISBN 0-07-070441-4.
- DZHANKHOTOV, Valentin, 2009. Hybrid LC filter for power electronic drives: Theory and Implementation. Lappeenranta: Lappeenranta university of technology. 112 s. Dostupné online. ISBN 978-952-214-827-8. (anglicky)
- MATTHAEI, George L.; YOUNG, Leo; JONES, E.M.T., 1964. Microwave Filters, Impedance-Matching Networks, and Coupling Structures. Norwood: McGraw-Hill. Dostupné online.
Související články
- Analogový filtr
- Audio crossover
- Audio filtr
- Kaskádovaný integrátor-hřebenový filtr
- Hřebenový filtr
- DSL filtr
- Nyquistův filtr
- VF a mikrovlnný filtr
- Filtr se spínaným kondenzátorem
- Tónová kontrola obvodů
- Napětím řízený filtr
Externí odkazy
 Obrázky, zvuky či videa k tématu filtr na Wikimedia Commons
Obrázky, zvuky či videa k tématu filtr na Wikimedia Commons  Galerie filtr na Wikimedia Commons
Galerie filtr na Wikimedia Commons- National Semiconductor AN-779 (TI SNOA224a) Katalogový list popisuje teorii analogových filtrů
- Fundamentals of Electrical Engineering and Electronics – Podrobné vysvětlení všech typů filtrů
- BAW filters (in French; PDF)
- Some Interesting Filter Design Configurations & Transformations
- Analog Filters for Data Conversion
Média použitá na této stránce
Autor: SpinningSpark ba62ca25da3fee2f8f36c101994f571c151abee7 is a SHA-1 commitment to this user's real-life identity, Licence: CC BY-SA 3.0
m-derived prototype low-pass order 5 filter response m=0.5
A circuit diagram of a simple 1st order RC lowpass filter.
Autor: Geek3, Licence: CC BY 4.0
Frequency response curves of four linear analog filters: Butterworth filter, Chebyshev filter of type 1 and 2 and Elliptic filter, each one as 5th order filter.
Autor: SpinningSpark real life identity ba62ca25da3fee2f8f36c101994f571c151abee7 SHA-1 commitment, Licence: CC BY-SA 3.0
Zobel network (constant resistance) filter. 5 sections. Scaled for comparability with other plots in w:Electronic filters article
Autor: SpinningSpark ba62ca25da3fee2f8f36c101994f571c151abee7 is a SHA-1 commitment to this user's real-life identity, Licence: CC BY-SA 3.0
m-derived prototype half-section low-pass filter response m=0.5
Autor: SpinningSpark real life identity ba62ca25da3fee2f8f36c101994f571c151abee7 SHA-1 commitment, Licence: CC BY-SA 3.0
Frequency response of composite constant k filter consisting of 4 half-sections. The scale of this plot and the number of filter elements (5) has been chosen to make the response comparable to the plots of network synthesis filters in the w:Electronic filters article.
Autor: SpinningSpark real life identity ba62ca25da3fee2f8f36c101994f571c151abee7 SHA-1 commitment, Licence: CC BY-SA 3.0
Frequency plot of RL filter prototype scaled for comparison with other plots in the w:Electronic filters article.
Autor: Arnold Reinhold, Licence: CC BY 2.5
Television signal splitter, consisting of a hi-pass and a lo-pass filter.









