Eliptická dráha

Eliptická dráha (al. eliptická orbita), v astrodynamice nebo v nebeské mechanice znamená Keplerovu dráhu s oběžnou excentricitou menší než 1 . Zahrnuje i kruhovou dráhu s excentricitou rovnou nule. V přísnějším chápání je to Keplerova dráha s excentricitou větší než 0 a menší než 1, zahrnující kruhovou dráhu. V širším smyslu je to Keplerova dráha s negativní energií. Ta zahrnuje radiální eliptickou oběžnou dráhu s excentricitou rovnající se 1.

V gravitačním problému dvou těles s negativní energií, obě tělesa se pohybují po eliptické oběžné dráze se stejnou délkou doby oběhu kolem společného barycentra. Také relativní pozice jednoho tělesa s ohledem na druhé se pohybuje po eliptické oběžné dráze.

Mezi eliptické oběžné dráhy patří i dvojeliptická přechodová dráha, Hohmannova přechodová dráha, a zvláštním případem vysoké eliptické dráhy jsou dráha typu Molnija a sněžní dráha. Mezi Eliptické dráhy patří i setrvačná fáze suborbitálního letu, která probíhá po eliptické dráze, ale na rozdíl od klasických eliptických drah protíná povrch míjení tělesa.

Rychlost

Při standardním předpokladu kruhová rychlost (${\displaystyle v\,}$), tělesa pohybujícího se po eliptické dráze, může být vypočtena jako:

${\displaystyle v={\sqrt {\mu \left({2 \over {r}}-{1 \over {a}}\right)}}}$

Kde:

• ${\displaystyle \mu \,}$ Je standardní gravitační parametr,
• ${\displaystyle r\,}$ Je vzdálenost mezi obíhajícími tělesy,
• ${\displaystyle a\,\!}$ Je délka střední poloosy.

Rovnice rychlosti pro hyperbolickou trajektorii má navíc + ${\displaystyle {1 \over {a}}}$, nebo je stejná, ale v tom případě je záporná.

Oběžná doba

Při standardním předpokladu doby oběhu (${\displaystyle P\,\!}$), tělesa pohybujícího se po eliptické dráze, může být vypočtena jako:

${\displaystyle P=2\pi {\sqrt {a^{3} \over {\mu }}}}$

Kde:

• ${\displaystyle \mu \,}$ Je standardní gravitační parametr,
• ${\displaystyle a\,\!}$ Je délka střední poloosy.

Výsledek:

• Doba oběhu je podobná té při kruhové dráze s oběžným poloměrem podobným střední poloosy (${\displaystyle a\,\!}$).
• Pro danou střední poloosa oběžná doba nezávisí na Excentric (viz také třetí Keplerův zákon).

Energie

Při standardním předpokladu specifická oběžná energie (${\displaystyle \epsilon \,}$), eliptické dráhy je záporná a oběžná energie zachování rovnosti pro danou oběžnou dráhu může být:

${\displaystyle {v^{2} \over {2}}-{\mu \over {r}}=-{\mu \over {2a}}=\epsilon <0}$

Kde:

• ${\displaystyle v\,}$ Je kruhová rychlost obíhajícího tělesa,
• ${\displaystyle r\,}$ Je vzdálenost obíhajícího tělesa od centrálního tělesa,
• ${\displaystyle a\,}$ Je délka střední poloosy,
• ${\displaystyle \mu \,}$ Je standardní gravitační parametr.

Výsledek:

• Pro danou střední poloosa, specifická oběžná energie je nezávislá od excentricity.

Použitím virové teorie zjistíme:

• Průměrný čas specifické potenciální energie je rovný 2ε,
  • Průměrný čas r⁻¹ je a⁻¹
• Průměrný čas specifické kinetické energie je rovný-ε,

Úhel dráhy pohybu

${\displaystyle h\,=r\,v\,\cos \phi }$

Kde:

• ${\displaystyle h\,}$ Je specifický relativní moment hybnosti oběžné dráhy,
• ${\displaystyle v\,}$ Je kruhová rychlost obíhajícího tělesa,
• ${\displaystyle r\,}$ Je radiální vzdálenost obíhajícího tělesa od centrálního tělesa,
• ${\displaystyle \phi \,}$ Je úhel dráhy pohybu.

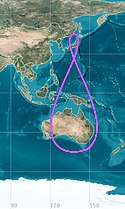
Průmět dráhy na centrální těleso

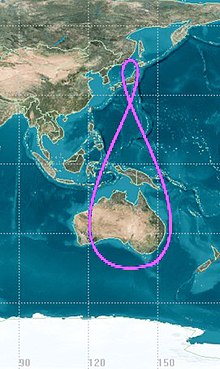
Průmět oběžné dráhy je složen z pohybu obíhajícího tělesa a z vlastní rotace míjení tělesa.

Kolmý průmět eliptické dráhy na obíhané těleso má nejčastěji tyto tvary:

• Bod - geostacionární dráha s malou excentricitou
• Úsečka - eliptická synchronní dráha se sklonem 0 °
• Přímka - rovníková dráha, se sklonem 0 °
• Sinusoida - eliptické dráhy, se sklonem k rovníku a s malou excentricitou - typická pro běžné satelity s kruhovou ORBITAL
• Cykloidní- vysoké eliptické dráhy, se sklonem k rovníku cca 63 ° -116 ° a s excentrickou dráhou, s periodou pod 24hodin - typ Molnija
• Osmičková - vysoké eliptické dráhy, se sklonem k rovníku cca 63 ° -116 ° as velkou excentricitou, s periodou 1den - typ Tundra

Reference

V tomto článku byl použit překlad textu z článku Eliptická dráha na slovenské Wikipedii.

Literatura

• D’ELISEO, MM. The first-order orbital equation. American Journal of Physics. 2007, s. 352 – 355. DOI 10.1119/1.2432126. (anglicky) Je zde použita šablona {{Cite journal}} označená jako k „pouze dočasnému použití“.
• D’ELISEO, MM. The gravitational ellipse. Journal of Mathematical Physics. 2009, s. 022901-022901-10 doi = 10.1063/1.3078419. (anglicky) Je zde použita šablona {{Cite journal}} označená jako k „pouze dočasnému použití“.

Související články

• Dvojeliptická přechodová dráha
• Hohmannova přechodová dráha
• Hyperbolické trajektorie
• Keplerova dráha
• Kruhová dráha
• Vysoká eliptická dráha

Externí odkazy

• Základy kosmických letů ⇒ orbitální mechanika
• Měsíční fotografické porovnání
• Afélium - Perihelion
• Tundra_Orbits.wmv