Funktor

Funktor je pojem z matematiky, konkrétněji z teorie kategorií. Jde o zobecnění pojmu zobrazení. Funktor přiřazuje objektům nějaké kategorie objekty jiné kategorie a morfismům kategorie morfismy jiné kategorie.

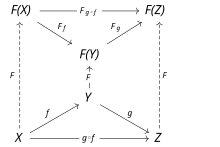
Pro kategorie C a D je funktor F z C do D zobrazení,^[1] které

• přiřadí každému objektu ${\displaystyle X\in C}$ objekt ${\displaystyle F(X)\in D}$,
• přiřadí každému morfismu ${\displaystyle f:X\rightarrow Y\in C}$ morfismus ${\displaystyle F(f):F(X)\rightarrow F(Y)\in D}$, tak, že je splněno
  • ${\displaystyle F(\mathrm {id} _{X})=\mathrm {id} _{F(X)}}$ pro každý objekt ${\displaystyle X\in C}$
  • ${\displaystyle F(g\circ f)=F(g)\circ F(f)}$ pro všechny morfismy ${\displaystyle f:X\rightarrow Y}$ a ${\displaystyle g:Y\rightarrow Z}$.

Tj. funktory musí zachovávat identické morfismy a skládání morfismů.

V matematice existuje mnoho konstrukcí, které se chovají funktory, ale „obracejí morfismy“ a „přehazují pořadí skládání“. Proto definujeme kontravariantní funktor F z C do D jako zobrazení, které

• přiřadí každému objektu ${\displaystyle X\in C}$ objekt ${\displaystyle F(X)\in D}$,
• přiřazuje každému morfismus ${\displaystyle f\colon X\to Y\in C}$ morfismus ${\displaystyle F(f)\colon F(Y)\to F(X)\in D}$ takový, že platí následující dvě podmínky:
  • ${\displaystyle F(\mathrm {id} _{X})=\mathrm {id} _{F(X)}\,\!}$ pro každý objekt ${\displaystyle X\in C}$,
  • ${\displaystyle F(g\circ f)=F(f)\circ F(g)}$ pro všechny morfismy ${\displaystyle f\colon X\to Y}$ a ${\displaystyle g\colon Y\to Z\in C}$.

Variance (složeného) funktoru^[2]

• Složení dvou funktorů stejné variance:
  • ${\displaystyle \mathrm {Covariant} \circ \mathrm {Covariant} \to \mathrm {Covariant} }$
  • ${\displaystyle \mathrm {Contravariant} \circ \mathrm {Contravariant} \to \mathrm {Covariant} }$
• Složení dvou funktorů opačné variance:
  • ${\displaystyle \mathrm {Covariant} \circ \mathrm {Contravariant} \to \mathrm {Contravariant} }$

Všimněte si, že kontravariantní funktory obracejí směr skládání.

Obyčejné funktory se také nazývají kovariantní funktory pro rozlišení od kontravariantních funktorů. Všimněte si, že kontravariantní funktor je možné definovat jako kovariantní funktor na opačné kategorii ${\displaystyle C^{\mathrm {op} }}$.^[3] Někteří autoři preferují psaní všech výrazů kovariantně. To znamená, že neříkají, že ${\displaystyle F\colon C\to D}$ je kontravariantní funktor, ale ${\displaystyle F\colon C^{\mathrm {op} }\to D}$ (nebo někdy ${\displaystyle F\colon C\to D^{\mathrm {op} }}$) a ${\displaystyle F}$ nazývají funktorem.

Kontravariantní funktory se někdy také nazývají kofunktory.^[4]

Výše uvedená definice je definice kovariantního funktoru. Kontravariantní funktor je takové zobrazení F, které morfismu ${\displaystyle f:X\to Y}$ kategorie C přiřadí morfismus ${\displaystyle F(f):F(Y)\to F(X)}$ v kategorii D a platí ${\displaystyle F(f\circ g)=F(g)\circ F(f)}$.

V tomto článku byl použit překlad textu z článku Functor na anglické Wikipedii.

• JACOBSON, Nathan, 2009. Basic Algebra I. 2. vyd. [s.l.]: Dover Publications. 499 s. Dostupné online. ISBN 978-0-486-47187-7. (anglicky) 
• POPESCU, Nicolae; POPESCU, Liliana, 1979. Theory of categories. Dordrecht: Springer. Dostupné online. ISBN 9789400995505. 
• SIMMONS, Harold, 2011. An Introduction to Category Theory. [s.l.]: [s.n.]. Dostupné online. ISBN 978-1-107-01087-1. DOI 10.1017/CBO9780511863226.004. Kapitola Functors and natural transformations, s. 72–107. 

• Anafunktor
• Profunktor
• Kategorie funktorů
• Kanovo rozšíření
• Pseudofunktor

• Obrázky, zvuky či videa k tématu funktor na Wikimedia Commons
• Functor [online]. Springer [cit. 2024-09-25]. Dostupné online. p/f042140. 
• nLab [cit. 2024-09-25]. Dostupné online. 
• André Joyal, CatLab, Wiki projekt pro prezentaci teorie kategorií
• HILLMAN, Chris, 2001. A Categorical Primer [online]. 2001. Dostupné v archivu pořízeném z originálu dne 1997-05-03. 
• ADÁMEK, Jiří; HERRLICH, Horst; STRECKER, George E., 2004. Abstract and Concrete Categories; The Joy of Cats [online]. 2004 [cit. 2020-09-19]. Dostupné v archivu pořízeném z originálu dne 2015-04-21. 
• Stanford Encyclopedia of Philosophy: “Category Theory“ – autor Jean-Pierre Marquis. Rozsáhlá bibliografie.
• Seznam konferencí o teorii kategorií
• Baez, John, 1996,“The Tale of n-categories.“ Neformální úvod do kategorií vyššího řádu.
• WildCats – balíček pro systém Mathematica věnovaný teorii kategorií. Manipulace a vizualizace objektů, morfismy, kategorie, funktory, přirozené transformace, univerzální vlastnosti.
• The catsters, YouTube kanál o teorii kategorií.
• Video archive záznamy hovorů o kategoriích, logice a základech fyziky.
• Interaktivní stránka, která generuje příklady kategorických konstrukcí v kategorii konečných množin.