Fibrovaný prostor

Pod pojmem fibrovaný prostor se v matematice, zejména pak v topologii, rozumí objekt, jenž je v jistém smyslu zobecněním pojmu kartézského součinu množin. Jedná se o prostor, který lze lokálně popsat jako kartézský součin, globálně však může mít netriviální topologickou strukturu. Známými příklady jednoduchých netriviálních fibrovaných prostorů jsou například Möbiova páska či Kleinova láhev. Aplikace tento topologický pojem nachází v různých odvětvích fyziky, kde lze s jeho pomocí např. konzistentně popisovat polohy a hybnosti fyzikálních systémů v klasické mechanice, pole v kvantové teorii pole či vlastnosti časoprostoru v obecné teorii relativity. Kalibrační teorie pak nacházejí v teorii fibrovaných prostorů solidní matematický základ.

Definice

Zde si představíme definici fibrovaného prostoru, jež může působit dost abstraktním a těžko stravitelným dojmem. V následujícím oddíle je proto tento pojem vyložen v povědomějších termínech pro snazší pochopení. Navíc, v následující definici požadujeme, aby jednotlivé množiny byly diferencovatelné variety. Tento požadavek však není nutný a místo diferencovatelných variet lze brát obecněji topologické prostory, kde současně místo hladkosti zobrazení vystupujících v definici požadujeme pouze jejich spojitost. Fibrované prostory, kde za množiny bereme diferencovatelné variety, se pak v tomto kontextu označují jako diferencovatelné fibrované prostory.

Fibrovaný prostor

Fibrovaný prostor (angl. fibre bundle) je definován jako uspořádaná čtveřice ${\displaystyle \scriptstyle (E,M,F,\pi )}$ následujících objektů:

1. ${\displaystyle E}$ je diferencovatelná varieta zvaná totální prostor,
2. ${\displaystyle M}$ je diferencovatelná varieta zvaná bázová varieta či báze,
3. ${\displaystyle F}$ je diferencovatelná varieta zvaná typické vlákno, nebo jen vlákno,
4. ${\displaystyle \pi :E\to M}$ je surjektivní zobrazení totálního prostoru na bázovou varietu, který se nazývá projekce.
5. Spolu s předchozími objekty je nutno zadat i otevřené pokrytí ${\displaystyle \scriptstyle \{U_{\alpha }\}_{\alpha \in I}}$ bázové variety ${\displaystyle \scriptstyle M}$ a jemu odpovídající množinu zobrazení ${\displaystyle \scriptstyle \{\varphi _{\alpha }\}_{\alpha \in I}}$, kde index ${\displaystyle \scriptstyle \alpha }$ probíhá (ne nutně konečnou či spočetnou) indexovou množinu ${\displaystyle \scriptstyle I}$. Platí tedy ${\displaystyle \scriptstyle \bigcup _{\alpha \in I}U_{\alpha }=M}$, kde ${\displaystyle \scriptstyle U_{\alpha }}$ jsou otevřené množiny. Dále, pro každé ${\displaystyle \scriptstyle \alpha }$ je zobrazení ${\displaystyle \scriptstyle \varphi _{\alpha }:U_{\alpha }\times F\to \pi ^{(-1)}(U_{\alpha })}$ difeomorfizmus splňující dodatečnou podmínku

${\displaystyle \pi (\varphi _{\alpha }(m,f))=m,\quad \forall m\in M}$,

kde symbolem ${\displaystyle \scriptstyle \pi ^{(-1)}(U_{\alpha })}$ značíme vzor množiny ${\displaystyle \scriptstyle U_{\alpha }}$ při zobrazení ${\displaystyle \scriptstyle \pi }$. Zobrazení ${\displaystyle \scriptstyle \varphi _{\alpha }}$ se nazývají lokální trivializace. (Někdy se za lokální trivializace berou zobrazení ${\displaystyle \scriptstyle {\tilde {\varphi }}_{\alpha }:\pi ^{(-1)}(U_{\alpha })\to U_{\alpha }\times F}$, která v podstatě odpovídají inverzím pro námi zavedené trivializace ${\displaystyle \scriptstyle \varphi _{\alpha }}$. Neboť jsou lokální trivializace bijekce, tak vztah zobrazení a jeho inverze je jednoznačný a oba přístupy jsou tak ekvivalentní.)

Fibrovaný prostor ${\displaystyle \scriptstyle (E,M,F,\pi )}$ se často značí jen jako ${\displaystyle \scriptstyle E}$ nebo výrazem

${\displaystyle E\ {\stackrel {\pi }{\rightarrow }}\ M}$.

Přísně vzato, definice fibrovaného prostoru by měla být nezávislá na konkrétní volbě otevřeného pokrytí ${\displaystyle \scriptstyle \{U_{\alpha }\}_{\alpha }}$. Matematicky korektně se tedy postupuje tak, že se nejdříve definicí výše zavádějí souřadnicové fibrované prostory ^{[pozn. 1]} ${\displaystyle \scriptstyle (E,M,F,\pi ,\{U_{\alpha }\}_{\alpha \in I},\{\varphi _{\alpha }\}_{\alpha \in I})}$. Na množině všech takovýchto souřadnicových fibrovaných prostorů s různými pokrytími se zadefinuje relace ekvivalence tak, že ${\displaystyle \scriptstyle (E,M,F,\pi ,\{U_{\alpha }\}_{\alpha \in I},\{\varphi _{\alpha }\}_{\alpha \in I})}$ je ekvivalentní s ${\displaystyle \scriptstyle (E,M,F,\pi ,\{V_{\beta }\}_{\beta \in J},\{\varphi _{\beta }\}_{\beta \in J})}$ právě tehdy, když ${\displaystyle \scriptstyle (E,M,F,\pi ,\{U_{\alpha }\}_{\alpha \in I}\cup \{V_{\beta }\}_{\beta \in J},\{\varphi _{\alpha }\}_{\alpha \in I}\cup \{\varphi _{\beta }\}_{\beta \in J})}$ je opět souřadnicovým fibrovaným prostorem. Množinu všech souřadnicových fibrovaných prostorů si tedy můžeme faktorizovat podle této ekvivalence a fibrovaný prostor samotný je pak definován jako třída ekvivalence v tomto faktorprostoru. ^[1]

Přechodová zobrazení

Okolí ${\displaystyle \scriptstyle \{U_{\alpha }\}_{\alpha }}$ pokrývají bázovou varietu ${\displaystyle \scriptstyle M}$. Ke každému ${\displaystyle \scriptstyle U_{\alpha }}$ je přitom přiřazena lokální trivializace ${\displaystyle \scriptstyle \varphi _{\alpha }}$. Na průniku dvou okolí ${\displaystyle \scriptstyle U_{\alpha }\cap U_{\beta }}$ tak máme bod ${\displaystyle \scriptstyle p\in E}$ totálního prostoru vyjádřen pomocí dvou různých trivializací

${\displaystyle p=\varphi _{\alpha }(m,f_{\alpha })=\varphi _{\beta }(m,f_{\beta }),}$

kde ${\displaystyle \scriptstyle m\in M}$ je takové, že platí ${\displaystyle \scriptstyle \pi (p)=m}$. Skutečnost, že v obou případech máme stejné ${\displaystyle \scriptstyle m\in M}$ pro obě trivializace vyplývá z požadavku kladeného na tato zobrazení v definici fibrovaného prostoru. Co je obecně různé jsou však prvky ${\displaystyle \scriptstyle f_{\alpha },f_{\beta }\in F}$. Můžeme si tak zavést zobrazení ${\displaystyle \scriptstyle \tau _{\alpha \beta }^{(m)}:F\to F}$ předpisem

${\displaystyle \tau _{\alpha \beta }^{(m)}(f_{\alpha })=f_{\beta }}$.

Takto zavedeným zobrazením se říká přechodové funkce. Konvence pro jejich značení se liší u různých autorů. Místo označení ${\displaystyle \scriptstyle \tau _{\alpha \beta }}$ se tak lze setkat i s opačným pořadím indexů ${\displaystyle \scriptstyle \tau _{\beta \alpha }}$ apod. Přechodové funkce se mají k lokálním trivializacím způsobem

${\displaystyle (\varphi _{\beta }^{-1}\circ \varphi _{\alpha })(m,f)=(m,\tau _{\alpha \beta }^{(m)}f),\quad \forall m\in M,\ \forall f\in F}$.

Pokud ${\displaystyle \scriptstyle \alpha =\beta }$, je odpovídající přechodová funkce ${\displaystyle \scriptstyle \tau _{\alpha \alpha }}$ zjevně rovna identitě. Dále, pokud platí ${\displaystyle \scriptstyle \tau _{\alpha \beta }(f_{\alpha })=f_{\beta }}$, tak zřejmě i ${\displaystyle \scriptstyle \tau _{\beta \alpha }(f_{\beta })=f_{\alpha }}$, z čehož vyplývá ${\displaystyle \scriptstyle \tau _{\alpha \beta }^{-1}=\tau _{\beta \alpha }}$. Pokud bychom neuvažovali pouze body z průniku dvou okolí ${\displaystyle \scriptstyle U_{\alpha }\cap U_{\beta }\subset M}$, ale rovnou ze tří okolí ${\displaystyle \scriptstyle U_{\alpha }\cap U_{\beta }\cap U_{\gamma }\subset M}$, tak bychom podobnými úvahami dospěli i ke vztahu

${\displaystyle \tau _{\alpha \gamma }=\tau _{\beta \gamma }\circ \tau _{\alpha \beta }}$.

Ukázali jsme tak, že v množině všech přechodových zobrazení ${\displaystyle \scriptstyle \{\tau _{\alpha \beta }\}_{\alpha ,\beta }}$ se nachází jednotkový prvek (identické zobrazení), každý prvek má k sobě inverzní prvek a že tato množina je uzavřená vůči operaci skládání prvků coby zobrazení. Skládání zobrazení je asociativní a tyto všechny vlastnosti nám tedy říkají, že množina všech přechodových zobrazení (spolu s operací skládání zobrazení) tvoří grupu. Této grupě se říká strukturní grupa. V našem postupu jsme měli zadány lokální trivializace a z nich jsme sestrojili přechodové funkce. Lze se však vydat i opačným směrem, kdy máme předem zadané přechodové funkce a z nich jsme schopni zrekonstruovat lokální trivializace, viz oddíl Rekonstrukce fibrovaného prostoru ze znalosti přechodových zobrazení níže. Strukturní grupa se tedy někdy vyskytuje v samotné definici fibrovaného prostoru.

Související pojmy

• Vzor jednobodové množiny ${\displaystyle \scriptstyle \{m\}}$ při zobrazení ${\displaystyle \scriptstyle \pi }$, tj. ${\displaystyle \scriptstyle \pi ^{(-1)}(\{m\})\subset E}$ pro daný bod ${\displaystyle \scriptstyle m\in M}$ bázové variety, nazýváme vlákno nad bodem m. Množina ${\displaystyle \scriptstyle \pi ^{(-1)}(\{m\})}$ je diferencovatelná varieta izomorfní typickému vláknu ${\displaystyle \scriptstyle F}$.

• Jako řez, resp. řez fibrovaného prostoru, označujeme hladké zobrazení ${\displaystyle \scriptstyle \sigma :M\to E}$ vyhovující podmínce ${\displaystyle \scriptstyle \pi \circ \sigma =\mathrm {Id} }$, kde ${\displaystyle \scriptstyle \mathrm {Id} }$ označuje identitu na bázové varietě. Právě uvedenou podmínku lze přepsat do tvaru

${\displaystyle \pi (\sigma (m))=m,\quad \forall m\in M}$.

Množina všech řezů na prostoru ${\displaystyle \scriptstyle E}$ se často značí symbolem ${\displaystyle \scriptstyle \Gamma (E)}$. Podobně, jako lokální řez (na okolí ${\displaystyle \scriptstyle U}$) označíme hladké zobrazení ${\displaystyle \scriptstyle \sigma :U\to E}$ vyhovující podmínce ${\displaystyle \scriptstyle \pi \circ \sigma =\mathrm {Id} |_{U}}$, kde ${\displaystyle \scriptstyle U\subset M}$ je otevřená podmnožina bázové variety. Důvod, proč se řezy nazývají právě „řezy“, je ten, že zobrazení ${\displaystyle \scriptstyle \sigma }$ vybere pro daný bod ${\displaystyle \scriptstyle m\in M}$ bázové variety jen jeden bod ${\displaystyle \scriptstyle p\in E}$ z vlákna nad bodem ${\displaystyle \scriptstyle m}$. Pro libovolné další ${\displaystyle \scriptstyle m'\in M}$ se už nemůže stát, že by ${\displaystyle \scriptstyle \sigma (m')}$ spadlo do téhož vlákna. Situace je lépe nahlédnutelná na animovaném Obr. 2 níže. V tomto případě je řezem hladké zobrazení ${\displaystyle \scriptstyle \sigma }$, které bere body kružnice a vrací body v Möbiově pásce. Na obrázku je v Möbiově pásce vyznačen větší počet typických vláken, v tomto případě představovaných úsečkami. Celá úsečka přitom odpovídá jedinému bodu kružnice. Řez ${\displaystyle \scriptstyle \sigma }$ bere po řadě body kružnice a každému takovému bodu přiřazuje jen jeden bod na odpovídající úsečce.

• Zobrazením fibrovaných prostorů ${\displaystyle \scriptstyle (E,M,F,\pi )}$ a ${\displaystyle \scriptstyle (E',M',F',\pi ')}$ nazýváme dvojici zobrazení ${\displaystyle \scriptstyle \phi :E\to E'}$ a ${\displaystyle \scriptstyle \psi :M\to M'}$ splňující podmínku

${\displaystyle \pi '\circ \phi =\psi \circ \pi }$.

• Mějme fibrovaný prostor ${\displaystyle \scriptstyle (E,M,F,\pi )}$. Pokud existuje vzájemně jednoznačné zobrazení fibrovaných prostorů ${\displaystyle \scriptstyle (E,M,F,\pi )}$ a ${\displaystyle \scriptstyle (M\times F,M,F,\pi ')}$, (kde ${\displaystyle \scriptstyle \pi '((m,f))=m}$) tak říkáme, že fibrovaný prostor ${\displaystyle \scriptstyle (E,M,F,\pi )}$ je triviální. Tehdy je ${\displaystyle \scriptstyle (E,M,F,\pi )}$ v podstatě pouze kartézským součinem ${\displaystyle \scriptstyle M\times F}$.

• Dva fibrované prostory ${\displaystyle \scriptstyle (E,M,F,\pi )}$ a ${\displaystyle \scriptstyle (E',M',F',\pi ')}$ jsou ekvivalentní, existuje-li zobrazení fibrovaných prostorů ${\displaystyle \scriptstyle (\phi ,\psi )}$ tak, že ${\displaystyle \scriptstyle \psi :M\to M'}$ je identické zobrazení a ${\displaystyle \scriptstyle \phi :E\to E'}$ je difeomorfizmus.

Grafická interpretace

Kartézský součin

Jak již bylo řečeno, fibrovaný prostor má do jisté míry zobecňovat pojem kartézského součinu. Popravdě řečeno, kartézský součin dvou diferencovatelných variet ${\displaystyle \scriptstyle A\times B}$ lze chápat jako jednoduchý fibrovaný prostor ${\displaystyle \scriptstyle (A\times B,B,A,\pi )}$, kde ${\displaystyle \scriptstyle A\times B}$ je nyní totální prostor, ${\displaystyle \scriptstyle B}$ je bázová varieta a ${\displaystyle \scriptstyle A}$ je typické vlákno. Projekci ${\displaystyle \scriptstyle \pi }$ si v tomto případě můžeme definovat způsobem ${\displaystyle \scriptstyle \pi ((a,b))=b}$, pro libovolné ${\displaystyle \scriptstyle a\in A}$, ${\displaystyle \scriptstyle b\in B}$. Pokud si dále vezmeme nějaké otevřené pokrytí ${\displaystyle \scriptstyle \{U_{\alpha }\}_{\alpha }}$ variety ${\displaystyle \scriptstyle B}$, tak ke každému okolí ${\displaystyle \scriptstyle U_{\alpha }}$ můžeme definovat lokální trivializaci ${\displaystyle \scriptstyle \varphi _{\alpha }(a,b)=(a,b)}$, která ze dvou bodů vytvoří jejich uspořádanou dvojici. Máme tak všechny suroviny vystupující v definici fibrovaného prostoru a můžeme uzavřít, že kartézský součin je skutečně triviálním případem fibrovaného prostoru.

Nezůstaňme ovšem jen u triviálních případů. Každý fibrovaný prostor, resp. jeho totální prostor, totiž jako kartézský součin vypadá alespoň lokálně. Zhruba řečeno je ke každému bodu bázové variety ${\displaystyle \scriptstyle M}$ přilepena jiná varieta, vlákno ${\displaystyle \scriptstyle F}$. Ostatně samotné lokální trivializace ${\displaystyle \scriptstyle \varphi _{\alpha }}$, jak již jejich název dává tušit, slouží k lokálnímu převodu totálního prostoru na kartézský součin dvou množin. Pro každé okolí ${\displaystyle \scriptstyle U_{\alpha }}$ lze množinu ${\displaystyle \scriptstyle V_{\alpha }=\pi ^{(-1)}(U_{\alpha })}$ (která je podmnožinou totálního prostoru ${\displaystyle \scriptstyle E}$) zobrazit díky ${\displaystyle \scriptstyle \varphi _{\alpha }^{-1}}$ difeomorfně na kartézský součin okolí a vlákna, tj.

${\displaystyle \varphi _{\alpha }^{-1}:V_{\alpha }\to U_{\alpha }\times F}$.

Möbiova páska

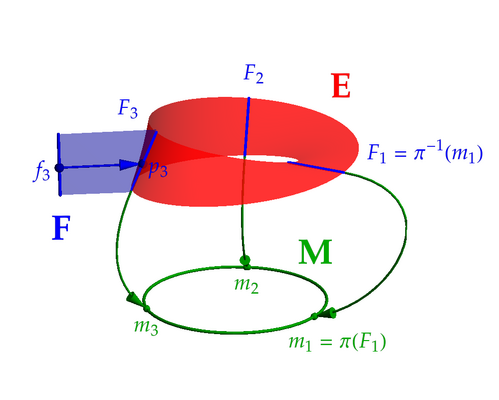
Jedním z nejjednodušších příkladů fibrovaných prostorů, které nelze vyjádřit jako kartézský součin, je Möbiova páska, na níž lze pěkně ilustrovat role jednotlivých objektů vystupujících v definici fibrovaného prostoru. Celá situace je znázorněna na obr. 1 níže. Na tomto obrázku vidíme následující:

1. červenou barvou je vyobrazen totální prostor E, tedy v tomto případě Möbiova páska,
2. zelenou barvou je vykreslena bázová varieta M, která je v našem případě obyčejnou kružnicí,
3. modrou barvou je zachyceno typické vlákno F; v našem případě se jedná o úsečku.

Na bázové varietě, kružnici, jsou dále pro názornost vybrány tři různé body ${\displaystyle \scriptstyle m_{1},m_{2},m_{3}}$. Vzory těchto bodů při projekci ${\displaystyle \scriptstyle \pi }$ jsou po řadě vlákna ${\displaystyle \scriptstyle F_{1},F_{2},F_{3}}$. Vlákno nad bodem ${\displaystyle \scriptstyle m_{1}}$ je tedy označeno ${\displaystyle \scriptstyle F_{1}}$ a podobně pro ostatní body. Vidíme tak, že jednomu bodu kružnice odpovídá celá úsečka bodů na Möbiově pásce. Každá z těchto úseček je v podstatě rovna typickému vláknu ${\displaystyle \scriptstyle F}$. Jednotlivé body na dané úsečce lze pak rozlišit pomocí bodů z typického vlákna, kterážto situace je znázorněna pro případ bodu ${\displaystyle \scriptstyle p_{3}\in E}$. Jeho projekce na bázovou varietu je ${\displaystyle \scriptstyle m_{3}}$ a v rámci vlákna ${\displaystyle \scriptstyle F_{3}}$ je ${\displaystyle \scriptstyle p_{3}}$ jednoznačně identifikován bodem ${\displaystyle \scriptstyle f_{3}\in F}$. Nějakému jinému prvku ${\displaystyle \scriptstyle p_{4}}$ ze stejného vlákna ${\displaystyle \scriptstyle F_{3}}$ by odpovídal jiný bod ${\displaystyle \scriptstyle f_{4}\in F_{3}}$, ačkoli jeho projekce ${\displaystyle \scriptstyle \pi (p_{4})}$ by byla stále rovna ${\displaystyle \scriptstyle m_{3}\in M}$, tj. ${\displaystyle \scriptstyle \pi (p_{4})=m_{3}}$.

• 

  Obr. 1: Möbiova páska coby fibrovaný prostor. Möbiova páska samotná představuje totální prostor E. Bázovou varietou M je kružnice a typickým vláknem F je úsečka. Explicitně jsou vyobrazeny tři body na kružnici a jim odpovídající vlákna na Möbiově pásce. Bod ${\displaystyle \scriptstyle p_{3}}$ na pásce je parametrizován jednak svou projekcí ${\displaystyle \scriptstyle m_{3}}$, jednak prvkem vlákna ${\displaystyle \scriptstyle f_{3}}$.

• 

  Obr. 2: Möbiovu pásku lze obdržet jako kružnici, po níž přecházíme úsečkou, kterou postupně stáčíme aby při oběhnutí kružnice hladce nasedla na svou původní, výchozí, polohu. V animaci jsou zobrazena modrou barvou vlákna nad některými body kružnice.

Báze, vlákno a projekce

Způsob, jakým se došlo od Möbiově pásce ke kružnici, coby bázové varietě, s úsečkou, coby vláknem, je naznačen v animaci na Obr. 2 a podrobněji matematicky rozebrán v následujícím. Möbiova páska je dvourozměrná varieta, kterou můžeme vložit do trojrozměrného prostoru ${\displaystyle \scriptstyle \mathbb {R} ^{3}}$ a na jejíž body se pak díky tomu můžeme odkazovat pomocí jejich souřadnic ${\displaystyle \scriptstyle (x,y,z)}$. Parametrické rovnice Möbiovy křivky o jednotkovém poloměru a jednotkové šířce v těchto souřadnicích potom znějí

${\displaystyle {\begin{array}{rcl}x(u,v)&=&(1+u\cos({\frac {v}{2}}))\cos(v),\\y(u,v)&=&(1+u\cos({\frac {v}{2}}))\sin(v),\\z(u,v)&=&u\,\sin({\frac {v}{2}}),\end{array}}}$

kde ${\displaystyle \scriptstyle u\in [-1/2,1/2]}$ a ${\displaystyle \scriptstyle v\in [0,2\pi )}$. Od teď nebudeme rozlišovat mezi Möbiovou páskou a jejím vložením do ${\displaystyle \scriptstyle \mathbb {R} ^{3}}$. Pod bodem Möbiovy pásky tak budeme rozumět trojici čísel ${\displaystyle \scriptstyle (x,y,z)}$ vyhovující parametrickým rovnicím výše.

Položíme-li ${\displaystyle \scriptstyle u=0}$ pevně, tak okamžitě vidíme, že křivka ${\displaystyle \scriptstyle \{(x(0,v),y(0,v),z(0,v))|v\in [0,2\pi )\}}$ je jednotková kružnice ležící ve vodorovné rovině, neboť platí

${\displaystyle (x(0,v))^{2}+(y(0,v))^{2}=1,\quad z(0,v)=0,\quad \forall v\in [0,2\pi )}$.

Za bázovou varietu si tedy skutečně můžeme vzít jednotkovou kružnici, která je parametrizovaná proměnnou ${\displaystyle \scriptstyle v}$. Máme-li na kružnici ${\displaystyle \scriptstyle M}$ zvolen pevně jistý počáteční bod, tak mu můžeme přiřadit hodnotu ${\displaystyle \scriptstyle v=0}$. Pokud zvětšujeme parametr ${\displaystyle \scriptstyle v}$ postupně od nuly do ${\displaystyle \scriptstyle 2\pi }$, tak projdeme všechny body kružnice. Každému bodu ${\displaystyle \scriptstyle m_{0}\in M}$ kružnice je tak jednoznačně přiřazeno jisté číslo ${\displaystyle \scriptstyle v_{0}\in [0,2\pi )}$. Tento vztah budeme v tomto oddíle vyjadřovat zápisem ${\displaystyle \scriptstyle m_{0}=m(v_{0})}$. Kružnice je jednorozměrná křivka a pokud ji vnoříme do trojrozměrného prostoru ${\displaystyle \scriptstyle \mathbb {R} ^{3}}$, tak jí můžeme ztotožnit s množinou ${\displaystyle \scriptstyle \{(x(0,v),y(0,v),z(0,v))|v\in [0,2\pi )\}}$. V takovém případě má počáteční bod kružnice souřadnice ${\displaystyle \scriptstyle \{(x(0,0),y(0,0),z(0,0))\}}$ a souřadnice ${\displaystyle \scriptstyle (x(v),y(v),z(v))}$ bodu ${\displaystyle \scriptstyle m(v)}$ mají tvar

${\displaystyle x(v)=\cos(v),\quad y(v)=\sin(v),\quad z(v)=0}$.

Jestliže si nyní ukotvíme parametr ${\displaystyle \scriptstyle v}$ a položíme ho rovno číslu ${\displaystyle \scriptstyle v_{0}=konst.}$, tak lze parametrické rovnice Möbiovy křivky přepsat do tvaru

${\displaystyle {\begin{array}{rcl}x(u)&=&\cos(v_{0})+u\,(\cos({\frac {v_{0}}{2}})\cos(v_{0})),\\y(u)&=&\sin(v_{0})+u\,(\cos({\frac {v_{0}}{2}})\sin(v_{0})),\\z(u)&=&u\,\sin({\frac {v_{0}}{2}}),\end{array}}}$

což je parametrické vyjádření úsečky ve trojrozměrném prostoru (parametr ${\displaystyle \scriptstyle u}$ probíhá omezený interval od −1/2 do 1/2). Proměnná ${\displaystyle \scriptstyle u}$ tedy parametrizuje vlákno; udává „vzdálenost“ bodu úsečky od jejího středu. Zaveďme pro prvky vlákna podobné značení, jaké jsme přijali pro prvky bázové variety. Konkrétně bod ${\displaystyle \scriptstyle f_{0}}$ ve „vzdálenosti“ ${\displaystyle \scriptstyle u_{0}}$ od středu úsečky vyjadřujme vztahem ${\displaystyle \scriptstyle f_{0}=f(u_{0})}$.

Uvažujme nyní nějaký konkrétní bod Möbiovy pásky, např. bod ${\displaystyle \scriptstyle p_{3}}$ na Obr. 1. Nechť jeho souřadnice znějí ${\displaystyle \scriptstyle (x(u_{3},v_{3}),y(u_{3},v_{3}),z(u_{3},v_{3}))}$ pro nějaké ${\displaystyle \scriptstyle u_{3}}$ a ${\displaystyle \scriptstyle v_{3}}$. Za projekci tohoto bodu na bázovou varietu položíme bod na kružnici, jehož vzdálenost od počátečního bodu kružnice je rovna ${\displaystyle \scriptstyle v_{3}}$. Pokud si za počáteční bod kružnice zvolíme bod ${\displaystyle \scriptstyle m_{1}}$ na Obr. 1, pro nějž platí ${\displaystyle \scriptstyle m_{1}=m(0)}$, tak projekcí bodu ${\displaystyle \scriptstyle p_{3}}$ je bod ${\displaystyle \scriptstyle m_{3}=m(v_{3})}$. V návaznosti na tento postup si tak zavedeme projekci ${\displaystyle \scriptstyle \pi :E\to M}$ vztahem

${\displaystyle \pi ((x(u,v),y(u,v),z(u,v)))=m(v),\quad \forall u\in [-1/2,1/2],\quad \forall v\in [0,2\pi )}$.

Projekce nám tak smaže veškerou informaci o vlákně skrytou v proměnné ${\displaystyle \scriptstyle u}$.

Lokální trivializace

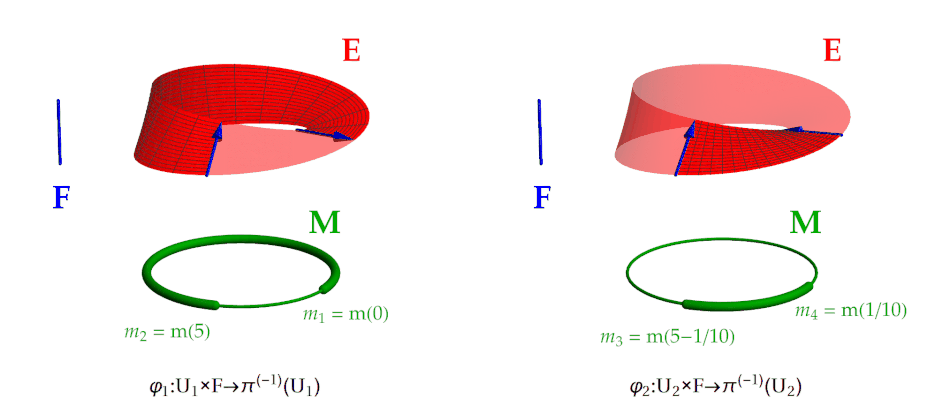
Zbývá nám určit lokální trivializace, jež sestávají z okolí pokrývajících bázovou varietu a k nim přiřazených zobrazení splňujících dodatečné podmínky. Za pokrytí kružnice bychom si mohli zvolit dvojici okolí

${\displaystyle U_{1}=\{m\in M|m=m(v),v\in (0,\,5)\},\quad U_{2}=\{m\in M|m=m(v),v\in \left(5-{\frac {1}{10}},\,2\pi +{\frac {1}{10}}\right)\}}$.

Pokud bychom uvažovali bázovou varietu ${\displaystyle \scriptstyle M}$ coby kružnici vloženou do ${\displaystyle \scriptstyle \mathbb {R} ^{3}}$, tak by šlo vyjádřit tato okolí ve tvaru

${\displaystyle U_{1}=\{(\cos(v),\sin(v),0)|v\in (0,\,5)\},\quad U_{2}=\{(\cos(v),\sin(v),0)|v\in \left(5-{\frac {1}{10}},\,2\pi +{\frac {1}{10}}\right)\}}$.

Meze intervalů jsme zvolili více méně libovolně, důležité je, aby tyto intervaly byly otevřené a jejich sjednocení bylo nadmnožinou intervalu ${\displaystyle \scriptstyle (0,2\pi )}$. Okolí bychom si mohli zvolit i více, rozhodně ne však méně. Později si ukážeme, že jediné okolí pokrývající kružnici M nelze pro zavedení lokálních trivializací použít. Pro aktuální volbu okolí nyní stačí za lokální trivializace vzít zobrazení ${\displaystyle \scriptstyle \varphi _{1}:U_{1}\times F\to \pi ^{(-1)}(U_{1})}$, ${\displaystyle \scriptstyle \varphi _{2}:U_{2}\times F\to \pi ^{(-1)}(U_{2})}$, jejichž předpis v parametrizaci pomocí proměnných ${\displaystyle \scriptstyle u,v}$ zní

${\displaystyle \varphi _{1}(m,f)=(x(u,v),y(u,v),z(u,v)),\quad {\text{kde}}\quad m=m(v),\ f=f(u),\quad \forall u\in [-1/2,\,1/2],\ \forall v\in [0,\,5)}$.

${\displaystyle \varphi _{2}(m,f)=(x(u,v),y(u,v),z(u,v)),\quad {\text{kde}}\quad m=m(v),\ f=f(u),\quad \forall u\in [-1/2,\,1/2],\ \forall v\in [5-1/10,2\pi +1/10)}$.

Parametrické rovnice Möbiovy pásky jsou tedy v podstatě lokálními trivializacemi. Zobrazení ${\displaystyle \scriptstyle \varphi _{1}}$ vezme jednak bod kružnice ${\displaystyle \scriptstyle m=m(v)}$ parametrizovaný hodnotou ${\displaystyle \scriptstyle v\in (0,5)}$, jednak bod typického vlákna ${\displaystyle \scriptstyle f=f(u)}$ parametrizovaný hodnotou ${\displaystyle \scriptstyle u\in [-1/2,1/2]}$, a této dvojici prvků přiřadí bod Möbiovy pásky, jehož souřadnice ${\displaystyle \scriptstyle (x(u,v),y(u,v),z(u,v))}$ se získají z parametrických rovnic. Trivializace ${\displaystyle \scriptstyle \varphi _{2}:U_{2}\times F\to \pi ^{(-1)}(U_{2})}$ se chová podobně, akorát její definiční obor je omezen na hodnoty ${\displaystyle \scriptstyle u\in [-1/2,1/2]}$ a ${\displaystyle \scriptstyle v\in (5-1/10,2\pi +1/10)}$. Pro názornost jsou pokrývající okolí i působení lokálních trivializací vykreslena na Obr. 3.

Zodpovězme nyní otázku, proč jsme uvážili dvě okolí ${\displaystyle \scriptstyle U_{1},U_{2}}$ namísto jednoho ${\displaystyle \scriptstyle U}$, které by pokrylo celou kružnici a které by mělo tvar

${\displaystyle U=\{m\in M|m=m(v),v\in [0,2\pi )\}=M}$.

Množina ${\displaystyle \scriptstyle U}$ je zjevně pokrývající a otevřená (celá množina vždy patří do své topologie a splňuje tak podmínku otevřenosti). Co nám tedy brání ji použít? Potíž je v tom, že odpovídající lokální trivializace ${\displaystyle \scriptstyle \varphi }$ by nebyla na celém svém definičním oboru hladké zobrazení. Abychom toto nahlédli mějme analogicky předchozímu případu

${\displaystyle \varphi (m,f)=(x(u,v),y(u,v),z(u,v)),\quad {\text{kde}}\quad m=m(v),\ f=f(u),\quad \forall u\in [-1/2,1/2],\ \forall v\in [0,2\pi )}$.

Při obejití kružnice se dostaneme zpět na počátek a musí tedy platit, že hodnoty lokální trivializace pro ${\displaystyle \scriptstyle v=0}$ a ${\displaystyle \scriptstyle v=2\pi }$ se při ukotveném ${\displaystyle \scriptstyle u=u_{0}=konst.}$ rovnají. Hodnota ${\displaystyle \scriptstyle 2\pi }$ přísně vzato neleží v definičním oboru a tato podmínka proto zní

${\displaystyle \varphi (m(0),f(u_{0}))=\lim _{v\to 2\pi _{-}}\varphi (m(v),f(u_{0}))}$.

Položíme-li ${\displaystyle \scriptstyle u_{0}=1/2}$, tak se levá strana redukuje do tvaru ${\displaystyle \scriptstyle \varphi (m(0),f(1/2))=(1.5,0,0)}$, zatímco pravá strana přechází na tvar ${\displaystyle \scriptstyle (0.5,0,0)}$. Rovnost tedy viditelně nenastává a s jediným pokrývajícím okolím Möbiovy pásky si tak nevystačíme. Graficky lze nespojitost zobrazení ${\displaystyle \scriptstyle \varphi :M\times F\to E}$ vidět na animaci v Obr. 2, kde šipka „generující“ pásku na počátku směřuje ven, při oběhnutí kružnice však směřuje dovnitř pomyslného kruhu.

Naše volba dvou okolí s danými trivializacemi problém nespojitosti zobrazení obchází. Zatímco u jednoho okolí ${\displaystyle \scriptstyle U=M}$ mělo toto topologii kruhu a daná trivializace musela být „spojitá v počátečním bodě“, tak pokud použijeme okolí dvě, tak každé z nich má topologii úsečky (bez koncových bodů) a o žádnou spojitost v „počátečním bodě“ se nemusíme starat.

• 

  Obr. 3: Möbiova páska spolu s lokálními trivializacemi. Vlevo je zobrazeno okolí ${\displaystyle \scriptstyle U_{1}}$ bázové variety ${\displaystyle \scriptstyle M}$ coby tlustší úsek kružnice ohraničený body ${\displaystyle \scriptstyle m_{1}}$ a ${\displaystyle \scriptstyle m_{2}}$. Odpovídající kus Möbiovy pásky, který je zobrazen na toto okolí a vlákno pomocí lokální trivializace ${\displaystyle \scriptstyle \varphi _{1}}$, je pak vyobrazen sytou barvou. Trivializace přitom působí takovým způsobem, že daný úsek pásky je zobrazen na "obdélník" ${\displaystyle \scriptstyle U_{1}\times F}$. Mřížka pokrývající daný úsek Möbiovy pásky je tak působením lokální trivializace "narovnána" na pravoúhlou mřížku pokrývající obdélník ${\displaystyle \scriptstyle [-1/2,1/2]\times (0,5)}$. Vpravo je pak možno vidět analogickou situaci pro okolí ${\displaystyle \scriptstyle U_{2}}$ s trivializací ${\displaystyle \scriptstyle \varphi _{2}}$. Povšimněme si i směrů šipek ohraničujících dané úseky Möbiovy pásky.

Přechodové funkce

Okolí ${\displaystyle \scriptstyle U_{1}}$ a ${\displaystyle \scriptstyle U_{2}}$ se překrývají v oblastech ${\displaystyle \scriptstyle (5-1/10,5)}$ a ${\displaystyle \scriptstyle (2\pi ,2\pi +1/10)}$. Označme si první interval písmenem ${\displaystyle \scriptstyle A=(5-1/10,5)}$ a druhý interval podobně písmenem ${\displaystyle \scriptstyle B=(2\pi ,2\pi +1/10)}$. Pro úplnost si odvodíme tvar přechodových funkcí ${\displaystyle \scriptstyle \tau _{12}}$ a ${\displaystyle \scriptstyle \tau _{21}}$. Vzhledem k tomu, že jedna je inverzí druhé, stačí spočíst ${\displaystyle \scriptstyle \tau _{12}:U_{1}\cap U_{2}\times F\to F}$. Zde je nutno pro každý z obou intervalů A a B hledat tvar přechodové funkce zvlášť. Pro všechny body ${\displaystyle \scriptstyle m=m(v)\in M}$, kde ${\displaystyle \scriptstyle v\in A}$, a pro všechny prvky vlákna ${\displaystyle \scriptstyle f=f(u)\in F}$, ${\displaystyle \scriptstyle u\in [-1/2,1/2]}$, platí

${\displaystyle (\varphi _{2}^{-1}\circ \varphi _{1})(m,f)=\varphi _{2}^{-1}((x(u,v),y(u,v),z(u,v)))=(m,f)}$.

Přechodová funkce ${\displaystyle \scriptstyle \tau _{12}^{A}:F\to F}$ je tedy identickým zobrazením. Explicitně,

${\displaystyle \tau _{12}^{m}(f(u))=f(u),\quad m=m(v),\ v\in A,\quad \forall u\in [-1/2,1/2]}$.

Podobně postupujeme i pro interval B, zde však musíme být více na pozoru. Proměnná ${\displaystyle \scriptstyle v}$, parametrizující kružnici, nabývá hodnot mezi nulou a ${\displaystyle \scriptstyle 2\pi }$. V intervalu B se však nacházejí čísla mimo tyto meze. Protože hodnotě ${\displaystyle \scriptstyle 2\pi +v\in [2\pi ,4\pi )}$ by měl odpovídat stejný bod kružnice jako hodnotě ${\displaystyle \scriptstyle v\in [0,2\pi )}$, vyjádřeme si proměnnou ${\displaystyle \scriptstyle v\in B}$ explicitně ve tvaru ${\displaystyle \scriptstyle 2\pi +v}$, kde už ${\displaystyle \scriptstyle v\in [0,1/10)\subset [0,2\pi )}$. Při tomto vyjádření přecházejí goniometrické funkce do tvarů

${\displaystyle \cos \left({\frac {v}{2}}\right)\rightarrow \cos \left({\frac {2\pi +v}{2}}\right)=\cos \left(\pi +{\frac {v}{2}}\right)=-\cos \left({\frac {v}{2}}\right)}$,

${\displaystyle \sin \left({\frac {v}{2}}\right)\rightarrow \sin \left({\frac {2\pi +v}{2}}\right)=\sin \left(\pi +{\frac {v}{2}}\right)=-\sin \left({\frac {v}{2}}\right)}$.

Vyjádření lokální trivializace ${\displaystyle \scriptstyle \varphi _{2}}$ tak přejde do tvaru

${\displaystyle {\begin{array}{rcl}x(u,v)&=&(1-u\cos({\frac {v}{2}}))\cos(v),\\y(u,v)&=&(1-u\cos({\frac {v}{2}}))\sin(v),\\z(u,v)&=&-u\,\sin({\frac {v}{2}}),\end{array}}}$

kde nyní parametr ${\displaystyle \scriptstyle v}$ nenabývá hodnot z intervalu B, ale z intervalu ${\displaystyle \scriptstyle [0,1/10)}$. Vidíme, že znaménko minus, objevivší se z úpravy goniometrických funkcí, můžeme přidružit k proměnné ${\displaystyle \scriptstyle u}$. Máme-li pevně zadán bod ${\displaystyle \scriptstyle (x,y,z)}$ Möbiovy pásky, jehož parametry v trivializaci ${\displaystyle \scriptstyle \varphi _{1}}$ mají hodnoty ${\displaystyle \scriptstyle u=u_{1}\in [-1/2,1/2]}$ a ${\displaystyle \scriptstyle v=v_{1}\in [0,1/10)}$, tak v trivializaci ${\displaystyle \scriptstyle \varphi _{2}}$ je tentýž bod popsán parametry o hodnotách ${\displaystyle \scriptstyle u=u_{2}\in [-1/2,1/2]}$ a ${\displaystyle \scriptstyle v=v_{2}\in [0,1/10)}$, kde však

${\displaystyle u_{2}=-u_{1},\quad v_{2}=v_{1}}$.

Z těchto vztahů okamžitě vidíme, že na intervalu B přechodová funkce ${\displaystyle \scriptstyle \tau _{12}^{B}:F\to F}$ efektivně obrací hodnotu parametru ${\displaystyle \scriptstyle u}$

${\displaystyle \tau _{12}^{m}(f(u))=f(-u),\quad m=m(v),\ v\in B,\quad \forall u\in [-1/2,1/2]}$.

Toto obracení parametru je explicitní vyjádření nespojitosti, se kterou jsme se setkali u zobrazení ${\displaystyle \scriptstyle \varphi :M\times F\to E}$ v předchozím pododdíle o lokálních trivializacích. Graficky pak obracení parametru ${\displaystyle \scriptstyle u}$ při přechodu od jedné trivializace ke druhé na intervalu ${\displaystyle \scriptstyle [0,1/10)}$ můžeme odtušit ze směru ohraničující šipky na Obr. 3, kde pro trivializaci ${\displaystyle \scriptstyle \varphi _{1}}$ směřuje daná šipka ven, zatímco u trivializace ${\displaystyle \scriptstyle \varphi _{2}}$ tato šipka směřuje dovnitř.

Jen tak na okraj, v případě válce (kde neuvažujeme jeho podstavy) k žádné podobné nespojitosti nedochází a celý válec tak lze popsat jediným okolím a jedinou lokální trivializací. Válec je tedy příkladem triviálního fibrovaného prostoru. Pokud bychom i přesto pokrývali válec dvěma okolími jako v případě Möbiovy pásky výše a zvolili bychom si přirozenou parametrizaci válcové plochy, tak přechodová funkce by byla na obou intervalech A i B identické zobrazení.

Na závěr tedy můžeme vyjádřit předpis přechodové funkce na celém průniku okolí ${\displaystyle \scriptstyle U_{1}}$ a ${\displaystyle \scriptstyle U_{2}}$ pro Möbiovu pásku způsobem

${\displaystyle \tau _{12}^{m(v)}(f(u))={\begin{cases}f(u)&v\in A,\\f(-u)&v\in B.\end{cases}}}$

Rekonstrukce fibrovaného prostoru ze znalosti přechodových zobrazení

V tomto oddíle si ukážeme důležitost přechodových funkcí definovaných výše. Zrekonstruujeme totiž fibrovaný prostor ${\displaystyle \scriptstyle (E,M,F,\pi )}$ jen na základě znalosti bázové variety ${\displaystyle \scriptstyle M}$, jejího otevřeného pokrytí ${\displaystyle \scriptstyle \{U_{\alpha }\}_{\alpha }}$, typického vlákna ${\displaystyle \scriptstyle F}$ a přechodových zobrazení ${\displaystyle \scriptstyle \tau _{\alpha \beta }}$ tvořících strukturní grupu ${\displaystyle \scriptstyle G}$. K plnému určení fibrovaného prostoru tedy ještě musíme najít totální prostor ${\displaystyle \scriptstyle E}$, projekci ${\displaystyle \scriptstyle \pi }$ a lokální trivializace ${\displaystyle \scriptstyle \varphi _{\alpha }}$. Postup je následující:

Nejprve si definujme množinu

${\displaystyle X=\bigcup _{\alpha }(U_{\alpha }\times F)}$

a zaveďme si na ní relaci ekvivalence ${\displaystyle \scriptstyle \sim }$, kdy prvky ${\displaystyle \scriptstyle (m,f)\in U_{\alpha }\times F}$ a ${\displaystyle \scriptstyle (m',f')\in U_{\alpha }\times F}$ jsou ekvivalentní ${\displaystyle \scriptstyle (m,f)\sim (m',f')}$ právě tehdy, když ${\displaystyle \scriptstyle m=m'}$ a současně existuje ${\displaystyle \scriptstyle \tau _{\alpha \beta }^{(m)}\in G}$ tak, že ${\displaystyle \scriptstyle f'=\tau _{\alpha \beta }^{(m)}f}$. Aby tento vztah byl skutečně ekvivalencí, musejí přechodové funkce splňovat požadavky:

1. ${\displaystyle \tau _{\alpha \alpha }=\mathrm {Id} }$,
2. ${\displaystyle \tau _{\alpha \beta }^{-1}=\tau _{\beta \alpha }}$,
3. ${\displaystyle \tau _{\alpha \gamma }=\tau _{\beta \gamma }\circ \tau _{\alpha \beta }}$,

kde ${\displaystyle \scriptstyle \mathrm {Id} }$ značí identické zobrazení. Totální prostor ${\displaystyle \scriptstyle E}$ poté definujeme jako množinu ${\displaystyle \scriptstyle X}$ faktorizovanou podle právě uvedené ekvivalence

${\displaystyle E=X/_{\sim }}$.

Každý prvek totálního prostoru je tedy třída ekvivalence. Třídu ekvivalence, jež obsahuje prvek ${\displaystyle \scriptstyle (m,f)}$ si budeme značit ${\displaystyle \scriptstyle [m,f]}$. Projekci ${\displaystyle \scriptstyle \pi :E\to M}$ definujeme přirozeným způsobem

${\displaystyle \pi ([m,f])=m}$.

Podobně přirozeně nadefinujeme i lokální trivializace ${\displaystyle \scriptstyle \varphi _{\alpha }:U_{\alpha }\times F\to \pi ^{-1}(U_{\alpha })}$ a sice

${\displaystyle \varphi _{\alpha }(m,f)=[m,f]}$.

Lze jednoduše ověřit, že takto definované objekty skutečně vyhovují definici fibrovaného prostoru.

Význačné příklady fibrovaných prostorů

V tomto oddíle jsou zmíněny některé druhy fibrovaných prostorů, z nichž nejvýraznějšími jsou patrně tečný bandl a hlavní fibrovaný prostor.

Vektorový fibrovaný prostor

Vektorový fibrovaný prostor (angl. vector bundle) je fibrovaný prostor, jehož typickým vláknem je vektorový prostor. Přechodové funkce v tomto případě tvoří strukturní grupu všech nesingulárních matic odpovídajících rozměrů. Je-li typické vlákno reálný vektorový prostor dimenze k, tj. ${\displaystyle \scriptstyle F=\mathbb {R} ^{k}}$, tak strukturní grupa je rovna maticové grupě ${\displaystyle \scriptstyle GL(\mathbb {R} ,k)}$. Podobně, pokud je typické vlákno rovno komplexnímu vektorovému prostoru ${\displaystyle \scriptstyle F=\mathbb {C} ^{k}}$, tak strukturní grupa je ${\displaystyle \scriptstyle GL(\mathbb {C} ,k)}$. Číslo k se nazývá dimenze vlákna a značí se, poněkud nekonzistentně, symbolem ${\displaystyle \scriptstyle \dim E}$.^[1] (Ačkoli dimenze totálního prostoru E je rovna n + k, kde n je dimenze bázové variety M.) Důležitým příkladem vektorového fibrovaného prostoru je tečný fibrovaný prostor. Jiným příkladem je normálový fibrovaný prostor. Oba druhy jsou popsány v následujících pododdílech.

Tečný fibrovaný prostor

Jedním z důležitých příkladů fibrovaných prostorů je tzv. tečný fibrovaný prostor (někdy též tečný bandl, angl. tangent bundle), k němuž dojdeme následujícím postupem. Uvažujme nějakou (reálnou) diferencovatelnou varietu ${\displaystyle \scriptstyle M}$ konečné dimenze ${\displaystyle \scriptstyle \dim M=n}$. V každém bodě ${\displaystyle \scriptstyle m}$ této variety je definován tečný prostor ${\displaystyle \scriptstyle T_{m}M}$, což je vektorový prostor všech tečných vektorů k varietě ${\displaystyle \scriptstyle M}$ v bodě ${\displaystyle \scriptstyle m}$. Disjunktním sjednocením všech tečných prostorů

${\displaystyle TM=\coprod _{m\in M}T_{m}M}$

získáme totální prostor tečného fibrovaného prostoru. Disjunktním sjednocením je zde přitom míněno sjednocení, kde prvek z ${\displaystyle \scriptstyle TM}$ si „pamatuje“ nejen to, kam coby tečný vektor míří, ale i z jakého bodu variety vychází. Informaci o bodu variety, ze kterého daný prvek ${\displaystyle \scriptstyle p\in TM}$ vychází, nám přitom podá projekce ${\displaystyle \scriptstyle \pi :TM\to M}$. Matematicky zapsáno

${\displaystyle p\in T_{m}M\quad \Rightarrow \quad \pi (p)=m}$.

Bázovou varietou je tedy samotná varieta ${\displaystyle \scriptstyle M}$ a vláknem je vektorový prostor ${\displaystyle \scriptstyle \mathbb {R} ^{n}}$, neboť všechny tečné prostory ${\displaystyle \scriptstyle T_{m}M}$ pro libovolné ${\displaystyle \scriptstyle m\in M}$ jsou izomorfní ${\displaystyle \scriptstyle \mathbb {R} ^{n}}$.

Abychom mohli zavést lokální trivializace, uvažme nějaké otevřené pokrytí ${\displaystyle \scriptstyle \{U_{\alpha }\}_{\alpha }}$ variety ${\displaystyle \scriptstyle M}$ a z něho uvažujme právě jedno konkrétní okolí ${\displaystyle \scriptstyle U_{\alpha }}$ se souřadnicemi ${\displaystyle \scriptstyle \psi _{\alpha }:U_{\alpha }\to \mathbb {R} ^{n}}$. Souřadnice ${\displaystyle \scriptstyle \{x^{\mu }\}_{\mu =1}^{n}}$ bodu ${\displaystyle \scriptstyle m\in U_{\alpha }\subset M}$ variety tedy obdržíme ze vzorce ${\displaystyle \scriptstyle \{x^{\mu }\}_{\mu =1}^{n}=\psi _{\alpha }(m)}$. Každý bod variety ${\displaystyle \scriptstyle M}$ v okolí ${\displaystyle \scriptstyle U_{\alpha }}$ je tedy jednoznačně popsán ${\displaystyle \scriptstyle n}$-ticí čísel. Co víc, za bázi tečného prostoru ${\displaystyle \scriptstyle T_{m}M}$ si můžeme vzít derivace ${\displaystyle \scriptstyle \{\partial /\partial {x^{\mu }}\}_{\mu =1}^{n}}$. Každý vektor ${\displaystyle \scriptstyle X=X^{\mu }\partial /\partial x^{\mu }}$ z ${\displaystyle \scriptstyle T_{m}M}$ je tedy také určen ${\displaystyle \scriptstyle n}$-ticí čísel ${\displaystyle \scriptstyle \{X^{\mu }\}_{\mu =1}^{n}}$. Pro jednoznačnou identifikaci bodu ${\displaystyle \scriptstyle p}$ z množiny ${\displaystyle \scriptstyle \pi ^{(-1)}(U_{\alpha })}$ (tj. ze vzoru okolí ${\displaystyle \scriptstyle U_{\alpha }}$ při projekci ${\displaystyle \scriptstyle \pi }$) je tedy třeba znát ${\displaystyle \scriptstyle 2n}$ čísel

${\displaystyle (x^{1},\ldots ,x^{n},X^{1},\ldots ,X^{n})}$.

Za lokální trivializaci ${\displaystyle \scriptstyle \varphi _{\alpha }:U_{\alpha }\times \mathbb {R} ^{n}\to \pi ^{(-1)}(U_{\alpha })}$ tak můžeme vzít zobrazení, jehož inverze má v souřadnicích ${\displaystyle \scriptstyle \psi _{\alpha }}$ tvar

${\displaystyle \varphi _{\alpha }^{-1}(p)=(x^{1},\ldots ,x^{n},X^{1},\ldots ,X^{n})}$.

Tímto způsobem obdržíme lokální trivializace pro všechna pokrývací okolí. Tečný fibrovaný prostor je tedy fibrovaný prostor určený čtveřicí ${\displaystyle \scriptstyle (TM,M,\mathbb {R} ^{n},\pi )}$ a danými lokálními trivializacemi.

Řez tečného fibrovaného prostoru se nazývá vektorové pole. Každému bodu variety ${\displaystyle \scriptstyle M}$ je tedy přiřazen nějaký vektor a toto přiřazení je hladké.

Normálový fibrovaný prostor

Nechť ${\displaystyle \scriptstyle M}$ je ${\displaystyle \scriptstyle n}$-rozměrná diferencovatelná varieta vložená do prostoru ${\displaystyle \scriptstyle \mathbb {R} ^{n+k}}$. Dále nechť ${\displaystyle \scriptstyle N_{m}M}$ je ortogonální doplněk k ${\displaystyle \scriptstyle T_{m}M}$ ve vektorovém prostoru ${\displaystyle \scriptstyle \mathbb {R} ^{n+k}}$, kde ${\displaystyle \scriptstyle T_{m}M}$ značí tečný vektorový prostor k varietě ${\displaystyle \scriptstyle M}$ v bodě ${\displaystyle \scriptstyle m\in M}$. Platí tedy

${\displaystyle N_{m}M=\{v\in \mathbb {R} ^{n+k}|(\forall u\in T_{m}M)(v\cdot u=0)\}}$,

kde tečka značí standardní skalární součin. Z předchozího plyne, že vektorový prostor ${\displaystyle \scriptstyle N_{m}M}$ je izomorfní prostoru ${\displaystyle \scriptstyle \mathbb {R} ^{k}}$. Disjunktním sjednocením všech množin vznikne normálový fibrovaný prostor ${\displaystyle \scriptstyle NM}$ (angl. normal bundle), jehož typickým vláknem je ${\displaystyle \scriptstyle \mathbb {R} ^{k}}$. Explicitně tedy

${\displaystyle NM=\coprod _{p\in M}N_{p}M}$.

Duální fibrovaný prostor

Mějme vektorový fibrovaný prostor ${\displaystyle \scriptstyle E{\stackrel {\pi }{\to }}M}$ s vláknem ${\displaystyle \scriptstyle F}$. K vektorovému prostoru ${\displaystyle \scriptstyle F}$ můžeme uvažovat prostor ${\displaystyle \scriptstyle F^{\ast }}$ k němu duální, jenž je tvořen všemi lineárními funkcionály. Tento prostor má stejnou dimenzi jako ${\displaystyle \scriptstyle F}$ a fibrovaný prostor, kde za vlákno vezmeme ${\displaystyle \scriptstyle F^{\ast }}$, nazýváme duální fibrovaný prostor (angl. dual bundle). Speciálním druhem duálního fibrovaného prostoru je kotečný fibrovaný prostor, jenž je definován níže.

Kotečný fibrovaný prostor

Ke každému tečnému prostoru ${\displaystyle \scriptstyle T_{m}M}$ existuje prostor duální ${\displaystyle \scriptstyle T_{m}^{\ast }M}$, tvořený lineárními funkcionály definovanými nad vektory z ${\displaystyle \scriptstyle T_{m}M}$. Tomuto duálnímu prostoru se říká kotečný prostor k varietě ${\displaystyle \scriptstyle M}$ v bodě ${\displaystyle \scriptstyle m}$. Postupem analogickým tomu pro tečný fibrovaný prostor můžeme definovat tzv. kotečný fibrovaný prostor (někdy též kotečný bandl, angl. cotangent bundle). V případě kotečného fibrovaného prostoru je za bázovou varietu zvolena (reálná) diferencovatelná varieta ${\displaystyle \scriptstyle M}$ dimenze ${\displaystyle \scriptstyle \dim M=n}$, totální prostor se definuje jako disjunktní sjednocení duálních prostorů

${\displaystyle T^{\ast }M=\coprod _{m\in M}T_{m}^{\ast }M}$

a za vlákno se bere množina ${\displaystyle \scriptstyle \mathbb {R} ^{n}}$. Tato množina je totiž izomorfní duálnímu prostoru ${\displaystyle \scriptstyle T_{m}^{\ast }M}$ pro libovolný bod variety ${\displaystyle \scriptstyle m\in M}$. Projekce ${\displaystyle \scriptstyle \pi :T^{\ast }M\to M}$ je volena tak, aby pro každý prvek z ${\displaystyle \scriptstyle T^{\ast }M}$ vrátila bod variety, odkud tento prvek pochází. To jest

${\displaystyle \omega \in T_{m}^{\ast }M\quad \Rightarrow \quad \pi (\omega )=m}$.

Jak je zmíněno v předchozím pododdíle o tečném fibrovaném prostoru, pro každý tečný prostor ${\displaystyle \scriptstyle T_{m}M}$ k varietě ${\displaystyle \scriptstyle M}$ v bodě ${\displaystyle \scriptstyle m}$, kdy se bod ${\displaystyle \scriptstyle m}$ nachází v nějakém pokrývacím okolí ${\displaystyle \scriptstyle U_{\alpha }\subset M}$ popsaném souřadnicemi ${\displaystyle \scriptstyle \psi _{\alpha }(m)=\{x^{\mu }\}_{\mu =1}^{n}}$, můžeme za bázi tečného prostoru vzít množinu ${\displaystyle \scriptstyle \{\partial /\partial {x^{\mu }}\}_{\mu =1}^{n}}$ derivací podle daných souřadnic. V duálním prostoru ${\displaystyle \scriptstyle T_{m}^{\ast }M}$ dále můžeme uvažovat bázi souřadnicových funkcionálů ${\displaystyle \scriptstyle \{\mathrm {d} x^{\mu }\}_{\mu =1}^{n}}$, jejichž působení na vektorech alias derivacích lze vyjádřit elegantně ve tvaru

${\displaystyle \mathrm {d} x^{\mu }\left({\frac {\partial }{\partial x^{\nu }}}\right)=\delta _{\nu }^{\mu }}$,

kde ${\displaystyle \scriptstyle \delta _{\nu }^{\mu }}$ označuje Kroneckerovo delta. Každý lineární funkcionál ${\displaystyle \scriptstyle \omega (m)}$ z duálního prostoru ${\displaystyle \scriptstyle T_{m}^{\ast }M}$ tak lze zapsat ve tvaru ${\displaystyle \scriptstyle \omega (m)=\omega _{\mu }\,\mathrm {d} x^{\mu }}$ a je tak plně určen souřadnicemi ${\displaystyle \scriptstyle \{\omega _{\mu }\}_{\mu =1}^{n}}$. Lokální trivializaci ${\displaystyle \scriptstyle \varphi _{\alpha }:U_{\alpha }\times \mathbb {R} ^{n}\to \pi ^{(-1)}(U_{\alpha })}$ tak můžeme zavést způsobem, že její inverze nabývá tvaru

${\displaystyle \varphi _{\alpha }^{-1}(\omega )=(x^{1},\ldots ,x^{n},\omega _{1},\ldots ,\omega _{n})}$,

kde ${\displaystyle \scriptstyle (x^{1},\ldots ,x^{n})}$ jsou souřadnice bodu ${\displaystyle \scriptstyle m\in U_{\alpha }\subset M}$. Tuto konstrukci lokální trivializace můžeme provést pro všechna pokrývací okolí. Kotečný fibrovaný prostor je tedy fibrovaný prostor určený čtveřicí ${\displaystyle \scriptstyle (T^{\ast }M,M,\mathbb {R} ^{n},\pi )}$ a danými lokálními trivializacemi.

Řez kotečného fibrovaného prostoru se nazývá diferenciální 1-forma. Každému bodu variety ${\displaystyle \scriptstyle M}$ je tedy přiřazen nějaký lineární funkcionál na ${\displaystyle \scriptstyle \mathbb {R} ^{n}}$ a toto přiřazení je hladké.

Hlavní fibrovaný prostor

Fibrovaný prostor ${\displaystyle \scriptstyle (P,M,F,\pi )}$, jehož typické vlákno F je rovno strukturní grupě G a ta je navíc grupou Lieovou, nazýváme hlavní fibrovaný prostor (angl. principal bundle nebo G bundle) a značíme též symbolem

${\displaystyle P(M,G)}$.

Totožnost vlákna a strukturní grupy nám umožňuje na totálním prostoru zavést pravou akci grupy, pomocí které lze mj. snadno popisovat tvar vláken nad jednotlivými body bázové variety. Předtím, než přejdeme k definici, si připomeňme, že lokální trivializace jsou zobrazení ${\displaystyle \scriptstyle \varphi _{\alpha }:U_{\alpha }\times G\to \pi ^{-1}(U_{\alpha })}$, jejichž inverze jsou dány předpisem