Foucaultovo kyvadlo

Foucaultovo kyvadlo, pojmenované po francouzském fyzikovi J. B. Léonu Foucaultovi, představuje důležitý experiment potvrzující otáčení planety Země kolem své osy.
Historie experimentu

Původní pokus byl proveden v roce 1851 v pařížském Pantheónu, kde bylo v kupoli zavěšeno závaží o hmotnosti 28 kilogramů na 68 metrů dlouhém laně. Doba kmitu kyvadla byla 16 sekund. Na závaží kyvadla byl hrot, kterým se do písku na podlaze zakresloval pohyb kyvadla. Pozorovatelé tak mohli vidět, jak se postupně mění rovina kyvu.
V roce 1851 bylo všeobecně známo, že se Země otáčí. Bylo také pozorováno zploštění Země na pólech. Foucaultovo kyvadlo však bylo prvním jasně viditelným důkazem a způsobilo tak velkou senzaci jak v odborných kruzích, tak u široké veřejnosti.
Na obou pólech Země se rovina kyvu nemění vzhledem k okolním hvězdám, zatímco Země se jednou za den zcela otočí. Vzhledem k Zemi se tedy rovina kyvu na severním nebo jižním pólu jednou za den zcela otočí po směru nebo proti směru hodinových ručiček. Pokud bychom Foucaultovo kyvadlo zavěsili na rovníku, rovina kyvu zůstane vzhledem k Zemi nezměněna. V ostatních zeměpisných šířkách se rovina kyvu vzhledem k Zemi sice otáčí, ale pomaleji, než na pólech.
Zeměpisná šířka je definována jako kladná a záporná (severní a jižní). Například rovina kyvu kyvadla na 30 ° jižní šířky při pohledu shora rotuje vzhledem k Zemi o 180 ° denně po směru hodinových ručiček.
Za účelem demonstrace zemské rotace bez komplikací, které přináší závislost na zeměpisné šířce, uvedl Foucault v roce 1852 gyroskop. Jeho rotor sleduje přímo hvězdy. Osa rotace se tak vrací do stejné polohy vzhledem k Zemi, a to bez ohledu na zeměpisnou šířku (není tedy ovlivněna sinusovým faktorem).

Foucaultovo kyvadlo je konstrukčně velmi náročné, protože i malá nepřesnost může způsobit další odchylky roviny kyvu, které pak převládnou nad vlivem zemské rotace. Kritické je také samotné spuštění kyvadla. To se provádí přepálením lanka, které drží kyvadlo ve výchozí poloze, čímž se zabrání nechtěným pohybům kyvadla do stran. Odpor vzduchu kyvadlo brzdí, proto jsou kyvadla v muzeích často elektromagneticky nebo jinak poháněna, případně opakovaně spouštěna.
Celý experiment byl uspořádán právě proto, aby dokázal existenci tohoto jevu, který Foucault teoreticky odvodil na základě předpokladů o vlivu Coriolisovy síly. Tato síla způsobuje vychylování kyvadla proti směru hodinových ručiček. Tento jev je důsledkem toho, že zvolená soustava (tedy otáčející se Země) není soustavou inerciální. Ve skutečnosti se totiž neotáčí kyvadlo, neboť kyvadlo si pouze zachovává rovinu kyvu, ale planeta Země se otáčí pod ním.
Exponáty v Česku

Foucaultovo kyvadlo je v různých velikostech a provedeních umístěno také v některých institucích a objektech v České republice:
- Nejstarší model sestavený fyzikem a astronomem Františkem Nábělkem s 22,35 metrů dlouhým lankem[1] je umístěn v Květné zahradě v Kroměříži
- Desetimetrové kyvadlo se nachází ve Hvězdárně a planetáriu v Hradci Králové.
- Jeden z exponátů, který v roce 2012 prošel rekonstrukcí, se nachází v budově České spořitelny v Hodoníně, kde je kyvadlo o délce 20,1 metrů zavěšeno uprostřed proskleného točitého schodiště a je volně přístupné v otevíracích hodinách České spořitelny.
- V Praze je kyvadlo umístěno:
- na 21 metrů dlouhém laně v budově ČVUT na Karlově náměstí
- v rekonstruované vodárenské věži na Letné
- na Matematicko-fyzikální fakultě Univerzity Karlovy v budově F Ke Karlovu 5 je od roku 2016 v zadním schodišti umístěno Foucaultovo kyvadlo nalezené v historických sbírkách Kabinetu výuky obecné fyziky MFF UK. To visí na ocelovém laně o délce 21,3 m, a má hmotnost 18 kg.
- Další Foucaultovo kyvadlo se nachází na Gymnáziu Brno, Křenová a je zavěšeno ve výšce zhruba 15 metrů.
- Foucaultovo kyvadlo na Přírodovědecké fakultě Univerzity Palackého v Olomouci má o hmotnost 37 kg na textilním laně o délce 25,5 metrů, které je trvale udržováno v pohybu pomocí elektromagnetu. Průchody kyvadla rovnovážnou polohou jsou sledovány laserovými závorami a elektromagnet je pak na základě těchto měření ovládán Arduinem.
- V roce 2020 bylo Foucaultovo kyvadlo instalováno ve vestibulu Gymnázia Dr. Josefa Pekaře v Mladé Boleslavi. [2]

Galerie
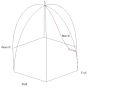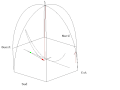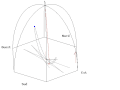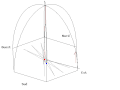
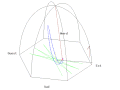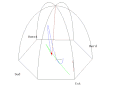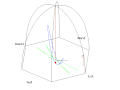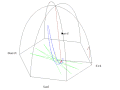
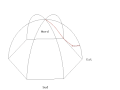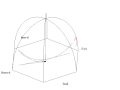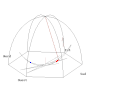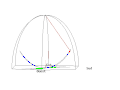
- Animace Foucaultova kyvadla z pařížského Panthéonu
- Standardní pohled
- Pohled z oscilační roviny
- Pohled ze Slunce
Reference
Související články
- Kyvadlo
- Léon Foucault
- Umberto Eco – autor knihy Foucaultovo kyvadlo (Il pendolo di Foucault)
Externí odkazy
 Obrázky, zvuky či videa k tématu Foucaultovo kyvadlo na Wikimedia Commons
Obrázky, zvuky či videa k tématu Foucaultovo kyvadlo na Wikimedia Commons - Co má společného Foucaultovo kyvadlo s počasím? Archivováno 30. 6. 2007 na Wayback Machine. na Astronomie.cz
- Online kamera kyvadla na univerzitě v Heidelbergu
- Online kamera kyvadla na univerzitě v Miskolci, Maďarsko Archivováno 14. 9. 2020 na Wayback Machine.
- Online kamera kyvadla na univerzitě v Osnabrücku Archivováno 10. 7. 2020 na Wayback Machine.
Média použitá na této stránce
Autor: Nbrouard, Licence: CC BY-SA 3.0
Animation of a fictitious pendulum of Foucault of 67 meters released at a distance of 50,25 meters (3/4 its length) in the east with a null speed. The rotation of the Earth is also exaggerated and corresponds to a rotation in 110 seconds. It corresponds to the view taken from the plane of oscillations: the terrestrial reference frame thus turns. But the shadow of a stick added at the center for ease of comprehension, rotates faster than the plane of oscillations. In this pseudo plan, the trace is not linear but corresponds to an ellipse. In this illustration, the pendulum is launched at noon at equinox. Thus the sun set is exactly six hours after the launch. Source of the Gnuplot animation is provided (GPL)
Autor: DemonDeLuxe (Dominique Toussaint), Licence: CC BY-SA 3.0
Animation of a Foucault pendulum (showing the sense of rotation on the southern hemisphere) Warning: This animation does not correpond to reality (see en:Talk:Foucault pendulum#Removed_incorrect_animation or fr:Discussion:Pendule de Foucault#Précession)
Autor: František Piliar, Licence: CC BY-SA 3.0
Foucaultovo kyvadlo, Rotunda v Květné zahradě, Kroměříž
Autor: Britchi Mirela, Licence: CC BY-SA 3.0
PANTHEON (The Pendule of Foucault), Paris
Autor: Nbrouard, Licence: CC BY-SA 3.0
Animation of a fictitious pendulum of Foucault of 67 meters released at a distance of 50,25 meters (3/4 its length) in the east with a null speed. The rotation of the Earth is also exaggerated and corresponds to a rotation in 110 seconds. It corresponds to the view taken from the plane of oscillations: the terrestrial reference frame thus turns. But the shadow of a stick added at the center for ease of comprehension, rotates faster than the plane of oscillations. In this pseudo plan, the trace is not linear but corresponds to an ellipse. In this illustration, the pendulum is launched at noon at equinox. Thus the sun set is exactly six hours after the launch. Source of the Gnuplot animation is provided (GPL)
Autor: Tomáš Opatrný, Licence: CC BY-SA 4.0
Foucaultovo kyvadlo na Přírodovědecké fakultě UP v Olomouci
Autor: Nbrouard, Licence: CC BY-SA 3.0
Animation of a fictitious pendulum of Foucault of 67 meters released at a distance of 50,25 meters (3/4 its length) in the east with a null speed. The rotation of the Earth is also exaggerated and corresponds to a rotation in 110 seconds. It corresponds to the view taken from the plane of oscillations: the terrestrial reference frame thus turns. But the shadow of a stick added at the center for ease of comprehension, rotates faster than the plane of oscillations. In this pseudo plan, the trace is not linear but corresponds to an ellipse. In this illustration, the pendulum is launched at noon at equinox. Thus the sun set is exactly six hours after the launch. Source of the Gnuplot animation is provided (GPL)