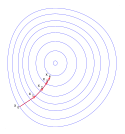
Gradientní sestup

Gradientní sestup (anglicky gradient descent) je iterativní optimalizační algoritmus prvního řádu pro nalezení lokálního minima diferencovatelné funkce. Myšlenkou metody je posouvat se z výchozího bodu po krocích vždy v opačném směru gradientu (nebo přibližného gradientu) funkce v daném bodě, protože to je směr nejstrmějšího klesání její hodnoty. Naopak krokování ve směru gradientu povede k lokálnímu maximu této funkce; postup je pak známý jako gradientní výstup.

Algoritmus se přičítá Cauchymu, který ho poprvé zmínil v roce 1847, ale jeho konvergenční vlastnosti pro nelineární optimalizační problémy byly poprvé studovány Haskellem Currym v roce 1944.

Gradientní sestup je spojitou analogií metody hill-climbing (gradientní algoritmus). Sám je základem dalších metod, zejména algoritmu zpětného šíření chyby používaného pro učení umělých neuronových sítí.

Popis

Gradientní sestup je založen na pozorování, že pokud je funkce více proměnných ${\displaystyle F(\mathbf {x} )}$ definována a diferencovatelná v sousedství bodu ${\displaystyle \mathbf {a} }$, pak ${\displaystyle F(\mathbf {x} )}$ klesá nejrychleji, pokud se jde z ${\displaystyle \mathbf {a} }$ ve směru záporného gradientu ${\displaystyle F}$ v ${\displaystyle \mathbf {a} ,-\nabla F(\mathbf {a} )}$ . Z toho vyplývá, že se v řadě iterací z ${\displaystyle \mathbf {a_{n}} }$ posuneme k nižší hodnotě funkce ${\displaystyle F(\mathbf {x} )}$ v bodě ${\displaystyle \mathbf {a_{n+1}} ,}$ pokud

${\displaystyle \mathbf {a} _{n+1}=\mathbf {a} _{n}-\gamma \nabla F(\mathbf {a} _{n})}$

pro ${\displaystyle \gamma \in \mathbb {R} _{+}}$ dost malé, aby platilo ${\displaystyle F(\mathbf {a_{n}} )\geq F(\mathbf {a_{n+1}} )}$. Jinými slovy člen ${\displaystyle \gamma \nabla F(\mathbf {a} )}$ odčítáme od ${\displaystyle \mathbf {a} }$, protože se chceme pohybovat proti nejstrmějšímu nárůstu směrem k lokálnímu minimu. Vyjděme tedy z libovolného (náhodně nebo záměrně zvoleného) bodu ${\displaystyle \mathbf {x} _{0}}$, v němž je ${\displaystyle F}$ definovaná a diferencovatelná, a zvažujme posloupnost ${\displaystyle \mathbf {x} _{0},\mathbf {x} _{1},\mathbf {x} _{2},\ldots }$ definovanou jako

${\displaystyle \mathbf {x} _{n+1}=\mathbf {x} _{n}-\gamma _{n}\nabla F(\mathbf {x} _{n}),\ n\geq 0.}$

Ta odpovídá monotónní posloupnosti

${\displaystyle F(\mathbf {x} _{0})\geq F(\mathbf {x} _{1})\geq F(\mathbf {x} _{2})\geq \cdots ,}$

takže lze doufat, že ${\displaystyle (\mathbf {x} _{n})}$ dokonverguje k nějakému lokálnímu minimu ${\displaystyle F}$ (pokud nebude divergovat k minus nekonečnu, což by znamenalo nalezení globálního infima ${\displaystyle F}$, anebo pokud se v některém kroku nedostaneme mimo oblast, kde je ${\displaystyle F}$ definovaná či „pěkná“). Všimněte si, že hodnota velikosti kroku ${\displaystyle \gamma }$ se může měnit při každé iteraci. S určitými předpoklady o funkci ${\displaystyle F}$ – například ${\displaystyle F}$ lokálně konvexní a ${\displaystyle \nabla F}$ lipschitzovská – a o algoritmu výběru ${\displaystyle \gamma }$ – např. Barzilaiovou-Borweinovou metodou^[1]

${\displaystyle \gamma _{n}={\frac {\left|\left(\mathbf {x} _{n}-\mathbf {x} _{n-1}\right)^{T}\left[\nabla F(\mathbf {x} _{n})-\nabla F(\mathbf {x} _{n-1})\right]\right|}{\left\|\nabla F(\mathbf {x} _{n})-\nabla F(\mathbf {x} _{n-1})\right\|^{2}}}}$

– lze zaručit konvergenci na lokální minimum. Pokud je funkce ${\displaystyle F}$ konvexní, lze zaručit nalezení globálního řešení.

Gradientní sestup funguje v prostorech libovolné dimenze, dokonce i v nekonečněrozměrných prostorech. V tom případě se obvykle prohledává nějaký prostor funkcí a počítá se Fréchetova derivace funkcionálu, který se má minimalizovat, aby se určil směr sestupu.^[2]

Reference

V tomto článku byl použit překlad textu z článku Gradient descent na anglické Wikipedii.

Externí odkazy

• Obrázky, zvuky či videa k tématu gradientní sestup na Wikimedia Commons