Heronův vzorec

Heronův vzorec je vzorec pro výpočet obsahu obecného trojúhelníku (v eukleidovské rovině) pomocí délek jeho stran.

Pokud 3 kladná čísla splňují trojúhelníkovou nerovnost, existuje v eukleidovské rovině (podle věty sss) až na polohu a orientaci jediný trojúhelník s těmito délkami stran. Takže je jednoznačně určen i jeho obsah a je tedy funkcí stran. Ta musí být obecně symetrická a kvadraticky homogenní a H. v. ukazuje, jak přesně vypadá.

Vzorec

Jsou-li ${\displaystyle a,b,c}$ délky stran trojúhelníka, platí pro jeho obsah

${\displaystyle S={\sqrt {s(s-a)(s-b)(s-c)}},}$

kde ${\displaystyle s={\frac {a+b+c}{2}}}$ je poloviční obvod trojúhelníku.

Důkaz

Heronův vzorec lze odvodit již na základní škole, spočívá na Pýthagorově větě.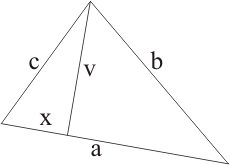

Označme x vzdálenost vrcholu B od paty kolmice z vrcholu A na stranu a (výšky). Pro pravoúhlý trojúhelník na obrázku platí:

${\displaystyle \ x^{2}+v^{2}=c^{2}}$

${\displaystyle \ (a-x)^{2}+v^{2}=b^{2}}$

Odečteme-li od druhé rovnice první, dostaneme:

${\displaystyle \ a^{2}-2ax=b^{2}-c^{2}}$

Z tohoto vztahu vyjádříme x:

${\displaystyle x={\frac {a^{2}+c^{2}-b^{2}}{2a}}}$

Toto platí i v pravoúhlém trojúhelníku, v tupoúhlém s opačným znaménkem. Jestliže za x dosadíme do první rovnice, získáme výšku v:

${\displaystyle \ v^{2}=c^{2}-x^{2}}$

${\displaystyle v^{2}=c^{2}-\left({\frac {a^{2}+c^{2}-b^{2}}{2a}}\right)^{2}}$

${\displaystyle v^{2}=c^{2}-{\frac {\left(a^{2}+c^{2}-b^{2}\right)^{2}}{4a^{2}}}}$

${\displaystyle v^{2}={\frac {4c^{2}a^{2}-\left(a^{2}+c^{2}-b^{2}\right)^{2}}{4a^{2}}}}$

${\displaystyle v={\frac {\sqrt {4c^{2}a^{2}-\left(a^{2}+c^{2}-b^{2}\right)^{2}}}{2a}}}$

Dosadíme-li tuto výšku do vzorce pro obsah trojúhelníku

${\displaystyle S={\frac {av}{2}},}$

dostaneme

${\displaystyle S={\frac {\sqrt {4c^{2}a^{2}-\left(a^{2}+c^{2}-b^{2}\right)^{2}}}{4}}}$

Dále pomocí rozkladů upravíme výraz pod odmocninou:

${\displaystyle S={\frac {\sqrt {\left(2ac+a^{2}+c^{2}-b^{2}\right)\left(2ac-a^{2}-c^{2}+b^{2}\right)}}{4}}}$

${\displaystyle S={\frac {\sqrt {\left[\left(a+c\right)^{2}-b^{2}\right]\left[b^{2}-\left(a-c\right)^{2}\right]}}{4}}}$

${\displaystyle S={\frac {\sqrt {\left(a+c+b\right)\left(a+c-b\right)\left(b+a-c\right)\left(b-a+c\right)}}{4}}}$

Dosadíme poloviční obvod s,

${\displaystyle \ a+b+c=2s}$

a dostáváme výsledný vzorec:

${\displaystyle S={\frac {\sqrt {2s\left(2s-2a\right)\left(2s-2b\right)\left(2s-2c\right)}}{4}}}$

${\displaystyle S={\frac {\sqrt {16s\left(s-a\right)\left(s-b\right)\left(s-c\right)}}{4}}}$

${\displaystyle S={\sqrt {s\left(s-a\right)\left(s-b\right)\left(s-c\right)}}}$

Historie

Vzorec byl formulován Hérónem z Alexandrie a důkaz byl publikován v jeho knize Métrika, napsané v první polovině 1. století.^[1]

Poznámky

Kratší důkaz je možný pomocí kosinové věty.

Díky trojúhelníkové nerovnosti jsou všechny činitele odmocněnce H. v. kladné.

Jedná se asi o nejsložitější matematický vzorec základní školy.

Heronův vzorec je limitním případem Brahmaguptova vzorce pro obsah tětivového čtyřúhelníku.

Reference

Související články

• Trojúhelník
• Obsah
• Tětivový čtyřúhelník

Externí odkazy

• Obrázky, zvuky či videa k tématu Heronův vzorec na Wikimedia Commons
• důkaz Heronova vzorce