Hra života

Hra života nebo také život (anglicky Game of Life či pouze Life) je dvoustavový, dvourozměrný celulární automat[1], který svým chováním připomíná vývoj společenství živých organismů.[2] Odehrává se na matici buněk, jejíž stav předurčuje podobu hry v následujícím kroku. Uživatel pouze určí výchozí konfiguraci a dále již hra běží automaticky podle předem daných pravidel. Čas je ve hře diskrétní[3], při každém uplatnění pravidel se posune o jednotku. Hra života se od podobných celulárních automatů liší v pravidlech pro zrod nových buněk a jejich přežití. Kořeny hry života sahají do roku 1940, kdy maďarský matematik John von Neumann přišel s konceptem celulárních automatů. Hru života jako takovou však vymyslel až britský matematik John Horton Conway v roce 1970. V průběhu hry vznikají různé tvary, které se dělí do kategorií jako jsou zátiší, oscilátory, děla a další. Hra života je příkladem systému, kde z jednoduchých pravidel vzniká komplexní chování - objevují se zde tzv. emergentní struktury.
Herní svět
Dvourozměrná hrací plocha Hry života se znázorňuje jako čtvercová síť. Její políčka se nazývají buňky (proto název celulární neboli buněčný automat)[4]. Každá buňka může nabývat dvou stavů, může být živá či mrtvá.[2] Buňka sousedí s dalšími buňkami, se kterými se dotýká hranou (ortogonálně) či vrcholem (diagonálně) a tvoří tak Moorovo okolí. [3] Nový stav buňky určuje přechodová funkce podle stavu této buňky a jejího okolí v předchozím kroku.[3] Stav všech buněk se mění naráz.[2] Celulární automaty, které po vzoru Hry života splňují výše uvedené skutečnosti tvoří třídu celulárních automatů založených na Hře života (Life-like cellular automata).[4] Sestavení živých a neživých buněk na hrací ploše se říká konfigurace nebo vzor.[1] Jednotkou času je ve Hře života generace.[3] Jedna generace představuje jedno provedení přechodové funkce.[3] Podle toho, jaká pravidla pro změnu stavu buněk přechodová funkce uplatňuje, se hovoří o konkrétním názvu life-like celulárního automatu.[4]
Pravidla
Popis
Jako Hra života se označuje celulární automat jehož přechodová funkce používá množinu pravidel, kterou na počátku 70. let definoval britský matematik John Conway takto[5]:
- Každá živá buňka s méně než dvěma živými sousedy zemře.
- Každá živá buňka se dvěma nebo třemi živými sousedy zůstává žít.
- Každá živá buňka s více než třemi živými sousedy zemře.
- Každá mrtvá buňka s právě třemi živými sousedy oživne.
Tato konkrétní pravidla jsou označována jako S23/B3.[4] Čísla před lomítkem říkají kolik sousedů musí buňka mít, aby přežila, čísla za lomítkem říkají kolik sousedů potřebuje mrtvá buňka k ožití. Písmena jsou zkratky anglických výrazů to survive a to be born. Tato pravidla byla vybrána vědomě s cílem zajistit, aby populace živých buněk rostla nepředvídatelně.[5]
Konkrétně jde o splnění požadavků, že by:
- neměl existovat žádný počáteční vzor, pro který by šlo snadno dokázat, že populace může růst nade všechny meze[5],
- měly existovat počáteční vzory zdánlivě nade všechny meze rostoucí[5]
- a že by měl existovat takový počáteční vzor, který se určitou dobu vyvíjí než úplně vymizí, přejde do stabilní podoby anebo do oscilační fáze.[5]
Možných pravidel pro Life-like buněčné automaty je celkem 2^18.[3] Pro definici počtu buněk nutných k přežití či oživnutí lze totiž použít pro každou z nich celkem 9 možností (0-8 sousedů) a buňka se nachází ve dvou stavech. Při některých pravidlech všechny vzory vymizí, v některých dochází k explozivnímu růstu.[3]
Příklad
Obrázek znázorňuje vývoj vzoru v průběhu tří generací. Černě vybarvená buňka je ve stavu živém, bílá ve stavu neživém. Číslo uvnitř buňky označuje počet živých buněk v jejich okolí. Přechodová funkce se řídí pravidly S23/B3.
V nulté generaci se vlevo dole nachází živá buňka s právě jedním sousedem. Tato buňka po aplikaci pravidel zemře a v příští generaci se stane neživou. Vlevo a vpravo se nachází živé buňky se dvěma sousedy. Tyto buňky přežijí do příští generace. Čtyři neživé buňky uprostřed, které mají každá tři živé sousedy, v příští generaci ožijí. V první generaci se uprostřed nachází čtyři buňky každá se čtyřmi sousedy. Tyto buňky podle pravidel zemřou a v příštím kole budou neživé. Pravidla se uplatní i na ostatní buňky a výsledkem je generace 2. V tomto případě je druhá generace stejná jako nultá. Tento tvar spadá do skupiny oscilátorů s periodou dvě generace. Vzor se nazývá ropucha (toad).
Původ

Celulární automat vytvořil v roce 1940 John von Neumann za pomoci Stanislava Ulama ve snaze vytvořit sebereprodukující se stroj, tedy stroj schopný vytvářet své vlastní kopie.[6] Neumanův celulární automat měl podobu dvojrozměrné mřížky, kde se každá buňka mohla nacházet v jednom z 29 stavů.[3] Po čase zájem o celulární automaty trochu opadl, kvůli nedostatečnému výkonu tehdejší výpočetní techniky.[6] Novou vlnu zájmu o celulární automaty přinesla až Hra života na počátku sedmdesátých let.[6]
Hra života se na veřejnosti poprvé objevila v říjnu roku 1970 jako článek v rubrice Matematické hry spravované Martinem Gardnerem v časopise Scientific American. [5] Jejímu představení následoval dva roky trvající mezinárodní rozruch.[4] Martin Gardner přiznal, že její publikování způsobilo bezprecedentní čtenářský ohlas a že brzy bude potřeba vydat další článek ohledně technických principů, na který je Hra života založena.[3] Protože časopis Scientific American neposkytoval příznivcům Hry života dostatečný prostor pro publikaci nových objevů, založil Robert T. Wainwright v roce 1971 vlastní časopis s názvem LifeLine.[3] Časopis vycházel čtvrtletně a až do jeho ukončení v roce 1973 (kvůli osobním důvodům vydavatele) se těšil velkému zájmu čtenářů - zpočátku si jej předplácelo asi 150 zájemců, ke konci kolem 1000.[3]
Počáteční výzkum Hry života provázely dvě zásadní otázky.[3] Obě položil Conway. První z nich se objevila již v Gardnerově prvotním článku z října roku 1970.[5] Šlo o to zjistit, zda nějaký tvar může růst bez omezení. Jinými slovy, zda nějaká konfigurace s konečným počtem živých buněk může růst nad určitý konečný horní limit. Conway předpokládal, že taková konfigurace neexistuje a slíbil odměnu 50 dolarů tomu, kdo do konce roku jeho domněnku potvrdí či vyvrátí. Článek obsahoval i několik konceptuálních způsobů, jak Conwayův předpoklad vyvrátit. Jedním způsobem je najít takovou konfiguraci, která opakovaně vytváří pohybující se vzory. V článku je taková konfigurace označena jako dělo (gun). Dalším způsobem je vytvořit takovou konfiguraci, která se hýbe sama a zanechává za sebou stopu. Tato konfigurace je v článku označena jako kouřící vlak (puffer train). Cenu vyhrál R. William Gosper, když v listopadu téhož roku představil funkční dělo podle Conwayova popisu.[4] Po svém autorovi nese vzor název Gosperovo dělo na kluzáky (Gosper Glider Gun). Gosper později vyřešil problém i druhou metodou, když zkonstruoval první kouřící vlak (puffer train)[3].
Druhou zásadní otázku položil Conway v časopise Lifeline roku 1972.[3] Této otázce se také říká problém existence dědečka (The Grandfather Problem)[3] a Conway za její zodpovězení vypsal odměnu dalších 50 dolarů. Jde o to zjistit, jestli existuje taková konfigurace, která se vyskytuje pouze v druhé a už v žádné další generaci. Tato otázka nebyla dodnes zodpovězena.[zdroj?]
Mezi další dosud nevyřešené problémy patří dokázat, že existují vzory se všemi periodami (periody 19, 23, 34, 38, 41, 43 a 53 nejsou známé)[zdroj?], najít takový vzor, který vytváří více kopií sebe samého[zdroj?] a dokázat existenci zátiší, které mohou vzniknout pouze v nulté generaci[zdroj?].
Přehled tvarů
Vzory, které ve Hře života vznikají lze rozdělit do deseti hlavních kategorií. [7] Nadpis tvoří český překlad a anglický ekvivalent. U každé kategorie je jako příklad uvedeno několik často uváděných tvarů.
Zátiší (Still life)
Jako stabilní konfigurace se označuje vzor, který je svým vlastním rodičem.[1] Jako rodič vzoru se označuje přímý předchůdce.
Zátiší někdy označované také jako invariantní podoby (invariant forms)[4] je skupina tvarů, které se v průběhu hry nemění.[3] Jedná se o stabilní vzory složené z konečného počtu živých buněk.[1] Pro určování počtu zátiší o určitém množství živých buněk se používá užší definice, která přidává podmínku, že zátiší nesmí být možné rozdělit způsobem při kterém by jeho části zůstaly stabilní samostatně.[1] Vzory, které vyhovují první ale už ne druhé definici se nazývají pseudozátiší (pseudo still lifes).[1] Příkladem pseudozátiší je dvojblok na obrázku níže.
 | 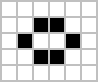 |  |  |  |
| Blok (Block) | Včelín (Beehive) | Bochník (Loaf) | Loď (Boat) | Dvojblok (bi-block) |
Oscilátory (Oscillators)
Oscilátor je nestabilní konečný vzor, který je svým vlastním předchůdcem.[1] Předchůdcem se myslí jakýkoliv vzor, z něhož se daný vzor vyvinul za určitý počet generací.[1] Oscilátory periodicky přecházejí mezi konstantním počtem konfigurací.[4] U oscilátorů se sleduje periodicita. Oscilátory s periodou 2 postupně nabývají podoby jedné ze dvou možných konfigurací[4] a říká se jim alternátory.[3] První tři oscilátory na obrázcích mají periodu 2, pulzar má periodu 3.
 |  |  | |
| Blikač (Blinker) | Ropucha (Toad) | Maják (Beacon) | Pulzar (Pulsar) |
Děla
Dělo (anglicky gun) je stacionární vzor, který neustále vytváří hvězdné lodi nebo vidle (anglicky rakes).[1] Příkladem je kluzákové dělo, které každých třicet generací vypustí kluzák.[4]
Hvězdné lodě
Hvězdná loď (anglicky starship) je pohybující se vzor, který se v nezměněné podobě znovu objevuje po určitém počtu generací.[1] V nekonečném prostoru hry života není vzor nikdy periodický.[3] U hvězdných lodí se sleduje jejich rychlost, která je udávána jako zlomek „rychlosti světla“ c.[1] Rychlost světla je definována jako jedna buňka za generaci a představuje největší rychlost, jakou se může ve Hře života objekt pohybovat.[1]
Nejznámějším případem hvězdné lodi je kluzák.[1] Jedná se o vzor složený z pěti živých buněk, který se po čtyřech fázích posune o jednu buňku v diagonálním směru[3] (tj. rychlostí c/4).[1]
 |  |
| Kluzák (Glider) | Lehká hvězdná loď (LWSS) |
Kuřáci (Puffers)
Kuřák je vzor, který se pohybuje jako hvězdná loď (starship) s tím, že za sebou nechává stopu.[1] První puffer objevil Bill Gosper v roce 1971.[3] Tento vzor se pohyboval rychlostí c/2 ortogonálně.[1] Obrázek ukazuje dva kuřáky. Nahoře je zobrazen Gosperův kouřící vlak, dole vzor nazývaný Blinker Puffer 1, jehož objevil Robert Wainwright v roce 1984.
Rajská zahrada (Garden of Eden)
Rajská zahrada nebo také sirotek (orphan) je taková konfigurace, která se může objevit pouze v nulté generaci.[1] O jejich existenci se vědělo dlouho před jejich praktickou realizací ve Hře života. Existencí této konfigurace se na počátku šedesátých let předpověděli Edward F. Moore a John Myhill.[4]
Moorův-Myrhillův teorém říká: pokud má nějaká konfigurace více než jednoho předka, tak existuje taková konfigurace, která žádného předka nemá a naopak.[4] Teorém se vysvětluje na následujícím příkladu.[4] Pokud se hrací plocha skládá z konečného množství buněk N a každá buňka se může nacházet ve dvou stavech, potom celkový počet možných konfigurací je 2^N v každé generaci. Pakliže jsou dvě různé konfigurace vytvoří v další generaci totožnou konfiguraci, pak přechodovou funkcí bylo vygenerováno pouze 2^N - 1 konfigurací a jedna konfigurace tedy nemá předchůdce.
První praktický vzor nalezl Roger Banks v roce 1971.[1] Tento vzor je na obrázku níže.
Metuzalémové (Methuselahs)
Jakýkoliv malý vzor, jehož stabilizace trvá dlouhou dobu.[1] R-pentomino se stabilizuje až po 1103 generacích, žalud po 5206 generacích a králíkům přechod do stabilního stavu trvá 17332 generací.
 |  |  |
| R-pentomino | Žalud (Acorn) | Králíci (Rabbits) |
Agary (Agars)
Agar je takový vzor, který pokrývá celou hrací plochu a je periodický jak v prostoru tak čase.[1]
 |  |
| Benátské rolety (Venetian blinds) | Chickenwire |
Pilové zuby (Sawtooths)

Konečný vzor, jehož populace roste bez omezení ale neroste do nekonečna přímo. Vždy po určité době růstu klesne na určitou konstantní hodnotu.[1]
První vzor, jehož graf populace v průběhu generací připomínal stále rostoucí zuby pily sestrojil Dean Hickerson v roce 1991.[7]
Knoty (Wicks)
Vzor, jehož tvoří dlouhá šňůra opakujících se vzorů složená ze zátiší nebo oscilátorů, která na jedné straně může být zapálena a uhořívat.[1] Zápalná šňůra (Fuse) je zvláštní druh knotu, který hoří vždy.[7] Ukazuje ji následující obrázek.
Pravidla celulárních automatů založených na Hře života
Life-like celulární automaty se rozlišují podle pravidel, která uplatňuje přechodová funkce. Existuje množství jiných pravidel než je původní S23/B3 tvořící Hru života. Tato pravidla tvoří další zajímavé tvary. První číslo před lomítkem je počet okolních buněk potřebných k přežití již živé buňce, druhé počet buněk na zrod. Pokud první číslo chybí, buňka vždy umře. Některá z těchto pravidel shrnuje následující tabulka.
| Pravidlo | Jméno | Popis |
|---|---|---|
| /2 | Semena | Chaotický vznik |
| /234 | Ubrousky | Krajkovité vzory |
| 012345678/3 | Vločky, nesmrtelné | Vločkovité vzory |
| 1/1 | Suky | |
| 12345/3 | Bludiště | Tvoří vzhled jako bludiště |
| 125/36 | 2x2 | Pokud je vzor složen z bloků 2×2, pokračuje ve vývoji stejnou formou. Má hodně oscilátorů a lodí |
| 1357/1357 | Nahrazovač | Nahrazovač Edwarda Fredkina: každý vzor je jednou nahrazen několikanásobnými kopiemi sebe sama |
| 1358/357 | Améba | Dobře vyvážený poměr mezi životem a smrtí; tvoří tvary s chaotickými vnitřky a rychle pohybujícími hranicemi. Její lodě[nedostupný zdroj] |
| 23/3 | Game of Life | Velmi komplexní chování |
| 23/36 | HighLife | Podobný Game of Life |
| 2345/45678 | Města za zdmi | Tvoří oblasti s pevnými hranicemi, pohyb je pouze uvnitř |
| 235678/3678 | Skvrny | Vzor se rychle stabilizuje, poté už jen slabě osciluje |
| 235678/378 | Srážlivý | Vzor má sklon se rozvíjet právě opačně než velmi podobné pravidlo Skvrn |
| 238/357 | Pseudo life | Vývoj vzoru je podobný Game of Life, ale málo vzorů z Life funguje s tímto pravidlem |
| 245/368 | Pohyb | Náhodné vzory mají sklon se stabilizovat, ale má mnoho přirozeně vyvinutých a navrhovaných lodí |
| 34/34 | 34 Life | Vytvořena původně jako stabilní alternativa pro Life, dokud počítačové simulace neukázaly, že velké vzory mají sklon explodovat. Má hodně malých oscilátorů[nedostupný zdroj] a lodí |
| 34678/3678 | Day & Night | Symetricky obrácený. Má navržené vzory s velmi komplexním chováním |
| 4567/345 | Přizpůsobení | Tvoří trvalé kosočtvercové vzory s částečně vyplněným vnitřkem |
| 45678/3 | Korál | Vzory připomínají pomalu se tvořící korálové textury |
| 5/345 | Long life | Zkoumána Andrewem Trevorrowem, má oscilátory s velmi dlouhou periodou |
| 5678/35678 | Kosoaméba | Formuje se do velkých kosočtvercových tvarů s chaoticky oscilujícími hranicemi. |
Příklad algoritmu
n=100; % počet řádků a sloupců
t=100; % čas
U=rand(n); % matice s náhodnými elementy
p=0.25; % počáteční poměr
A=(U<p); % počáteční matice se kterou se hraje
B=zeros(n); % pomocná matice, kam zapisuji další iterační stavy
for i=1:t
for x=2:n-1
for y=2:n-1
okoli=A(x-1,y-1)+A(x-1,y)+A(x-1,y+1)+A(x,y-1)+A(x,y+1)+A(x+1,y-1)+A(x+1,y)+A(x+1,y+1);
if A(x,y)==1 % živá buňka
if okoli==2 | okoli==3
B(x,y)=1; % zůstane
else
B(x,y)=0; % zahyne
end
else % mrtvá buňka
if okoli==3
B(x,y)=1; % ožije
else
B(x,y)=0; % neožije
end
end
end
end
imshow(B)
pause(.01)
A=B; % před dalším krokem je nutno matici A aktualizovat
end
Reference
- ↑ a b c d e f g h i j k l m n o p q r s t u v SILVER, Steven. Life Lexicon [online]. 28.2.2006 [cit. 2011-01-25]. Dostupné v archivu pořízeném dne 26-05-2013. (anglicky)
- ↑ a b c GARDNER, Martin. Mathematical Games: The fantastic combinations of John Conway.. Scientific American. 1970, čís. 223, s. 120–123. [<http://www.fpga-faq.org/sb-metal_hold/CD_08/lifepatt.pdf> Dostupné online]. (anglicky)[nedostupný zdroj]
- ↑ a b c d e f g h i j k l m n o p q r s t ADAMATZKY, Andrew. Game of Life Cellular Automata. London: Springer-Verlag, 2010. 573 s. ISBN 978-1-84996-216-2. (anglicky)
- ↑ a b c d e f g h i j k l m SCHIFF, Joel L. Cellular automata: A Discrete View of The World. New Jersey: John Wiley & Sons, Inc, 2008. 252 s. Dostupné online. ISBN 978-0-470-16879-0. (anglicky)
- ↑ a b c d e f g BERLEKAMP, Elwyn R.; CONWAY, John H.; GUY, Richard K. Winning Ways for Your Mathematical Plays. Wellesley: A K Peters, 2004. 967 s. ISBN 1-56881-144-6. (anglicky)
- ↑ a b c HUSÁKOVÁ, Martina. Celulární automaty: Znalostní technologie III materiál pro podporu studia. [s.l.]: [s.n.], 2007. 14 s.
- ↑ a b c Life Wiki [online]. [cit. 2011-01-25]. Dostupné online. (anglicky)
Online ukázka - applet
- http://www.andrewlowndes.co.uk/blog/graphics/conways-game-of-life-in-webgl Archivováno 24. 3. 2014 na Wayback Machine.
Související články
Externí odkazy
 Obrázky, zvuky či videa k tématu Hra života na Wikimedia Commons
Obrázky, zvuky či videa k tématu Hra života na Wikimedia Commons - (česky) Český Java applet pro online simulace
- (slovensky) Slovenské prostředí pro spouštění simulací online[nedostupný zdroj]
- (anglicky) Prostředí pro spouštění simulací online
- (anglicky) Diskusní fórum zaměřené na Hru života
- (anglicky) Rozcestník na čísla časopisu Lifeline
- (anglicky) Conway's game of life implementation. (Silverlight)
- (anglicky) Game of Life on JavaScript
Média použitá na této stránce
Autor: "Thane Plambeck", Licence: CC BY 2.0
"John H. Conway at conference on Combinatorial Game Theory at Banff International Research Station, June, 2005"
Kluzák ze Hry života.
Diagram from the Game of Life
Oscilátor žába ze Hry života.
Game of life: loaf
Oscilátor maják ze Hry života.
Game of life: block
Lehká hvězdá loď ze Hry života.
Game of life: beehive
Oscilátor pulzar ze Hry života.
Autor: Simpsons contributor, Licence: CC0
Graf znázorňuje počet živých buněk v průběhu 9620 generací.
Autor: Lucas Vieira, Licence: CC BY-SA 3.0
Bill Gosper's Glider Gun in action—a variation of Conway's Game of Life. This image was made by using Life32 v2.15 beta, by Johan G. Bontes.
Blikač
























