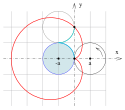
Kardioida

Vznik srdcovky kotálením

Srdcovka a parabola navzájem zobrazené kruhovou inverzí

Kardioida (z řeckého καρδία – srdce) neboli srdcovka je algebraická rovinná křivka 4. stupně (kvartika). Patří mezi kotálnice (cykloidy) a lze ji sestrojit jako trasu pevně daného bodu kružnice, která se kotálí kolem kružnice o stejném poloměru. Zároveň patří mezi konchoidy a lze ji konstruovat tak, že se na kružnici zvolí bod a na všech sečnách procházejících tímto bodem se vezmou body vzdálené od druhého průsečíku právě o poloměr řečené kružnice. Také ji lze získat jako obraz paraboly při kruhové inverzi.

Pojmenoval ji v roce 1741 italský matematik Giovanni Salvemini.

Srdcovka je součástí obrazce ve fraktálu Mandelbrotovy množiny.

Rovnice

Kardioida v kartézském souřadnicovém systému s vyznačenými konstrukčními kružnicemi

Kardioidu lze popsat následujícím parametrickým vyjádřením v kartézských souřadnicích (a je poloměr kružnic při kotálení, počátek je v středu nehybné kružnice):

${\displaystyle x=a(2\cos t-\cos 2t-1),\,}$

${\displaystyle y=a(2\sin t-\sin 2t).\,}$

V komplexní rovině tomu odpovídá parametrizace

${\displaystyle z=a(2e^{it}-e^{2it}).\,}$

Příslušná obecná rovnice v kartézských souřadnicích je

${\displaystyle (x^{2}+y^{2}-a^{2})^{2}-4a^{2}((x-a)^{2}+y^{2})=0,}$

respektive v komplexní rovině

${\displaystyle (z{\bar {z}}-a^{2})^{2}-4a^{2}(z-a)({\bar {z}}-a)=0}$.

Další možností je zápis v polárních souřadnicích:

${\displaystyle r=2a(1-\cos \theta ).}$

Míry

Délka srdcovky je rovna

${\displaystyle l=16a}$

a obsah její vnitřní oblasti

${\displaystyle S=6\pi a^{2}}$.

Reference

V tomto článku byl použit překlad textu z článku Cardioid na anglické Wikipedii.

Externí odkazy

• Obrázky, zvuky či videa k tématu kardioida na Wikimedia Commons
• Encyklopedické heslo Kardioida v Ottově slovníku naučném ve Wikizdrojích
• Slovníkové heslo kardioida ve Wikislovníku
• Kardioida v encyklopedii MathWorld (anglicky)