Kombinační číslo


Kombinační číslo je matematická funkce, která udává počet kombinací, tzn. způsobů, jak vybrat -prvkovou podmnožinu (bez ohledu na pořadí jejích prvků) z -prvkové množiny ( a jsou čísla přirozená). Kombinační čísla zapisujeme (čte se „n nad k“), někdy se používá také značení , či . Hodnotu kombinačních čísel lze vyjádřit pomocí faktoriálu:
Platí rovnost
Kombinační čísla se používají hlavně v kombinatorice, velice důležité je využití v binomické větě (přičemž je zde označováno jako binomický koeficient), v Leibnizově pravidle nebo při výpočtu pravděpodobnosti v binomickém rozdělení.
Základní vlastnosti
Pro přirozená čísla n a k, kde a , platí:[1]
Zobecnění kombinačních čísel
Pokud definujeme kombinační číslo takto
,
kde je nezáporné celé číslo, pak je zřejmé, že pravá strana má smysl, i když číslo není celé nezáporné. Na číslo dokonce nemusíme klást žádné podmínky, může se jednat dokonce o číslo komplexní. Vztah je tedy přirozeným zobecněním kombinačních čísel a je používán hlavně v zobecněné binomické větě.
Další možnou definici nám umožňuje nahrazení faktoriálu gama funkcí
,
kde i mohou být komplexní čísla – pak ovšem nebudou platit popsané vlastnosti kombinačních čísel pro všechny hodnoty.
Odkazy
Literatura
- MATOUŠEK, Jiří; NEŠETŘIL, Jaroslav. Kapitoly z diskrétní matematiky. 3., upravené a doplněné vyd. Praha: Karolinum, 2007. ISBN 978-80-246-1411-3. Kapitola 3. Kombinatorické počítání, s. 76–82.
- BARTSCH, Hans-Jochen. Matematické vzorce. 4., upravené vyd. Praha: Academia, 2006. ISBN 80-200-1448-9. Kapitola 1.7.1. Binomické koeficienty, binomická věta, s. 156–160.
Reference
- ↑ HAVRLANT, Lukáš. Kombinace. www.matweb.cz [online]. [cit. 2025-02-20]. Dostupné online.
Související články
- Pascalův trojúhelník
- Binomická věta
- Pravidlo součtu
- Kombinatorika
- Variace – na rozdíl od kombinace, u variace záleží na pořadí vybraných prvků.
Externí odkazy
 Obrázky, zvuky či videa k tématu kombinační číslo na Wikimedia Commons
Obrázky, zvuky či videa k tématu kombinační číslo na Wikimedia Commons - Kombinační číslo na encyklopedii MathWorld (anglicky)
- Kalkulátor kombinačního čísla
Média použitá na této stránce
Autor: User:Conrad.Irwin originally User:Drini, Licence: CC BY-SA 3.0
Pascal's triangle to 5 rows, the first row is the zero row. It also called the Halayudha's triangle, in honor of the Sanskrit prosody scholar who described it. (See: Alexander Zawaira and Gavin Hitchcock (2008), A Primer for Mathematics Competitions, Oxford University Press, ISBN 978-0-19-156170-2, page 237)
Autor: Cmglee, Licence: CC BY-SA 3.0
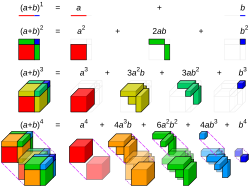
Visualisation of binomial expansion up to the 4th power.