Kružnice devíti bodů

Kružnice devíti bodů se nazývá taková kružnice trojúhelníka, na níž leží jeho následující body:
- středy stran
- paty výšek
- středy spojnic vrcholů s ortocentrem (ortocentrum = společný bod výšek trojúhelníka)
Kružnice devíti bodů se nazývá též Feuerbachova kružnice, protože německý matematik Karl Wilhelm Feuerbach byl prvním, kdo dokázal, že se kružnice devíti bodů dotýká kružnice vepsané a kružnic připsaných.
Kružnice devíti bodů je stejnolehlým obrazem kružnice opsané se středem stejnolehlosti v těžišti trojúhelníka a koeficientem κ = - 0,5. Z toho plyne, že její střed leží na Eulerově přímce ve středu úsečky, spojující ortocentrum se středem kružnice opsané. Její poloměr je polovinou poloměru kružnice opsané.
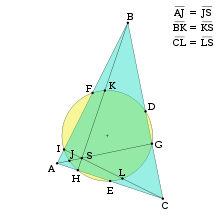
Shermanova úsečka
Pro každou stranu trojúhelníka platí následující:
- Konce stran leží na kružnici opsané.
- Strany se dotýkají kružnice vepsané.
- Středy stran leží na kružnici devíti bodů.
Matematik Sherman dokázal, že lze nalézt ještě jednu úsečku (tzv. „čtvrtou stranu“ trojúhelníka), která splňuje všechny tři výše uvedené podmínky.
Související články
Externí odkazy
 Obrázky, zvuky či videa k tématu Kružnice devíti bodů na Wikimedia Commons
Obrázky, zvuky či videa k tématu Kružnice devíti bodů na Wikimedia Commons - https://www.desmos.com/... - Interactive Sherman Line
Média použitá na této stránce
Circunferencias tangentes a la circunferencia de Feuerbach

