MOA (úhlová jednotka)

MOA, zkratka z anglického Minute Of Angle, česky úhlová minuta, což je šedesátina úhlového stupně. ^{[1] [2]}

Stupně, minuty a vteřiny

Při měření úhlů ve stupních se celý kruh dělí na 360 stupňů, což se značí jako 360°. Každý stupeň se dělí dále na 60 (úhlových) minut.

• 1° = 60′

Pro úhlové minuty se používá také označení arcmin nebo MOA.

Úhlová minuta se dělí na 60 (úhlových) vteřin.

• 1′ = 60′′

Pro úhlové vteřiny se používá také označení arcsec.

Vztah úhlu, vzdálenosti a velikosti.

Princip a oblasti použití

Předností úhlových jednotek, a tedy i MOA, je to, že odpovídají perspektivě zraku. Vzdálenější objekty jsou zdánlivě menší. Velikost objektu je tak úhlovou jednotkou udána ve vztahu k jeho vzdálenosti. Jinak řečeno, úhlová jednotka neudává velikost pozorovaného objektu, ale poměr velikosti ke vzdálenosti od pozorovatele.

Výpočet skutečné velikosti objektu (délky úsečky) vzdáleného 100m, který se jeví pozorovateli jako 1 MOA:

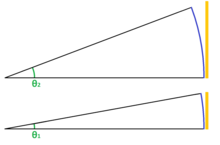
Výpočet je proveden pomocí standardních goniometrických funkcí. Na obrázku je úhel alfa (v našem případě 1 MOA) pozorovacím úhlem úsečky, která tvoří nejkratší stranu trojúhelníku protilehlou úhlu alfa. Délku strany, protilehlé k úhlu alfa, lze spočítat pomocí funkce sinus. Přepona trojúhelníku je poloměrem kružnice na obrázku. V našem případě 100 metrů.

Délka protilehlé strany = poloměr kružnice x sinus úhlu alfa

Délka protilehlé strany [m] = 100 [m] * sin(1/60)

Délka protilehlé strany = 0.02908882 [m]

Pozorovací úhel (na obr. zeleně), délka oblouku (modře), pozorovaný objekt (oranžová)

Při malém úhlu alfa platí, že velikost objektu (délka nejkratší strany) je téměř rovna délce oblouku na kružnici. Výšku objektu můžeme tedy počítat jako délku kružnice dělenou počtem jednotek. Poloměr kruhu představuje vzdálenost pozorovaného objektu.

Kruh má 360 stupňů a každý z nich má 60 MOA.

${\displaystyle 360*60=21600}$ (MOA celého kruhu)

Obvod kruhu

${\displaystyle o=2\pi r\,}$

Obvod kruhu o poloměru 100 m (zaokrouhledno na 1 desetinné místo):

${\displaystyle 2*3,14159*100m=628,3[m],}$

Obvod kruhu podělíme počtem MOA v kruhu (výsledek zaokrouhlen na 4 desetinná místa):

${\displaystyle {\frac {628,3}{21600}}=0,0291}$

Dosadili jsme poloměr v metrech, takže výsledek je také v metrech. Převedeno na mm dává hodnotu 1 MOA ve vzdálenosti 100 m zaokrouhledně 29,1 mm. ^[3]

Výhodou práce s úhlovou jednotkou je přímá úměra mezi vzdáleností a délkou. To znamená, že 1 MOA ve vzdálenosti 200 m je 2 x 29,1 mm, tedy 58,2 mm. Ve výpočtu je použita již zaokrouhledná hodnota spočtená pro kruh 100 m. Viz obrázek: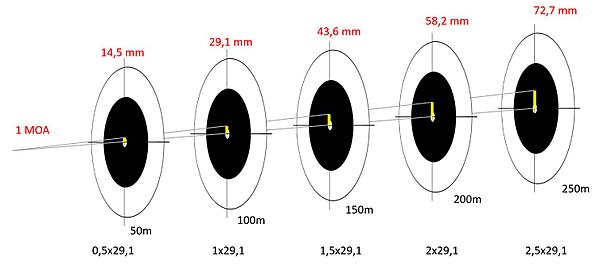

Zbraně

MOA se používá pro udávání přesnosti, respektive rozptylu zbraní. Například u služební zbraně se požaduje nepřesnost (rozptyl) do 1 MOA.^[3]

Dále se jednotka MOA používá v oblasti zaměřovací optiky. Například u kolimátorů udávají někteří výrobci velikost tečky na stínítku v MOA. Lze tak spočítat jak velkou část terče tato tečka zakryje na terči v konkrétní vzdálenosti.

Jiným příkladem je záměrná osnova nebo krok korekčních mechanismů puškohledů. Pokud střílíme na vzdálenosti 100 m a střely jsou vychýlené o 29,1 mm, potom je potřeba provést korekci na mechanismu puškohledu o 1 MOA. Při jiné vzdálenosti nebo odchylce je možno potřebnou korekci dopočítat jednoduchými matematickými úkony.

Další oblasti použití

MOA i další úhlové jednotky se používají například v astronomii, kartografii, geodézii ale i jiných oborech.

Odkazy

Reference

Externí odkazy

• YouTube:Understanding Minute of Angle (MOA) - Long Range Shooting Technique (anglicky)

Související články

• Prostorový úhel
• Mířidla
• Kolimátor
• Puškohled
• MilDot, Miliradián