Matematické kyvadlo

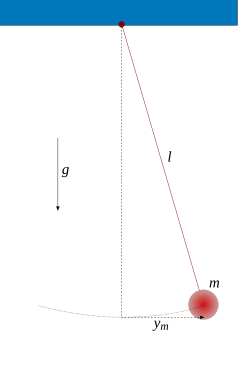
Matematické kyvadlo je nejjednodušším matematickým modelem kyvadla. Matematické kyvadlo je hmotný bod zavěšený na tenkém nepružném dokonale ohebném vlákně zanedbatelné hmotnosti, zanedbává se odpor vzduchu při pohybu kyvadla i tření v závěsu a tíhové pole se považuje za homogenní. Pohyb se navíc děje v jedné rovině a lze jej tak popsat jednou souřadnicí, většinou úhlem výchylky z rovnovážné polohy. Matematické kyvadlo je netlumený mechanický oscilátor, tedy soustava, která po dodání počáteční energie periodicky kmitá. Je to nelineární systém, ale při malých výchylkách (±5°) je průběh tohoto kmitání přibližně harmonický, lze jej tedy vyjádřit např. pomocí funkce sinus.

Na hmotný bod působí jen tíhová síla a tahová síla vlákna, která ho udržuje stále ve stejné vzdálenosti od závěsu. Tečná složka síly je

${\displaystyle F_{t}=mg\sin \varphi }$,

kde ${\displaystyle g}$ je tíhové zrychlení a φ je úhel, o který je vlákno vychýleno z rovnovážné polohy.

Pro tečné zrychlení platí:

${\displaystyle a_{t}=v'(t)=(l\omega )'=l\varphi ''(t).}$

Diferenciální rovnice pohybu kyvadla je z 2. Newtonova pohybového zákona tedy

${\displaystyle {\ddot {\varphi }}=-{\frac {g}{l}}\sin \varphi }$, což je Cayuchy-Eulerova diferenciální rovnice, a kde

kde ${\displaystyle l}$ je délka vlákna. Pokud je maximální výchylka z rovnovážné polohy ${\displaystyle \varphi _{\rm {max}}}$ malá (viz přesné řešení dále), lze funkci sinus nahradit lineární funkcí - přímo úhlem (v obloukové míře)

${\displaystyle \sin \varphi \approx \varphi }$.

Diferenciální rovnice má proto podstatně jednodušší tvar (lineární homogenní 2. řádu)

${\displaystyle {\ddot {\varphi }}+{\frac {g}{l}}\varphi =0.}$

Tato rovnice má partikulární řešení pro počáteční úhlovou výchylku ${\displaystyle \varphi _{m}}$ (jejíž velikost je amplitudou) a nulovou počáteční rychlost

${\displaystyle \varphi (t)=\varphi _{m}\cos \left({\sqrt {\frac {g}{l}}}\cdot t\right)}$,

kde ${\displaystyle t}$ je čas, což je pohybová rovnice lineárního harmonického oscilátoru s kruhovou frekvencí ω a periodou T

${\displaystyle \omega ={\sqrt {\frac {g}{l}}},T=2\pi {\sqrt {\frac {l}{g}}}}$.

Je vidět, že periodu ovlivňuje pouze délka kyvadla a (místní) tíhové zrychlení, hmotnost závaží na ni samozřejmě nemá vliv. Matematické kyvadlo lze tedy použít k měření místního tíhového zrychlení.

Neuvažujeme-li pouze malé výchylky kyvadla jako v předchozím případě, je mnohem náročnější pohybovou diferenciální rovnici vyřešit. K jejímu řešení je potřeba vyšší transcendentní funkce úplný eliptický integrál I. druhu

${\displaystyle K(k)=\int _{0}^{\pi /2}{1 \over {\sqrt {1-k^{2}\sin ^{2}{u}}}}\,du\,}$

pomocí nějž lze vyjádřit přesný vzorec pro periodu v závislosti na úhlovém rozkmitu ${\displaystyle \varphi _{m}\in (0;{\frac {\pi }{2}}\rangle }$

${\displaystyle T(\varphi _{m})=4{\sqrt {\ell \over g}}\,K\left(\sin {\varphi _{m} \over 2}\right).}$

Kyvadlo už v tomto případě není harmonický oscilátor. Periodu kmitání kyvadla lze vyjádřit pomocí řady

${\displaystyle T=2\pi {\sqrt {\frac {l}{g}}}\left(1+\left({\frac {1}{2}}\right)^{2}\sin ^{2}\left({\frac {\varphi _{m}}{2}}\right)+\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}\sin ^{4}\left({\frac {\varphi _{m}}{2}}\right)+...\right)}$.

Pokud uvažujeme nenulové tření při pohybu kyvadla přímo úměrné rychlosti, klesá maximální výchylka při kmitání exponenciálně v závislosti na čase.

Délka ${\displaystyle l}$ matematického kyvadla, které se kývá stejně (tzn. má stejnou periodu) jako fyzické kyvadlo, se nazývá redukovaná délka fyzického kyvadla. Mají-li být periody stejné pak platí

${\displaystyle l^{\star }={\frac {J}{ml}}}$,

kde ${\displaystyle l^{\star }}$ představuje redukovanou délku kyvadla, ${\displaystyle m}$ je hmotnost tělesa, ${\displaystyle l}$ je vzdálenost závěsu od těžiště a ${\displaystyle J}$ je moment setrvačnosti tělesa vzhledem k ose rotace.

Pokud naneseme na přímku, která je kolmá k ose otáčení ${\displaystyle O}$ a současně prochází těžištěm tělesa, redukovanou délku kyvadla, dostaneme bod ${\displaystyle O^{\prime }}$. Tento bod se nazývá střed kyvu a má tu vlastnost, že těleso, zavěšené na ose procházející bodem ${\displaystyle O^{\prime }}$ má stejnou periodu, jako těleso zavěšené v bodě ${\displaystyle O}$.

Je-li totiž moment setrvačnosti tělesa k ose jdoucí těžištěm ${\displaystyle J_{0}}$ a jeho moment setrvačnosti kolem rovnoběžné osy kyvu ${\displaystyle J}$, pak redukovaná délka je

${\displaystyle l={\frac {J_{0}+ma^{2}}{ma}}={\frac {J_{0}}{ma}}+a}$,

kde ${\displaystyle a}$ označuje vzdálenost těžiště od bodu ${\displaystyle O}$.

Kýve-li se těleso kolem středu kyvu ${\displaystyle O^{\prime }}$, platí podle Steinerovy věty

${\displaystyle J^{\prime }=J_{0}+m{(l-a)}^{2}}$

Pro redukovanou délku dostaneme

${\displaystyle l^{\prime }={\frac {J^{\prime }}{m(l-a)}}={\frac {J_{0}}{m(l-a)}}+(l-a)}$

Z předchozích vztahů pak plyne

${\displaystyle l^{\prime }=a{\frac {l-a}{l-a}}+(l-a)=l}$

Redukovaná délka pro osu ${\displaystyle O^{\prime }}$ je tedy stejná jako pro původní osu ${\displaystyle O}$.

Pokud je těleso zavěšeno v bodě ${\displaystyle O^{\prime }}$, který je od bodu ${\displaystyle O}$ vzdálen o redukovanou délku ${\displaystyle l}$, dostaneme tzv. reverzní (převratné) kyvadlo. Perioda převratného kyvadla je opět dána vztahem

${\displaystyle T=2\pi {\sqrt {\frac {l}{g}}}}$.

• Fyzické kyvadlo
• Torzní kyvadlo

• Obrázky, zvuky či videa k tématu matematické kyvadlo na Wikimedia Commons