Metoda sečen

Metoda sečen je iterační numerická metoda užívaná v numerické matematice k hledání kořene funkce jedné reálné proměnné (tj. hledání nějakého řešení rovnice ${\displaystyle f(x)=0}$). K nalezení řešení je obvykle potřeba méně iterací než u metody půlení intervalů. Jako u jiných numerických metod, ani metoda sečen není univerzální a může nastat případ, kdy nekonverguje ke správnému řešení. V těchto případech je nutné použít jinou numerickou metodu.

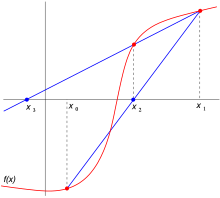
Na začátku je zapotřebí určit dvě počáteční hodnoty ${\displaystyle x_{0}}$ a ${\displaystyle x_{1}}$, které by měly být co nejblíže řešení rovnice ${\displaystyle f(x)=0}$. Tento kořen nemusí ležet mezi hodnotami ${\displaystyle x_{0}}$ a ${\displaystyle x_{1}}$. Pokud však je funkce ${\displaystyle f}$ spojitá a její funkční hodnoty v bodech ${\displaystyle x_{0}}$ a ${\displaystyle x_{1}}$ mají opačná znaménka, nachází se v intervalu ${\displaystyle (x_{0},x_{1})}$ alespoň jeden kořen. Sečna je v tomto případě lineární interpolací funkce ${\displaystyle f}$. Nejsou-li tyto podmínky splněny, výpočet metodou sečen může selhat (a funkce ani nemusí mít reálný kořen).

Pomocí bodů ${\displaystyle x_{0}}$ a ${\displaystyle x_{1}}$ je dána rovnice sečny ke grafu funkce ${\displaystyle f(x)=0}$ v bodech ${\displaystyle P_{0}=[x_{0},f(x_{0})]}$ a ${\displaystyle P_{1}=[x_{1},f(x_{1})]}$ ve tvaru:

${\displaystyle y=f(x_{1})+{\frac {f(x_{1})-f(x_{0})}{x_{1}-x_{0}}}(x-x_{1})}$.

V druhé iteraci musíme určit hodnotu ${\displaystyle x_{2}}$. Hodnota ${\displaystyle x_{2}}$ je průsečíkem sečny dané body ${\displaystyle x_{0}}$ a ${\displaystyle x_{1}}$ a osy x. Stačí do rovnice sečny dosadit ${\displaystyle y=0}$ a vyjádřit ${\displaystyle x}$. Dostaneme rovnici:

${\displaystyle x=x_{1}-{\frac {f(x_{1})(x_{1}-x_{0})}{f(x_{1})-f(x_{0})}}}$,

jejímž řešením je hledaná hodnota ${\displaystyle x_{2}}$. Dále pokračujeme v algoritmu, kde pro ${\displaystyle n>0}$ se hodnota ${\displaystyle x_{n+1}}$ vypočítá z hodnot ${\displaystyle x_{n}}$ a ${\displaystyle x_{n-1}}$ pomocí vztahu:

${\displaystyle x_{n+1}=x_{n}-{\frac {f(x_{n})(x_{n}-x_{n-1})}{f(x_{n})-f(x_{n-1})}}}$.

V algoritmu se pokračuje, dokud není splněna jedna z ukončujících podmínek.

Metoda sečen je přibližná metoda. Výpočet se obvykle ukončuje, pokud absolutní hodnota rozdílu hodnot ${\displaystyle x_{n}}$ a ${\displaystyle x_{n-1}}$ je menší než požadovaná přesnost výsledku ${\displaystyle p>0}$ tedy ${\displaystyle |x_{n}-x_{n-1}|<p.}$

Pokud nejsou splněny podmínky konvergence metody, může se stát, že by výpočet nikdy neskončil. Proto by měl algoritmus obsahovat omezení počtu iterací, jehož dosažení se interpretuje jako selhání metody.

Najděte kořen rovnice ${\displaystyle x^{3}-4x^{2}+6x-24=0}$ v intervalu ${\displaystyle \langle 3,5\rangle }$ a přesností ${\displaystyle p=0{,}01}$.

Za počáteční hodnoty zvolíme ${\displaystyle x_{0}=3}$ a ${\displaystyle x_{1}=5}$. Počítáme dosazováním do vzorce: 

${\displaystyle x_{2}=x_{1}-{\frac {f(x_{1})(x_{1}-x_{0})}{f(x_{1})-f(x_{0})}}=5-{\frac {31(5-3)}{31-(-15)}}=3{,}652174}$.

Další iterace jsou znázorněny v tabulce:

Z tabulky je patrné, že u šesté iterace je ${\displaystyle p<0{,}01}$ a hledaný kořen rovnice ${\displaystyle x^{3}-4x^{2}+6x-24=0}$ v intervalu ${\displaystyle \langle 3,5\rangle }$ a přesností ${\displaystyle p=0{,}01}$ je ${\displaystyle x=4}$.
(V tabulce je kořen 3,999997, ale s zaokrouhlením na setiny dostáváme 4)

Mezi výhody této metody patří malý počet iterací pro nalezení kořene a snadné naprogramování algoritmu v programovacím jazyce. Naopak mezi nevýhody patří, že ne vždy dojde v této metodě ke konvergenci.

• Metoda tečen
• Metoda Monte Carlo
• Půlení intervalů
• Iterace

CHAPRA, Steven C. Numerical Methods for Engineers 6 edition. 1. vyd. [s.l.]: McGraw-Hill, 2009. ISBN 9780073401065. 

VITÁSEK, Emil. Numerické metody. 1. vyd. Praha: SNTL, 1987. 512 s.