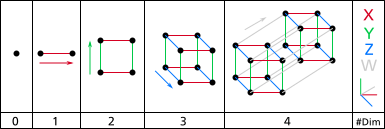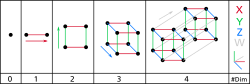Nadkrychle

Nadkrychle neboli hyperkrychle je zobecnění krychle do více rozměrů. Z geometrického hlediska může být d-rozměrná nadkrychle definována jako rovnoběžnostěn d navzájem kolmých vektorů shodné velikosti, tedy např. vektorů [1, 0, 0, …], [0, 1, 0, …], …, […, 0, 0, 1].

Z kombinatorického úhlu pohledu nás zajímají pouze vrcholy a jejich spojení (tj. odpovídající graf): pak můžeme definovat množinu vrcholů jako množinu všech dvojkových zápisů délky d, množinu hran budou tvořit právě takové dvojice vrcholů, které se ve dvojkovém zápise liší právě na jednom místě.

Nadkrychle konkrétní dimenze se označují řeckou číselnou předponou a příponou "rakt", pro čtyři dimenze a víc jde tedy teserakt, penterakt, hexerakt, hepterakt, okterakt... Jinou možností zápisu je n-nadkrychle, kde n značí zamýšlenou dimenzi.

Konstrukce

0 – Bod je nadkrychle nulové dimenze.

1 – Pohybem tohoto bodu v libovolném daném směru do jednotkové vzdálenosti vyznačíme jednotkovou úsečku. To je nadkrychle dimenze jedna.

2 – Úsečkou budeme pohybovat ve směru kolmém na její původní pozici. Tak získáme čtverec, 2-nadkrychli.

3 – Tento čtverec určuje rovinu, vůči které jím budeme opět v kolmém směru pohybovat. Tak dostaneme jednotkovou 3-nadkrychli – prostě krychli.

4 – V třírozměrném prostoru kolmý směr vůči třírozměrné krychli nenajdeme, ale ve čtyřrozměrném dva takové existují a tak v ní můžeme vytvořit 4-nadkrychli, teserakt.

Tak můžeme pokračovat libovolně dál. Tento proces odpovídá matematickému pojmu Minkowského součtu: d-nadkrychle je Minkowského součet d navzájem kolmých jednotkových úseček.

Kombinatorický pohled na pětirozměrnou nadkrychli

Hyperkrychle ve výpočetní technice

Ve výpočetní technice hyperkrychle definuje speciální typ paralelního počítače, jehož procesory, nebo zpracovávající elementy (PEs), jsou propojeny stejně jako vrcholy hyperkrychle. Toto zapojení umožňuje velmi rychlou komunikaci (nejdelší vzdálenost mezi procesory je rovna dimenzi hyperkrychle). Úlohy psané pro hypotetický počítač s n navzájem spojenými procesory (každý s každým) lze tedy v této architektuře počítat maximálně v čase log2(n) krát delším. Většinu reálných úloh lze dokonce počítat stejně rychle jako na počítači s kompletně propojenými procesory.

N-dimenzní hyperkrychlový počítač má 2ⁿ PEs, každý je propojen s n dalšími PEs.

Protože pro každou dimenzi hyperkrychle je třeba jeden komunikační port na každém procesoru, (například u hyperkrychle o dimenzi 16, která má 65 536 vrcholů (procesorů) by každý procesor musel mít 16 portů), bylo by třeba mít procesory s velkou rezervou portů pro konstrukci počítačů s různým počtem procesorů. Zapojení lze ale upravit tak, že v každém vrcholu jsou procesory pouze se třemi porty. Ty jsou uspořádány do kruhu (v jednom vrcholu n-dimenzionální krychle je n procesorů). Dva porty slouží pro komunikaci po kruhu v rámci vrcholu krychle, jeden pak pro komunikaci s jiným vrcholem.

Reference

V tomto článku byl použit překlad textu z článku Hypercube na anglické Wikipedii.

Externí odkazy

• Obrázky, zvuky či videa k tématu nadkrychle na Wikimedia Commons