Nosník na pružném podkladu
Mezi staticky neurčité úlohy mechaniky patří také nosník na pružném podkladu (podloží). Je to obecně křivý nebo přímý nosník, který je spojitě podepřen nebo obklopen podložím buď po celé délce nebo části své délky. Vlivem zatížení se nosník deformuje a vtlačuje do podloží. Dochází tedy k průhybu nosníku a zároveň také ke stlačování podloží. Úlohy řešení nosníků na pružném podkladu se vyskytují při řešení základů různých staveb a konstrukcí, při vyztužování v dolech, tunelech a výkopových pracích, při řešení podzemních potrubních systémů, při navrhování kolejnic v železniční dopravě, v lodním stavitelství, při sportu (např. lyže na sněhu), při výpočtu namáhání mostních plovoucích pontonových konstrukcí pro ženijní vojsko, interakci kostí se šrouby v chirurgii, výpočtu namáhání kořenového systému rostlin atp. Obvykle se nosníky na pružném podkladu dělí na krátké, dlouhé a velmi dlouhé (nekonečné či polonekonečné délky).[1][2][3][4][5]
- Zevní fixátor pro léčbu komplikovaných zlomenin pánve a acetabula (1 - Schanzovy šrouby se zavrtávají do kosti jako do pružného podkladu, 2 - spojky tyčí, 3 - tyče)
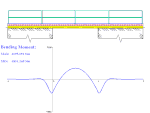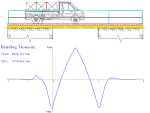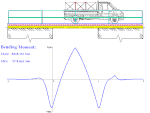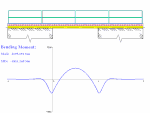
- Automobil přejíždějící most - průběh ohybového momentu v nosníku nekonečné délky, který je částečně uložen na pružném podkladu
- Pružný podklad jako jednodušší model interakce mezi pláštěm Země a zemskou kůrou.
Pružný podklad
Běžné případy z praxe lze značně zjednodušit zavedením vhodného modelu podkladu a pak je možné v některých případech získat analytické řešení. Odezva v podloží se pak nemusí vůbec řešit.
Jestliže je spojitá reakce v podloží qR /Nm−1/ přímo úměrná průhybu v /m/ nosníku nebo přímo úměrná derivacím průhybu a podloží se trvale nedeformuje, pak je nosník uložen na pružném podkladu. V opačném případě je podklad plně nebo částečně poddajný (nepružný).
Modely pružného podkladu
Důvěryhodné modely pružného podkladu je nutné stanovovat na základě experimentu ve spojení s vtlačováním konstrukce do podloží (vyhodnocování zatížení v závislosti na průhybu). Existuje několik modelů pružného podkladu zaměřujících se především na ohybové zatěžování nosníku či desek.
Lineární modely
- Winklerův pružný podklad (jednoparametrický model)
Pružný podklad tzv. Winklerův (poprvé publikovaný v Praze v r. 1867[6]), je nejstarším, nejběžnějším a nejjednodušším modelem podloží. Případné možné plastické deformace podloží se neuvažují. Winklerův model předpokládá, že spojitá reakce podloží qR je přímo úměrná průhybu v v daném místě. Platí tedy qR=k*v), kde k /Nm−2/) je konstanta úměrnosti (koeficient podloží, koeficient ložnosti). Konstantu k lze spolehlivě stanovit jen z měření, případně lze použít vztah k=K*B, kde B /m/ je příčná šířka stykové plochy nosníku s podložím a K /Nm−3/ je modul stlačitelnosti podloží. Modul stlačitelnosti podloží je obecně proměnlivý a náhodný parametr závislý na typu podloží a jeho kvalitě či stupni degradace, ročním období, vlhkosti a teplotě. Nicméně, orientačně platí následující tabulka charakteristických hodnot:[2][5]
| Druh podloží | K /Nm−3/ | |
|---|---|---|
| Suchý nebo vlhký písek | Kyprý (nezhutněný) | 8e6 až 2.5e7 |
| Středně zhutněný | 2.5e7 až 1.25e8 | |
| Těžký (silně zhutněný) | 1.25e8 až 3.75e8 | |
| Mokrý (nasycený) písek | Kyprý (nezhutněný) | 1e7 až 1.5e7 |
| Středně zhutněný | 3.5e7 až 4e7 | |
| Těžký (silně zhutněný) | 1.3e8 až 1.5e8 | |
| Jíl | Tuhý | 1e7 až 2.5e7 |
| Velmi tuhý | 2.5e7 až 5e7 | |
| Tvrdý | více než 5e7 | |
| Půda střední hustoty | 4.9e6 až 4.9e7 | |
| Hustá půda | 4.9e7 až 9.8e7 | |
| Kamenné zdivo | 3.9e9 až 5.9e9 | |
| Beton | 7.8e9 až 1.47e10 | |
- Víceparametrické modely
Víceparametrické modely pružného podkladu vyjadřují spojitou reakci podloží qR jako přímo úměrnou průhybu v a také přímo úměrnou derivacím průhybu (tj. např. dv/dx a vyšší derivace). Nicméně, experimentální stanovení podoby těchto modelů je náročnější. Zde stojí za zmínku uvést například modely autorů Pasternak, Hetényi, Filonenko-Borodich, Kerr, Reissner a Vlasov-Leontiev.[2][7][8][5]
Nelineární modely
Podobně jako lineární modely mohou být jednoparametrické či víceparametrické. Obvykle bývají stanoveny nelineární regresí výsledku experimentů (proložení závislostí zatížení na průhybu vhodnou aproximační funkcí), tj. qR=f(v, dv/dx, zatížení, ...).
Dalším příkladem nelineárního modelu je unilaterální (jednosměrný) Winklerův model, který umožňuje i odlepení od podloží.[9]
Diferenciální rovnice nosníků na pružném podkladu
Vnitřní statické účinky, průhyby a napětí v nosníku na pružném podkladu lze řešit pomocí diferenciálních rovnic.
Odvození (statická úloha)
Odvození je provedeno za následujících předpokladů[1][2][5]
- Nosník vyhovuje podmínce rovinného ohybu.
- Deformace jsou malé a materiál nosníku je homogenní a izotropní a také vyhovuje Hookeovu zákonu.
- Vychází se z rovnováhy sil a momentů působících na element nosníku infinitezimální délky dx /m/, viz následující obrázek.
Vlivem zátěžných účinků se rovný úsek nosníku dx zatlačuje do podloží a také ohýbá. Tato skutečnost se projeví změnou poloměru křivosti r /m/, indukováním vnitřních statických účinků (tj. normálové síly N /N/, posouvající síly T /N/ a ohybového momentu Mo /Nm/) a samozřejmě také spojitou reakcí v podloží qR. Z podmínek rovnováhy sil ve svislém směru a rovnováhy momentů k bodu 2*, pak vyplývají Schwedlerovy věty (nazývané také jako Schwedler-Žuravského věty), které je nutno dosadit do diferenciální rovnice ohybu. Podle [1],[2] a [5] a následujícího obrázku pak lze odvodit diferenciální rovnici ohybu nosníku na pružném podkladu, kde h /m/ je výška nosníku, q /Nm−1/ je spojité zatížení, t2-t1 /K/ je rozdíl teploty mezi dolní a horní částí nosníku, αt /K−1/ je součinitel teplotní délkové roztažnosti, E /Pa/ je modul pružnosti v tahu, G /Pa/ je modul pružnosti ve smyku, β /1/ je součinitel rozložení smykového napětí po průřezu nosníku, JZT /m4/ je hlavní kvadratický moment průřezu nosníku počítaný k ose Z (tj. k ose kolmé na rovinu XY) a S /m2/ je plocha příčného průřezu nosníku. Blíže[2] a [5].
Diferenciální rovnice nosníků na Winklerově pružném podkladu
Nejjednodušším tvarem rovnice ohybu nosníku na pružném podkladu je diferenciální rovnice pro Winklerův pružný podklad.[1][2][5].
Odkazy
Reference
- ↑ a b c d HETÉNYI, Miklos. Beams on Elastic Foundation. [s.l.]: Ann Arbor, University of Michigan Studies, USA, 1946.
- ↑ a b c d e f g h i j k l FRYDRÝŠEK, Karel. Nosníky a rámy na pružném podkladu 1. 1. vyd. Ostrava, Česko: VŠB-TU Ostrava, Fakulta strojní, 2006. 463 s. ISBN 80-248-1244-4.
- ↑ MELERSKI, E., S. Design Analysis of Beams, Circular Plates and Cylindrical Tanks on Elastic Foundations. 2nd. vyd. London, UK: Taylor & Francis Group, 2006. ISBN 978-0-415-38350-9. S. 284.
- ↑ TSUDIK, E. Analysis of Beams and Frames on Elastic Foundation. USA: Trafford Publishing ISBN 1-4120-7950-0. S. 248.
- ↑ a b c d e f g h i j k l FRYDRÝŠEK, Karel; TVRDÁ, Katarína; JANČO, Roland; ET AL. Handbook of Structures on Elastic Foundation. 1st. vyd. Ostrava, Czech Republic: VSB - Technical University of Ostrava, 2013. ISBN 978-80-248-3238-8. S. 1-1691.
- ↑ WINKLER, E. Die Lehre von der Elastiziat und Festigkeit. 1.. vyd. Praha: H. Dominicus, 1867.
- ↑ FRYDRÝŠEK, Karel; JANČO, Roland et al. Nosníky a rámy na pružném podkladu 2. 1. vyd. Ostrava, Česko: VŠB-TU Ostrava, Fakulta strojní, 2008. 516 s. ISBN 978-80-248-1743-9.
- ↑ FRYDRÝŠEK, Karel; NIKODÝM, Marek et al. Beams and Frames on Elastic Foundation 3 (Nosníky a rámy na pružném podkladu 3). 1.. vyd. Ostrava, Česko: VŠB-TU Ostrava, Fakulta strojní, 2013. 611 s. ISBN 978-80-248-2257-0.
- ↑ https://www.engmech.cz/improc/2017/0670.pdf
Literatura
V češtině:
- FRYDRÝŠEK, K.: Nosníky a rámy na pružném podkladu 1, monografie, VŠB-TU Ostrava, Fakulta strojní, Ostrava, Česko, 2006, pp.463, ISBN 80-248-1244-4.
- FRYDRÝŠEK, K., JANČO, R. et al: Nosníky a rámy na pružném podkladu 2, monografie, VŠB-TU Ostrava, Fakulta strojní, Ostrava, Česko, 2008, pp.516, ISBN 978-80-248-1743-9.
- FRYDRÝŠEK, K., NIKODÝM, M. et al: Beams and Frames on Elastic Foundation 3 (Nosníky a rámy na pružném podkladu 3), monografie, VŠB-TU Ostrava, Fakulta strojní, Ostrava, Česko, 2013, pp.611, ISBN 978-80-248-2257-0.
- FRYDRÝŠEK, K., MARVALOVÁ, B., JÁGROVÁ, B.: Vybrané kapitoly z pružnosti a plasticity 1, skriptum, VŠB-TU Ostrava, Fakulta strojní, Ostrava, Česko, 2008, pp.127, ISBN 978-80-248-1855-9.
V angličtině:
- HETÉNYI, M.: Beams on Elastic Foundation, Ann Arbor, University of Michigan Studies, USA, 1946.
- MELERSKI, E., S.: Design Analysis of Beams, Circular Plates and Cylindrical Tanks on Elastic Foundations, 2nd edition, Taylor & Francis Group, London, UK, 2006, pp.284, ISBN 978-0-415-38350-9.
- TSUDIK, E., Analysis of Beams and Frames on Elastic Foundation, Trafford Publishing, USA, pp.248, ISBN 1-4120-7950-0.
- JONES, G., JONES, M.: Analysis of Beams on Elastic Foundations: Using Finite Difference Theory, Thomas Telford Publishing, London, 1997, UK, pp.164, ISBN 978-0727725752.
- FRYDRÝŠEK, K., NIKODÝM, M. et al: Beams and Frames on Elastic Foundation 3 (Nosníky a rámy na pružném podkladu 3), monografie, VŠB-TU Ostrava, Fakulta strojní, Ostrava, Česko, 2013, pp.611, ISBN 978-80-248-2257-0.
V němčině (historická)
- WINKLER, E.: Die Lehre von der Elastiziat und Festigkeit, H. Dominicus, Praha, 1867.
Média použitá na této stránce
Autor: Fry72 Karel Frydrýšek, Licence: CC BY-SA 4.0
Přejezd automobilu po mostě - průběh ohybového momentu v nosníku (řešení pro nekonečný nosník uložený na pružném podkladu)
Autor: Fry72 Karel Frydrýšek, Licence: CC BY-SA 4.0
Element přímého nosníku na pružném podkladu (Rovnováha) Element of a Straight Beam on Elastic Foundation (Equilibrium)
Autor: Fry72 Karel Frydrýšek, Licence: CC BY-SA 4.0
Example of a Beam on Elastic Foundation
Autor: Fry72 Karel Frydrýšek, Licence: CC BY-SA 3.0
Nosník na pružném podkladu
Autor: Fry72 Karel Frydrýšek, Licence: CC BY-SA 3.0
Příklad nosníků na pružném podkladu
Autor: Fry72 Karel Frydrýšek, Licence: CC BY-SA 4.0
Odvození diferenciální rovnice nosníku na obecném pružném podkladu Derivation of the differential equation for the beam on a general elastic foundation
Autor: Fry72 Karel Frydrýšek, Licence: CC BY-SA 4.0
Externí fixátor pro léčbu komplikovaných zlomenin pánve a acetabula
Autor: Fry72, Karel Frydrýšek, Licence: CC BY-SA 4.0
Planeta Země a příklad její možná diskretizace (aplikace pružného podkladu)