Nové definice SI

Mezinárodní výbor pro míry a váhy (CIPM) navrhl v roce 2011 změnu definic základních jednotek soustavy SI,^[1][2] která byla přijatá v roce 2018 a vstoupila v platnost v květnu 2019. Sada sedmi základních jednotek jako takových zůstala zachována: metr, kilogram, sekunda, kelvin, ampér, kandela a mol. Staré definice sekundy, metru a kandely byly považovány za vyhovující, a proto se změnily jen jejich formulace s ohledem na jednotný formát pro všechny jednotky. Definice kilogramu, ampéru, kelvinu a molu byly ale principiálně změněny tak, že každá z těchto jednotek je pevně spjata s určitou neměnnou vlastností přírody. Důležitým požadavkem na nové definice byla samozřejmě zpětná kompatibilita, tedy aby nové jednotky byly stejně velké jako stávající s maximální dosažitelnou přesností.

Protože byly splněny všechny klíčové podmínky požadované pro zavedení (přesnost nových metod realizace etalonů^[3] i nová adjustace fundamentálních fyzikálních konstant^[4]), Generální konference pro míry a váhy (CGPM) schválila změnu definic na svém 26. zasedání ve Versailles 16. listopadu 2018.^[5][6][7] Změna vstoupila v platnost 20. května 2019, tedy symbolicky ve Světový den metrologie, který je výročím přijetí Metrické konvence.^[5][8]

Řada autorů^{[zdroj⁠?!][9]} vyjadřuje kritiku vůči některým definicím - včetně toho, že návrh nedokázal řešit dopad rozbití vazby mezi definicí daltonu a definicemi kilogramu, molu a Avogadrovy konstanty.

Kilogram je jako poslední z jednotek SI definován fyzickým etalonem, mezinárodním prototypem kilogramu, se kterým je třeba porovnávat hmotnosti všech ostatních těles. Nelze ovšem zaručit, že hmotnost prototypu je absolutně stálá. Porovnávání s kanonickými kopiemi spíše naznačuje, že relativní nejistota měření je v řádu 10⁻⁸, tedy že hmotnost prototypu se přes veškerou snahu časem mění řádově o desítky mikrogramů. Přitom na definici kilogramu v současnosti závisí i jednotky ampér, mol a kandela, takže i jejich hodnoty mohou být považovány za časově ne zcela stabilní. Z těchto důvodů vznikla iniciativa definovat všechny jednotky pouze slovně, na základě neměnných vlastností přírody, k jejichž realizaci není potřeba konkrétní etalon.^{[10][11][12][1]}

Současná definice kelvinu, jednotky termodynamické teploty, je vázána na pevnou vlastnost přírody: teplotu trojného bodu vody. To se zdá být principiálně správné, ale praktická realizace naráží na problémy. Přesná teplota trojného bodu až příliš závisí na chemické čistotě a izotopovém složení použité vody. Navíc je technicky obtížné tuto definici používat při velmi nízkých teplotách, blízkých absolutní nule. Proto i kelvin má být definován novým způsobem.^[12][1]

Současná definice ampéru (a všech jednotek od něj odvozených) na základě magnetické síly působící mezi nekonečně dlouhými vodiči s elektrickým proudem rovněž naráží na problémy při praktické realizaci. Z toho důvodu už mnoho národních standardizačních úřadů používá etalony elektrických veličin založené na kvantovém Hallově jevu resp. Josephsonově jevu, jejichž elektrický odpor resp. elektrické napětí má fyzikálně jednoznačný vztah k hodnotě Planckovy konstanty a elementárního náboje. Navržené definice se přizpůsobily této praxi.^{[10][12][11][1]}

V minulosti se velmi osvědčily stávající definice jednotek sekunda a metr. Pouze tyto dvě jednotky zůstanou v novém systému absolutně stejně velké jako dříve. Sekunda je definována na základě vlastností atomu cesia, které jsou považovány za zcela stabilní, a v praxi je úspěšně realizována atomovými hodinami (tzv. cesiový standard). Metr je definován s využitím předchozí definice sekundy na základě pevné hodnoty rychlosti světla ve vakuu, která patří mezi základní fyzikální konstanty. Praktičnost těchto definic motivuje snahu formulovat definice ostatních jednotek stejným způsobem: stanovením přesné číselné hodnoty určité fyzikální konstanty.^[6]

Pro snazší pochopení nového systému a zdůraznění této základní myšlenky jsou definice všech 7 základních jednotek přeformulovány tak, aby byla explicitně uvedena konstanta, jejíž číselná hodnota je definicí fixována. Jde o principiálně stejný způsob, jakým se ve fyzice běžně definují přirozené jednotky.^[2]

Definice sedmi základních jednotek vyžaduje stanovit číselné hodnoty vybraných sedmi fyzikálních veličin, které jsou obecně považovány za konstantní. CIPM ve svém návrhu, aktualizovaném začátkem roku 2018, zvolil tyto konstanty^[6][13] (návrh již respektuje novou speciální adjustaci konstant CODATA 2017^[4]):

• frekvence záření, které vzniká při přechodu atomu cesia 133 mezi dvěma energetickými hladinami velmi jemné struktury základního stavu: Δν_Cs = 9 192 631 770 Hz;
• rychlost světla ve vakuu: c = 299 792 458 m/s;
• Planckova konstanta: h = 6,626 070 15×10⁻³⁴ J s;
• elementární náboj: e = 1,602 176 634×10⁻¹⁹ C;
• Boltzmannova konstanta: k = 1,380 649×10⁻²³ J/K;
• Avogadrova konstanta: N_A = 6,022 140 76×10²³ mol⁻¹;
• světelná účinnost monochromatického záření o frekvenci 540 THz: K_cd = 683 lm/W.

Nové definice jednotek^[13] jsou uvedeny v takovém pořadí, aby každá závisela pouze na definicích již uvedených. Z toho je zřejmé, že nenastává definice kruhem. Pro srovnání jsou uvedeny i definice platné do května 2019.

Stará definice

Sekunda je doba trvání 9 192 631 770 period záření odpovídajícího přechodu mezi dvěma hladinami velmi jemné struktury základního stavu atomu cesia 133.

Později bylo upřesněno, že atom cesia musí být v klidu a teplota pozadí blízká 0 K. Ze třetího zákona termodynamiky plyne, že teplota absolutní nuly je nedosažitelná. Lze se k ní však libovolně přiblížit. Podmínku nulové termodynamické teploty je třeba chápat tak, že cesiové hodiny musí provádět korekce s ohledem na teplotu pozadí.

Návrh nové definice

Sekunda, značka „s“, je jednotka času v SI. Je definována fixací číselné hodnoty cesiové frekvence Δν_Cs, tedy frekvence přechodu mezi hladinami velmi jemného rozštěpení neporušeného základního stavu atomu cesia 133, aby byla rovna 9 192 631 770, je-li vyjádřena jednotkou Hz, rovnou s⁻¹.

Nová formulace je obsahově zcela shodná se stávající, včetně podmínek pro emisi záření. Neporušeným stavem se rozumí stav izolovaného atomu cesia nenarušený žádným vnějším polem, tedy ani zářením černého tělesa odpovídajícím teplotě okolního prostředí. Časem se rozumí vlastní čas z pohledu obecné teorie relativity. Nově definované podmínky jsou tak totožné s podmínkami předchozí definice (v klidu při teplotě 0 K). Liší se jen formálně, aby definice měla stejný formát jako ostatní navrhované definice, čímž vynikne idea, že každá jednotka je svázána s určitou neměnnou vlastností přírody.

Až na formální znění tedy zůstala definice sekundy nezměněna. Vzhledem k pokroku v metrologii času a frekvence se však uvažuje o budoucí faktické redefinici i u sekundy, která by měla vstoupit v platnost ještě před rokem 2030, podle předběžných předpokladů nejspíše v roce 2026.^[14][15] Precizní definice a realizace sekundy je velmi důležitá, protože v novém systému jsou definice všech jednotek kromě molu od sekundy odvozené.

Stará definice

Metr je vzdálenost, kterou urazí světlo ve vakuu za dobu 1/299 792 458 sekundy.

Nová definice

Metr, značka „m“, je jednotka délky v SI. Je definována fixací číselné hodnoty rychlosti světla ve vakuu c, aby byla rovna 299 792 458, je-li vyjádřena jednotkou m s⁻¹, kde sekunda je definována pomocí cesiové frekvence Δν_Cs.

Také zde jsou obě formulace ekvivalentní. Definicí metru je přesně stanovena vlnová délka mikrovlnného záření, které je uvedeno v definici sekundy, vztahem

${\displaystyle \lambda ={\frac {c}{f}}={\frac {299792458}{9192631770}}\,\mathrm {m} \approx 3{,}2612\dots \,\mathrm {cm} \,.}$

Porovnání neznámé vzdálenosti s touto vlnovou délkou lze provádět interferometricky.

Stará definice

Kilogram je jednotka hmotnosti; je rovna hmotnosti mezinárodního prototypu kilogramu.

Nová definice

Kilogram, značka „kg“, je jednotka hmotnosti v SI. Je definována fixací číselné hodnoty Planckovy konstanty h, aby byla rovna 6,626 070 15×10⁻³⁴, je-li vyjádřena jednotkou J s, rovnou kg m² s⁻¹, kde metr a sekunda jsou definovány pomocí c a Δν_Cs.

Toto byla nejpodstatnější z přijatých změn. Definice založená na prototypu byla v platnosti již od první konference CGPM v roce 1889 a bylo zřejmé, že má své meze. Spojení se základní fyzikální konstantou nově umožnilo, aby velikost kilogramu a všech jednotek od něj odvozených byla spolehlivě časově stabilní. Planckova konstanta h je základní konstantou kvantové teorie, kde určuje mimo jiné vztah mezi energií a frekvencí fotonu: E=hf. Speciální teorie relativity poskytuje vztah mezi energií a hmotností, kde konstantou úměrnosti je rychlost světla ve vakuu: E=mc². Tyto dva fyzikální zákony umožňují odvodit definici kilogramu od číselné hodnoty Planckovy konstanty. K měření hmotnosti podle nových definic lze v praxi použít wattové váhy, přičemž se využije i nová definice ampéru.

Stará definice

Ampér je stálý elektrický proud, který protéká dvěma rovnoběžnými nekonečně dlouhými vodiči o zanedbatelném průřezu umístěnými ve vakuu 1 m od sebe, jestliže mezi vodiči působí magnetická síla o velikosti 2×10⁻⁷ newtonu na jeden metr délky vodiče.

Vyjádřeno jinými slovy: „Permeabilita vakua ${\displaystyle \mu _{0}}$ má hodnotu přesně ${\displaystyle 4\pi \times 10^{-7}}$ H/m.“

Nová definice

Ampér, značka „A“, je jednotka elektrického proudu v SI. Je definována fixací číselné hodnoty elementárního náboje, aby byla rovna 1,602 176 634×10⁻¹⁹, je-li vyjádřena jednotkou C, rovnou A s, kde sekunda je definována pomocí Δν_Cs.

Zafixování elementárního náboje a Planckovy konstanty stanovuje přesně také hodnotu Josephsonovy konstanty ${\displaystyle K_{\mathrm {J} }=2e/h\approx 484\,\mathrm {THz/V} }$ a von Klitzingovy konstanty ${\displaystyle R_{\mathrm {K} }=h/e^{2}\approx 25{,}8\,{\mathrm {k} \Omega }}$, které se vyskytují ve vztazích pro Josephsonův jev resp. kvantový Hallův jev. Tímto způsobem lze vytvořit etalony elektrického napětí U a elektrického odporu R. Realizace ampéru je pak založena na aplikaci Ohmova zákona ${\displaystyle I=U/R}$. Druhou možností je využití jednoelektronové pumpy s přesným taktováním, čímž by byl uzavřen tzv. metrologický trojúhelník.^{[pozn. 1]}

Stará definice

Kelvin, jednotka termodynamické teploty, je rovna zlomku 1/273,16 termodynamické teploty trojného bodu vody.

Nová definice

Kelvin, značka „K“, je jednotka termodynamické teploty v SI. Je definována fixací číselné hodnoty Boltzmannovy konstanty, aby byla rovna 1,380 649×10⁻²³, je-li vyjádřena jednotkou J K⁻¹, rovnou kg  m²s⁻² K⁻¹, kde kilogram, metr a sekunda jsou definovány pomocí h, c a Δν_Cs.

Boltzmannova konstanta ${\displaystyle k}$ je základní konstantou statistické fyziky, kde spojuje entropii s rozdělením pravděpodobnosti mikrostavů systému. Jako konstanta úměrnosti se objevuje ve stavové rovnici ideálního plynu. Určuje také vztah mezi teplotou plynu a pohybovou energií jeho molekul (ekvipartiční teorém). Nová definice kelvinu umožňuje převést měření teploty na měření energie částic, což je v mnoha případech jednodušší, zejména při teplotách extrémně vysokých nebo nízkých.

Stará definice

Mol je látkové množství systému, který obsahuje stejný počet elementárních entit, kolik je atomů v 0,012 kg uhlíku ¹²C.

Tato definice svazuje látkové množství s hmotností. Lze ji vyjádřit slovy: „Relativní atomová hmotnost uhlíku 12 je přesně 12.“

Nová definice

Mol, značka „mol“, je jednotka látkového množství v SI. Je definována fixací číselné hodnoty Avogadrovy konstanty, aby byla rovna 6,022 140 76×10²³, je-li vyjádřena jednotkou mol⁻¹.

Z nové definice je více zřejmé, že látkové množství ${\displaystyle n}$ je veličina zcela nezávislá na ostatních šesti základních veličinách a jednoduše odpovídá počtu ${\displaystyle N}$ částic vybraného typu ve vzorku látky ${\displaystyle n={\frac {N}{N_{\mathrm {A} }}}}$.

Stará definice

Kandela je svítivost zdroje, který vydává monochromatické záření o frekvenci 540×10¹² Hz, jehož intenzita v daném směru je 1/683 wattů na steradián.

Nová definice

Kandela, značka „cd“, je jednotka svítivosti v SI. Je definována fixací číselné hodnoty světelné účinnosti monochromatického záření o frekvenci 540×10¹² Hz, K_cd, aby byla rovna 683, je-li vyjádřena jednotkou lm W⁻¹, rovnou cd sr W⁻¹, nebo cd sr kg⁻¹ m⁻² s³, kde kilogram, metr a sekunda jsou definovány pomocí h, c a Δν_Cs.

Rozdíl mezi těmito definicemi je pouze ve formulacích. Přesto v novém systému není jednotka kandela absolutně stejně velká, protože závisí na definici kilogramu.

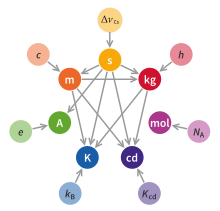
Jednotka mol, která ve stávajícím systému závisí na definici kilogramu, je v novém systému zcela nezávislá na ostatních jednotkách. Tím je zvýrazněna odlišnost veličin hmotnost a látkové množství. Všechny ostatní jednotky naopak odkazují na definici sekundy, která je i nadále určena osvědčeným cesiovým standardem, nezávisle na ostatních základních jednotkách. Definice metru nadále vychází z definice sekundy a de facto určuje vlnovou délku zmíněného záření cesiového atomu podle vztahu ${\displaystyle \lambda =c/f}$. Nová definice kilogramu je vedle Planckovy konstanty založena na definicích metru a sekundy.

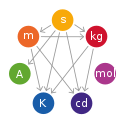
Ostatní závislosti jsou graficky vyznačeny v obrázku. Každé ze sedmi základních jednotek odpovídá hodnota jedné fyzikální konstanty. Srovnání s grafem v úvodu tohoto textu ukazuje, že ampér ani mol v novém systému nepoužívají definici kilogramu, ale nově na ní závisí kelvin.

Normativní určení hodnot vybraných fundamentálních konstant má vliv na další důležité fyzikální konstanty. Některé konstanty a převodní faktory původně zatížené nejistotami měření jsou v novém systému jednotek známy zcela přesně.^[11] Mezi ně patří:

• molární plynová konstanta ${\displaystyle R=N_{\mathrm {A} }k\approx 8{,}31\,\mathrm {J\,K^{-1}\,mol^{-1}} }$,
• Faradayova konstanta ${\displaystyle F=N_{\mathrm {A} }e\approx 9{,}65\times 10^{4}\,\mathrm {C/mol} }$,
• Stefanova–Boltzmannova konstanta ${\displaystyle \sigma ={\frac {2\pi ^{5}k^{4}}{15h^{3}c^{2}}}\approx 5{,}67\times 10^{-8}\,\mathrm {W\,m^{-2}\,K^{-4}} }$,
• Wienova konstanta ${\displaystyle b={\frac {hc}{k\mathrm {x} }}\approx 2{,}90\,\mathrm {mm\,K} }$ (číselný faktor ${\displaystyle \mathrm {x} \approx 4{,}97}$ je přesně určený^{[pozn. 2]}),
• Josephsonova konstanta ${\displaystyle K_{\mathrm {J} }=2e/h\approx 484\,\mathrm {THz/V} }$,
• von Klitzingova konstanta ${\displaystyle R_{\mathrm {K} }=h/e^{2}\approx 25{,}8\,{\mathrm {k} \Omega }}$,
• přepočet mezi SI jednotkou energie joule a často používaným elektronvoltem, který je dán číselnou hodnotou elementárního náboje ${\displaystyle 1\,\mathrm {eV} \approx 1{,}60\times 10^{-19}\,\mathrm {J} }$.

U jiných konstant je situace opačná, původně byly stanoveny přesně a nově jsou zatíženy nejistotou. Zejména jde o vlastnosti fyzikálního vakua:

• permeabilita vakua; ve starém systému přesně μ₀ = 4π×10⁻⁷ H/m (z definice ampéru), v novém systému je dána vztahem ${\displaystyle \mu _{0}={\frac {2h\alpha }{e^{2}c}}={\frac {2\alpha }{c}}R_{\mathrm {K} }={\frac {Z_{0}}{c}}}$, kde α je konstanta jemné struktury,
• permitivita vakua ${\displaystyle \varepsilon _{0}={\frac {1}{\mu _{0}c^{2}}}={\frac {e^{2}}{2hc\alpha }}={\frac {1}{2\alpha cR_{\mathrm {K} }}}={\frac {1}{Z_{0}c}}\approx 8{,}85\times 10^{-12}\,\mathrm {F/m} }$,
• impedance vakua ${\displaystyle Z_{0}=\mu _{0}c={\sqrt {\frac {\mu _{0}}{\varepsilon _{0}}}}={\frac {2h\alpha }{e^{2}}}=2\alpha R_{\mathrm {K} }\approx 377\,\mathrm {\Omega } }$.

Konstanta ${\displaystyle \alpha \approx 1/137}$ je bezrozměrná veličina, takže její hodnotu nelze ovlivnit volbou systému jednotek, je nutné ji změřit. Tabulky CODATA 2018 uvádějí, že je známa s relativní nejistotou 1,5×10⁻¹⁰.^[19] Stejnou nejistotou jsou v novém systému zatíženy i konstanty μ₀, ε₀, Z₀.

Newtonova gravitační konstanta, ačkoli patří mezi fundamentální fyzikální konstanty, není užita v žádné z definic. Dosud totiž nikdo neobjevil způsob, jak určit její jednoznačnou hodnotu s dostatečnou přesností srovnatelnou s přesností jiných konstant. Dle tabulek CODATA 2018 je relativní nejistota 2,2×10⁻⁵, tedy o několik řádů vyšší než u jiných fundamentálních konstant.

Dalton, jiným názvem atomová hmotnostní jednotka, (značka Da nebo u) je jednotka hmotnosti často užívaná v chemii i v atomové a jaderné fyzice. Velikost jednotky přibližně odpovídá hmotnosti nukleonů, ${\displaystyle 1\,\mathrm {Da} \approx 1{,}66\times 10^{-27}\,\mathrm {kg} }$. Je to jediná jednotka závislá na experimentálně určované hodnotě, kterou Mezinárodní úřad pro míry a váhy (BIPM) povoluje užívat zároveň s SI. (Dříve měl tento status také elektronvolt a astronomická jednotka, ale ty jsou již definovány přesně.) Dalton je definován jako 1/12 klidové hmotnosti atomu uhlíku ¹²C v základním stavu. Ve starém systému SI to znamenalo, že platí přesný vztah mezi daltonem a Avogadrovou konstantou:

${\displaystyle 1\,\mathrm {Da} =1\,\mathrm {g\,mol^{-1}} /N_{\mathrm {A} }\,}$, který lze zapsat s využitím tzv. molární hmotnostní konstanty, definované jako M_u = 1 g / mol, a atomové hmotnostní konstanty m_u = 1 Da veličinovou rovnicí

${\displaystyle M_{\mathrm {u} }=N_{\mathrm {A} }m_{\mathrm {u} }\,.}$

Nová definice molu fixuje Avogadrovu konstantu nezávisle na atomech uhlíku, čímž do výše uvedeného vztahu principiálně zasahuje.

Při redefinici se z důvodů kontinuity hodnot relativních atomových hmotností zachovala stávající definice atomové hmotnostní konstanty a tedy i daltonu pomocí experimentálně určené hmotnosti atomu uhlíku 12. Přestala však platit přesná hodnota molární hmotnostní konstanty; ta má nyní stejnou relativní nejistotu jako atomová hmotnostní konstanta resp. dalton (čili atomová hmotnostní jednotka),^{[20][pozn. 3]} třebaže některé metrologické studie se dříve klonily k fixaci hodnoty M_u spojené však s nepatrnými změnami relativních atomových hmotností.^[21]

V roce 1999 konstatovala 21. konference CGPM, že snaha o předefinování kilogramu je opodstatněná a národní laboratoře mají pokračovat v úsilí, které povede k jeho spojení s některou přírodní konstantou. V roce 2007 stanovila 23. konference CGPM podmínky, které musí být splněny před přijetím nových definic kilogramu, ampéru, kelvinu a molu. Na podzim roku 2011 konstatovala 24. konference CGPM, že podmínky sice ještě nejsou zcela splněny, ale došlo k významnému pokroku.^[1] Aby všechny zúčastněné strany získaly podrobnější představu o chystaných změnách, byl zároveň vydán návrh nového znění brožury BIPM, která obsahuje definice jednotek a doporučuje způsoby zacházení s nimi.^[2] Jak ukazuje aktualizované znění,^[13] nové definice se od návrhu podstatně neliší, kromě upřesnění několika posledních platných číslic v hodnotách konstant a případných drobných formulačních změn, vycházejících z připomínek odborné obce k formulační korektnosti.^[22][23]

Rezoluce CGPM jsou připravovány Mezinárodním výborem pro míry a váhy (CIMP), jemuž poskytují odborné poradenství jeho Poradní výbory.

Kilogram, mol

Poradní výbor pro hmotnost a související veličiny (CCM – Consultative Committee for Mass and Related Quantities) při projednávání redefinice kilogramu pomocí univerzálních konstant doporučil, aby byly před redefinicí splněny mimo jiné následující podmínky:

• Pro redefinici kilogramu musejí být provedeny alespoň tři nezávislé experimenty potvrzující hodnoty Planckovy konstanty s relativní rozšířenou nejistotou (95 %) ne větší než 5×10⁻⁸. Alespoň jedna z těchto hodnot by měla mít relativní standardní nejistotu menší (lepší) než 2×10⁻⁸. Do experimentů by měly být zahrnuty projekty Kibble balance a projekt Avogadro.
• Pro každou z odpovídajících konstant by hodnoty vycházející z odlišných experimentů měly být konzistentní na hladině významnosti 95 %.^[24]

V doporučení G1 (2013) ze svého 14. zasedání CCM přeformuloval první podmínku tak, že musí zahrnovat jak experimenty založené na wattových váhách, tak na XRCD (X-ray Crystal Density, tedy určení početní hustoty částic v krystalové mřížce pomocí rentgenového záření). Byly doplněny podmínky co nejpřímějšího porovnání s mezinárodním prototypem kilogramu a validace procedury budoucí realizace kilogramu v souladu se zásadami BIPM MRA.^[25]

První podmínku dosud splnily výsledky wattových vah NIST (2007), projektu Avogadro (2011)^[26] a wattové váhy kanadského NRC. Ty dosáhly v roce 2014 nejistoty 2×10⁻⁸ a jako první tak splnily druhou podmínku.^[27]

Porovnání posledních výsledků jednotlivých experimentů, kterým bylo věnováno samostatné číslo 2 svazku 51 časopisu Metrologia (2014), ukázalo velmi dobrou vzájemnou konzistenci výsledků. Pokrok tak již v roce 2014 naznačil, že redefinice (z pohledu podmínek pro nový kilogram a mol) mohla proběhnout v roce 2018,^[27] Generální konference pro míry a váhy schválila změnu definice na svém 26. zasedání ve Versailles 16. listopadu 2018.

Ampér

U redefinice ampéru byla situace ještě příznivější. Pro 3 ohmicky vzájemně závislé veličiny – elektrický proud, napětí a odpor – existují principiálně vhodné realizace etalonů kvantovaných hodnot závislých pouze na univerzálních konstantách – pro proud jednoelektronová pumpa (proud závisí pouze na elementárním náboji e a taktovací frekvenci), pro napětí Josephsonův přechod (napětí závisí pouze na taktovací frekvenci a Josephsonově konstantě, tedy jen na univerzálních konstantách h, e) a pro odpor zařízení pro kvantový Hallův jev (odpor je realizován jako násobek von Klitzingovy konstanty, závislé též jen na univerzálních konstantách h, e). Praktické realizace však mohou být zatížené sice malými, ale pro velmi přesnou metrologii nezanedbatelnými nejistotami (ať už reálně zjištěnými, jako elektronický šum u zařízení pro kvantový Hallův jev, nebo způsobenými hypotetickými dalšími vlivy). Proto je snaha nejen o zvyšování přesnosti takových etalonů, ale i o hledání nezávislých způsobů realizace, umožňujících s obdobnou přesností vyloučit vliv skrytých systematických chyb.

V roce 2012 se podařilo vytvořit polovodičový obvod, který může sloužit jako standardizovaný etalon kvantovaných hodnot elektrického napětí, realizovaný na principu odlišném od Josephsonova jevu. Vzájemné provázání prvků pro kvantový etalon proudu a odporu (sériové zapojení jednoelektronové pumpy a zařízení pro kvantový Hallův jev) v jednom polovodičovém obvodu představuje fyzikálně nezávislou realizaci napětí a umožňuje vyloučit případné systematické nejistoty josephsonovsky realizovaných napětí vyplývající z hypotetických (i když prokazatelně velmi malých) korekcí dalších vlivů daných fyzikou polovodičů.^[28][29]

V roce 2013 se britským vědcům podařilo vytvořit jednoelektronovou pumpu na bázi grafenu, u které může být dosaženo taktovací frekvence řádu gigahertzů, požadované pro proudový etalon. Stala se tak (vedle nepřímého stanovení přes kvantované napětí a odpor) nejvýznamnějším současným kandidátem na přímou realizaci nově definovaného ampéru.^[17][18]

Vědcům německé Physikalisch-Technische Bundesanstalt se v roce 2013 podařilo vyvinout kvantový proudový standard, který sériovým zapojením jednoelektronových pump omezuje nepřesnosti stochastického charakteru způsobené tunelovým jevem. Navíc nejen generuje taktovaný jednoelektronový proud, ale současně a nezávisle tento proud měří.^[30][31] V roce 2016 se jim podařilo zvýšit přesnost tohoto měření a dosáhnout relativní chyby pouhých 1,6×10⁻⁷.^[32]

Kelvin

Pro novou definici kelvinu doporučil Poradní výbor BIPM pro termometrii (CCT) na svém 25. zasedání v roce 2010, aby před uskutečněním redefinice byla hodnota Boltzmannovy konstanty stanovena s relativní nejistotou v řádu 10⁻⁶ z měření založených na fundamentálně rozdílných metodách primární termometrie, v ideálním případě pomocí akustické plynové termometrie a pomocí termometrie založené na permitivitě plynů, podpořených dalšími metodami, jako termometrií pomocí Johnsonova šumu, radiační termometrií a termometrií pomocí dopplerovského rozšíření, a na základě těchto hodnot by měla být přijata adjustovaná hodnota CODATA.^[33] V roce 2013 se podařilo dosáhnout požadované přesnosti akustickou plynovou termometrií. Hodnota k = 1,380 651 56 (98)×10⁻²³ J·K⁻¹, což představuje nejistotu 0,7×10⁻⁶.^[34][35] S využitím termometrie pomocí permitivity plynů byla v roce 2017 určena hodnota Boltzmannovy konstanty k = 1,380 6482 ×10⁻²³ J·K⁻¹ s relativní nejistotou 1,9×10⁻⁶.^[36]

Reálná redefinice

Okamžik, kdy redefinice vstoupí v platnost, tedy závisel zejména na pokroku v přesnosti a konzistenci určení Planckovy a Boltzmannovy konstanty. V roce 2016 prohlásil Donald Burgess z NIST, že stávající výsledky měření fundamentálních konstant, na kterých budou nové definice SI založeny, již dosáhly přesnosti vyhovující požadavkům na zavedení redefinice.^[3]

Pro závěrečnou etapu před přijetím byl stanoven harmonogram, svazující schválení nových definic s novou adjustací fundamentálních fyzikálních konstant.^[37] Ta byla vydána v roce 2017^[4].

Redefinice byla přijata CGPM na 26. zasedání 16. listopadu 2018^[7] ve Versailles v Paříži.^{[38][39][40][27]} Vstoupení v mezinárodní platnost bylo stanoveno na 20. května 2019, tj. Světový den metrologie, který je výročím přijetí Metrické konvence.^[8] Český Zákon o metrologii, obsahující definice SI,^[41] nebo příloha evropské direktivy 80/181/EEC ^[42] budou muset být také novelizovány a s termínem platnosti redefinice budou muset být vydány i nové revize řady dotčených odborných norem pro veličiny a jednotky, např. řada (ČSN) ISO/IEC 80000 či (ČSN) IEC 60050. Následovat by mělo vydání nové adjustace fundamentálních fyzikálních konstant již v duchu nových definic.^[37]

Vzhledem k pokroku v metrologii času a frekvence se uvažuje o budoucí faktické redefinici i u sekundy.

Stávající i nová definice vycházejí z měření času atomovými cesiovými hodinami, pracujícími na mikrovlnných frekvencích.^[43] Jako slibnější se však jeví nové typy optických atomových hodin, tedy hodin založených na kvantových přechodech s energiemi odpovídajícími frekvencím spektrálního pásma viditelného či ultrafialového záření, u kterých proběhne za 1 sekundu o zhruba 4 až 6 řádů více oscilací a potenciálně tak umožňují řádově vyšší přesnosti než nejpřesnější hodiny cesiové. Mohou to být optické atomové hodiny založené na oktupólovém přechodu v iontu ytterbia ¹⁷¹Yb^+[44], na kvadrupólovém přechodu v iontu stroncia ⁸⁸Sr^+[45][46], ytterbia ¹⁷¹Yb⁺, vápníku ⁴⁰Ca⁺, rtuti ¹⁹⁹Hg⁺ či hodiny s iontem hliníku ²⁷Al⁺ s kvantovou logikou.^[14][47] Kvantová logika, využívající spřažení daného iontu hliníku ²⁷Al⁺ v kvadrupólové elektrické pasti s jiným iontem (např. ²⁵Mg⁺) v dodatečném vnějším magnetickém poli, umožňuje detekovat kvantový stav iontu i aplikovat laserové chlazení, které by jinak nebylo prakticky proveditelné, protože vhodný přechod by odpovídal ultrafialovému záření, a podstatně tak snížit různé příspěvky k relativní neurčitosti frekvence – v roce 2019 se ji podařilo snížit na rekordních 0,94×10⁻¹⁸.^[48]

Jinou slibnou metodou je využití přechodů v neutrálních atomech v optické mřížce, tedy zachycených v potenciálu stojaté elektromagnetické vlny ze dvou protichůdných laserových paprsků. Limitující fundamentální (neodstranitelná) kvantová nejistota tak může být zredukována zprůměrováním a zvýšena tak stabilita a přesnost.^[49][50] Mohou to být hodiny využívající přechodu v atomech stroncia ⁸⁷Sr, ytterbia ¹⁷¹Yb či rtuti ¹⁹⁹Hg.^{[51][52][53][54][55][50][56][57][14]} Rekordní relativní přesnost hodin tohoto typu, dosažená v roce 2018, je 2,5×10⁻¹⁹,^[58][59] ve stejném roce bylo dosaženo i rekordní stability (3,2×10⁻¹⁹) a opakovatelnosti měření.^[60][61][62]

Dalším typem jsou hodiny s kryogenickým paprskem atomů vodíku s dvoufotonovým přechodem 1S-2S.^[14]

Od roku 2011 je znám princip tzv. jaderných hodin, založených na magnetickém dipólovém přechodu mezi energetickými stavy jádra iontu thoria, který by umožňoval dosažení odchylky pouhé 1 s za 200 miliard let (1,6×10⁻¹⁹).^[63][64][65] Oproti atomovým hodinám by jaderné hodiny byly stabilnější a méně podléhající vlivům elektromagnetického šumu. Místo toho, aby byla izolována v elektromagnetické pasti, mohla by být jádra hodin ukotvena v pevném materiálu, což by značně zjednodušilo návrh hodin.^[66]

Případná změna standardních hodin z cesiových na jiný, přesnější typ by znamenala úpravu definice sekundy ve specifikaci přechodu a číselné hodnotě, případně i ve vymezení podmínek. Neměla by žádný vliv na definice ostatních základních jednotek, mohla by však implicitně zvýšit přesnost jejich určování (zejména u metru).

Poradní výbor CIPM pro čas a frekvenci (CCTF) ve svém „Strategickém dokumentu“ navrhuje 5 milníků, které musí být pro redefinici dosaženy. Předpokládají se optické atomové hodiny (slibných je přinejmenším 8 různých typů, založených na jiném energetickém přechodu daného iontu nebo jiném principu). Základem je dosažení takové přesnosti, že nejméně 3 různé (v různých laboratořích nebo různé konstrukce) hodiny nového typu musí mít validovanou nejistotu o zhruba 2 řády lepší než nejlepší cesiové hodiny v té době. Výsledky nezávislých měření daným typem musí být přenositelné, tedy srovnatelné v různých institucích pomocí přenosných hodin či pomocí pokročilých spojení, a to s relativními odchylkami pod 5×10⁻¹⁸, zpřesnění dané redefinicí nezmění výsledek měření nejlepšími cesiovými hodinami v té době (v rámci jejich nejistoty), sekundární reprezentace takové nově definované sekundy umožní regulárně přispívat k TAI a výsledky měření aspoň 5 jinými typy optických atomových hodin budou srovnatelné (s relativními odchylkami pod 5×10⁻¹⁸).^[14][15]

Dosažení stanovených milníků (budou-li takto akceptovány) se předpokládá v roce 2022. S uvážením trvání schvalovacího procesu v poradních výborech a CIPM a vzhledem ke čtyřletému cyklu CGPM by mohla redefinice sekundy proběhnout nejdříve v roce 2026;^[14] odhad vycházející ze současného stavu předpokládá nabytí platnosti ještě před rokem 2030.^[15] Datum 2026 považují za reálné i metrologové předních světových pracovišť pro měření času a frekvence (např. v NIST^[67][68]), a to s přihlédnutím k tomu, že některá kritéria již byla naplněna v roce 2018;^[68] někteří však pochybují, zda se najde dostatečně silný důvod pro reálné upotřebení redefinice a spekulují s oddálením až do raných třicátých let.^[68] Tímto důvodem by však mohla být gravitační astronomie, tedy přesnější a snazší detekce nedávno prokázaných gravitačních vln,^[61] nebo přesnější, centimetrová geodézie.^[60][62][69]

• Obrázky, zvuky či videa k tématu nové definice SI na Wikimedia Commons