Ortogonální funkce

V matematice o dvou funkcích ${\displaystyle f(x)}$ a ${\displaystyle g(x)}$ řekneme, že jsou ortogonální, pokud jsou splněny tyto podmínky

• ${\displaystyle f(x)}$ a ${\displaystyle g(x)}$ patří do nějakého prostoru funkcí, což je vektorový prostor s bilineární formou
• definičním oborem prostoru funkcí je nějaký interval
• ${\displaystyle f\neq g}$
• existuje bilineání forma definovaná jako integrál součinu funkcí na tomto intervalu:

  ${\displaystyle \langle f,g\rangle =\int {\overline {f(x)}}g(x)\,dx.}$

• ${\displaystyle \langle f,\,g\rangle =0}$

Ortogonální funkce mohou tvořit nekonečnou bázi prostoru funkcí s podobnými vlastnostmi jako má báze vektorů v konečněrozměrném prostoru. Výše uvedený integrál je konceptuálně ekvivalentem skalárního součinu vektorů; dva vektory jsou vzájemně nezávislé (ortogonální), pokud je jejich skalární součin nulový.

Předpokládejme, že ${\displaystyle \{f_{0},f_{1},\ldots \}}$ je posloupnost ortogonálních funkcí s nenulovými L²-normami ${\textstyle \left\|f_{n}\right\|_{2}={\sqrt {\langle f_{n},f_{n}\rangle }}=\left(\int f_{n}^{2}\ dx\right)^{\frac {1}{2}}}$. Pak posloupnost ${\displaystyle \left\{f_{n}/\left\|f_{n}\right\|_{2}\right\}}$ tvořená funkcemi s L²-normou jedna tvoří ortonormální posloupnost. Aby bylo možné definovat L²-normu, musí být integrál omezený, což vyžaduje, aby funkce byly integrovatelné na čtverci.

Trigonometrické funkce

Několik sad ortogonálních funkcí se používá jako báze pro aproximaci funkcí. Například sinové funkce sin nx a sin mx jsou ortogonální na intervalu ${\displaystyle x\in (-\pi ,\pi ),}$ pokud ${\displaystyle m\neq n}$ a n a m jsou kladná celá čísla. Pak

${\displaystyle 2\sin \left(mx\right)\sin \left(nx\right)=\cos \left(\left(m-n\right)x\right)-\cos \left(\left(m+n\right)x\right),}$

a integrál součinu dvou funkcí sinus bude mít nulovou hodnotu.^[1] Složením těchto ortogonálních funkcí s kosinovými funkcemi vzniknou trigonometrické polynomy, které lze použít pro aproximaci libovolné funkce na daném intervalu pomocí Fourierovy řady.

Polynomy

Pokud vyjdeme od posloupnosti monomů ${\displaystyle \left\{1,x,x^{2},\dots \right\}}$ na intervalu ${\displaystyle \langle -1,1\rangle }$ a použijeme Gramovu–Schmidtovu ortogonalizaci, dostaneme posloupnost Legendrových polynomů. Jiným systémem ortogonálních polynomů jsou přidružené Legendrovy polynomy.

Při studiu ortogonálních polynomů hrají důležitou roli váhové funkce ${\displaystyle w(x),}$ které se vyskytují v bilineární formě:

${\displaystyle \langle f,g\rangle =\int w(x)f(x)g(x)\,dx.}$

Pro Laguerrovy polynomy na ${\displaystyle (0,\infty )}$ je váhová funkce ${\displaystyle w(x)=e^{-x}}$.

Fyzikové i teoretici v teorii pravděpodobnosti používají Hermitovy polynomy na intervalu ${\displaystyle (-\infty ,\infty )}$ s váhovou funkcí ${\displaystyle w(x)=e^{-x^{2}}}$ nebo ${\displaystyle w(x)=e^{-x^{2}/2}}$.

Čebyševovy polynomy jsou definovány na intervalu ${\displaystyle \langle -1,1\rangle }$ a používají váhové funkce ${\textstyle w(x)={\frac {1}{\sqrt {1-x^{2}}}}}$ nebo ${\textstyle w(x)={\sqrt {1-x^{2}}}}$.

Zernikeovy polynomy jsou definovány na jednotkovém kruhu a mají ortogonální jak radiální tak angulární složky.

Binární-hodnocený funkce

Walshovy funkce a Haarovy vlnky jsou příkladem ortogonálních funkcí s diskrétním oborem hodnot.

Racionální funkce

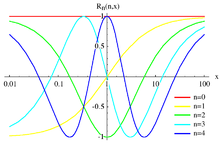
Legendrovy a Čebyševovy polynomy jsou posloupnosti ortogonálních funkcí na intervalu ${\displaystyle \langle -1,1\rangle .}$ Někdy jsou potřeba posloupnosti ortogonálních funkcí na intervalu ${\displaystyle \langle 0,\infty )}$. V tomto případě je pohodlné transformovat argument do intervalu ${\displaystyle \langle -1,1\rangle }$ použitím Cayleyovy transformace. Tento postup vede k rodině racionálních ortogonálních funkcí, které se nazývají Legendrovy racionální funkce a Čebyševovy racionální funkce.

V diferenciálních rovnicích

Řešení lineární diferenciální rovnice s okrajovými podmínkami lze často zapsat jako vážený součet ortogonálních funkcí, které jsou řešením této rovnice (nazývaných také vlastní funkce), což vede k zobecněným Fourierovým řadám.

Odkazy

Reference

V tomto článku byl použit překlad textu z článku Orthogonal functions na anglické Wikipedii.

Literatura

• ARFKEN, George B.; WEBER, Hans J., 2005. Mathematical Methods for Physicists. 6. vyd. [s.l.]: Academic Press. Kapitola 10: Sturm-Liouville Theory — Orthogonal Functions. 
• PRICE, Justin J., 1975. Topics in orthogonal functions. American Mathematical Monthly. Roč. 82, s. 594–609. Dostupné online. DOI 10.2307/2319690. 
• SANSONE, Giovanni, 1959. Orthogonal Functions. [s.l.]: Interscience Publishers. 
• ZYGMUND, Antoni, 1935. Trigonometrical series. [s.l.]: University of Warsaw. 

Související články

• Vlastní vektory a vlastní čísla
• Hilbertův prostor
• Karhunenova–Loèvova věta
• Lauricellova věta
• Wannierovy funkce

Externí odkazy

• Ortogonal Functions na MathWorld.