Přechodnice
Přechodnice se využívá v dopravním stavitelství na pozemních komunikacích a železničních (tramvajových) tratích. Zajišťuje plynulý přechod vozidla z přímého směru do oblouku. Osa komunikace je v půdoryse tvořena křivkou proměnné křivosti umožňující plynulý přechod mezi úseky trasy s různou křivostí. Nejčastěji mezi přímým úsekem, jehož křivost je nulová, a obloukem, jehož křivost je rovna převrácené hodnotě jeho poloměru, ale i mezi oblouky různých poloměrů.
Nejlépe si přechodnici můžeme představit na silnici. Když jedeme po přímé, máme volant v základní poloze. Když se blíží směrový oblouk (hovorově zatáčka), otáčíme volantem, dokud se kola vozidla nenatočí tak, aby vozidlo projelo obloukem. Při průjezdu obloukem máme volant v konstantní poloze, vyplývající z poloměru oblouku. Doba, v níž otáčíme volantem, odpovídá jízdě po přechodnici. Proto se také křivce – klotoidě, která se v ČR na silnicích používá, dříve říkalo volantová křivka, neboť se nejlépe přibližuje ideální stopě vozidla vjíždějícího do oblouku.
Ve světě se jako přechodnice používá řada křivek. V ČR se používá:
- na železnicích kubická parabola a podle nové normy klotoida
- na silnicích klotoida
- na vodních tocích Bernoulliho lemniskáta
Na železničních tratích, je-li v oblouku zřízeno převýšení vnější kolejnice, se do úseku přechodnice umisťuje vzestupnice.
Související články
Externí odkazy
Obrázky, zvuky či videa k tématu přechodnice na Wikimedia Commons - (česky) Popis jednotlivých typů přechodnic[nedostupný zdroj]
Média použitá na této stránce
Autor:
- Easement_Curve.png: Ling Kah Jai
- derivative work: InverseHypercube
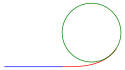
This is an example of a red easement (transition) curve between a blue straight line and a green circular arc. The circular arc is supposed to start at the end of the red easement curve. However, it is drawn as a full circle here.
Sage source code:
var('t')
p = integral(taylor(cos(t^2),t, 0, 12), t)
q = integral(taylor(sin(t^2),t, 0, 12), t)
x1 = p.subs(t = 1)
y1 = q.subs(t = 1)
R = 0.5
x2 = x1 - R*sin(1.0)
y2 = y1 + R*cos(1.0)
r1 = parametric_plot([p, q], (t, 0, 1), color = 'red')
r2 = line([(-1.0, 0), (0,0)], rgbcolor = 'blue')
r3 = circle((x2, y2), R, rgbcolor = 'green')
show(r1 + r2 + r3, aspect_ratio = 1, axes=false)