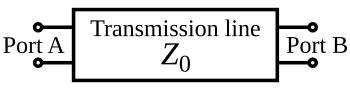
Přenosové vedení

Přenosové vedení je v telekomunikacích a v elektrotechnice speciální kabel nebo jiná struktura vhodná pro přenos elektromagnetických vln uzavřeným způsobem. Termín přenosové vedení se používá pro vedení tak dlouhá, aby bylo nutné brát v úvahu vlnovou povahu přenosu. Ta se projevuje zvláště v oboru radiotechniky, protože použití krátkých vlnových délek znamená, že vlnové jevy se projevují již na malých vzdálenostech (v závislosti na frekvenci to mohou být i milimetry). Teorie přenosových vedení však byla historicky vyvinuta pro vysvětlení jevů, ke kterým dochází u velmi dlouhých telegrafních vedení, zvláště u podmořských telegrafních kabelů.

Přenosová vedení se používají např. pro propojení rádiového vysílače nebo přijímače s anténou (tzv. anténní vedení nebo napáječ), pro šíření signálu kabelové televize, k přenosu telefonních hovorů mezi telefonními ústřednami, pro přenos datových signálů v počítačových sítích a u vysokorychlostních počítačových sběrnic. Při konstrukci zařízení pro kmitočty v pásmu UHF nebo vyšších pásmech se krátké úseky přenosového vedení, obvykle ve formě tištěných rovinných vedení, uspořádané do určitých vzorků často používají také pro vytváření různých obvodů, např. filtrů. Tyto obvody, známé jako obvody s rozloženými parametry, jsou alternativou k tradičním obvodům, v nichž jsou kapacity a indukčnosti realizovány samostatnými (soustředěnými) kondenzátory a cívkami.

Běžné elektrické kabely postačují pro přenos nízkofrekvenčního střídavého proudu, který např. v elektrické síti mění směr 100krát za sekundu (v USA 120krát), a pro přenos audio signálů. Pro přenos vysokofrekvenčních signálů od asi 30 kHz je však nelze použít,^[1] protože při těchto kmitočtech dochází k vyzařování energie z kabelu v podobě rádiových vln, což způsobuje výkonové ztráty. Čím vyšší je frekvence elektromagnetických vln, které se přenášejí vedením, tím kratší je vlnová délka vlnění. Použití speciálního přenosového vedení je nezbytné, pokud vlnová délka přenášené frekvence je tak malá, že délka kabelu je významnou částí vlnové délky. Vysokofrekvenční proudy mají také tendenci se odrážet od diskontinuit vedení, např. konektorů a spojů, a vracet se vedením zpátky ke zdroji.^[1][2] Tyto odrazy brání signálu dosáhnout cíle. Přenosová vedení proto používají specializované konstrukce a impedanční přizpůsobení, aby při přenosu vysokofrekvenčních signálů nedocházelo ke ztrátám energie a odrazům. Význačným rysem většiny přenosových vedení je, že po celé délce mají stejný průřez, díky čemuž mají konstantní impedanci nazývanou charakteristická impedance,^[2][3][4] která zabraňuje odrazům. Jako přenosová vedení se používají symetrická vedení (žebříčková vedení, kroucená dvojlinka), koaxiální kabely, a rovinná přenosová vedení např. pásková vedení a mikropásky.^[5][6]

Na mikrovlnných a vyšších frekvencích se ztráty výkonu při přenosu vedením stávají příliš velkými, a proto se pro přenos takových signálů používají vlnovody,^[1] které fungují jako „trubky“, které vymezují směr šíření a vedou elektromagnetické vlny.^[6] Vlnovody lze považovat za jeden z druhů přenosového vedení;^[6] v tomto článku však popisovány nejsou. Při ještě vyšších frekvencích, v terahertzových pásmech, pro infračervené záření a viditelné světlo, se i vlnovody stávají ztrátovými, a pro přenos elektromagnetických vln těchto délek se používají optické metody – optická vlákna, příp. čočky a zrcadla.^[6]

Matematická analýza chování elektrických přenosových vedení vycházela z prací Jamese Clerka Maxwella, lorda Kelvina, a Olivera Heavisidea. V roce 1855 lord Kelvin formuloval difuzní model proudu v podmořském kabelu. Model správně predikoval neuvěřitelně špatnou výkonnost transatlantického podmořského telegrafního kabelu zprovozněného roku 1858. V roce 1885 Heaviside publikoval první odborné články popisující jeho analýzu šíření signálu kabely a moderní tvar telegrafní rovnice.^[7]

Pro účely analýzy lze elektrické přenosové vedení modelovat jako dvojbran (někdy nazývaný také kvadripól):

V nejjednodušším případě předpokládáme, že vedení je lineární, což znamená, že, pokud nedochází k odrazům, komplexní napětí na obou portech je úměrné komplexnímu proudu do něj tekoucího, a o portech se předpokládá, že jsou zaměnitelné. Pokud přenosové vedení je homogenní po své délce, pak jeho chování je z větší části popsáno jediným parametrem nazývaným charakteristická impedance, značeným Z₀. Je to poměr komplexního napětí dané vlny ku komplexnímu proudu této vlny v libovolném bodě na vedení. Typické hodnoty Z₀ jsou 50 nebo 75 ohmů pro koaxiální kabel, asi 100 ohmů pro vodiče s kroucenou dvojlinkou, a asi 300 ohmů pro televizní dvojlinku používanou pro rádiovou komunikaci.

Při přenosu energie přenosovým vedením, je obvykle žádoucí, aby co nejvíce energie bylo přeneseno do zátěže a co nejméně energie bylo odraženo zpátky ke zdroji. To lze zajistit, pokud je zatěžovací impedance rovna Z₀; v tomto případě říkáme, že přenosové vedení je impedančně přizpůsobené.

Část energie, která je přivedena do vedení, se ztratí kvůli odporu vedení. Tento vliv se nazývá ohmické nebo rezistivní ztráty (viz Jouleovo teplo). Při vysokých frekvencích začne být významný jiný vliv nazývaný dielektrické ztráty, které se přičítají k ohmickým ztrátám. Příčinou dielektrických ztrát je absorpce energie střídavého elektrického pole izolačním materiálem vedení a jeho přeměna na teplo (viz dielektrický ohřev). Přenosové vedení lze modelovat sériově zapojeným odporem (R) a indukčností (L) a paralelně zapojenou kapacitou (C) a konduktancí (G). Odpor a konduktance způsobují ztráty ve vedení.

Celková ztráta energie v přenosovém vedení se často uvádí v decibelech na metr (dB/m), a obvykle závisí na frekvenci signálu. Výrobci často poskytují tabulku ukazující ztráty v dB/m pro různé frekvence. Ztráta 3 dB odpovídá přibližně poloviční energii (případně výkonu).

Vysokofrekvenční přenosová vedení lze definovat jako vedení určená k přenosu elektromagnetických vln, jejichž vlnové délky jsou kratší než nebo srovnatelné s délkou vedení. Za těchto podmínek již aproximace užitečné pro výpočty na nižších frekvencích nejsou přesné. K tomu často dochází u rádiových, mikrovlnných a optických signálů, optických filtrů s kovovými oky a u signálů, se kterými pracují vysokorychlostní digitální obvody.

Telegrafní rovnice je dvojice lineárních diferenciálních rovnic, které popisují elektrické napětí (${\displaystyle V}$) a proud (${\displaystyle I}$) na elektrickém přenosovém vedení v závislosti na místě a čase. Rovnici vytvořil Oliver Heaviside pro svůj model přenosového vedení založený na Maxwellových rovnicích.

Model přenosového vedení je příkladem obvodu s rozloženými parametry. Přenosové vedení je tvořeno nekonečnou řadou elementárních dvojbranových prvků, z nichž každý reprezentuje infinitizimálně krátký úsek přenosového vedení:

• Distribuovaný odpor ${\displaystyle R}$ vodiče je reprezentována sériovým rezistorem (s hodnotou v Ohmech na jednotku délky).
• Distribuovaná indukčnost ${\displaystyle L}$ (kvůli Magnetické pole okolo vodiče, vlastní indukčnost, atd.) je reprezentována sériově zapojenou cívkou (s indukčností udávanou v Henry na jednotku délky).
• Kapacitance ${\displaystyle C}$ mezi oběma vodiči je reprezentována bočníkovým kondenzátorem (s hodnotou ve Faradech na jednotku délky).
• Konduktance ${\displaystyle G}$ dielektrického materiálu oddělujícího oba vodiče je reprezentována bočníkovým rezistorem mezi signálovým a zpětným vodičem (s hodnotou v Siemensech na jednotku délky).

Model sestává z nekonečné řady prvků uvedených na obrázku, a hodnoty součástek jsou zadané na jednotku délky, takže obraz součástek není zcela přesný. ${\displaystyle R}$, ${\displaystyle L}$, ${\displaystyle C}$, a ${\displaystyle G}$ mohou také záviset na frekvenci. Používá se alternativní značení ${\displaystyle R'}$, ${\displaystyle L'}$, ${\displaystyle C'}$ a ${\displaystyle G'}$ pro zdůraznění, že jde o měrné jednotky vztažené na jednotku délky. Těmto hodnotám se také říká primární konstanty vedení, zatímco sekundárními konstantami vedení je konstanta šíření, konstanta útlumu a fázová konstanta.

Ve frekvenční doméně lze napětí na vedení ${\displaystyle V(x)}$ a proud ${\displaystyle I(x)}$ tekoucí vedením vyjádřit rovnicemi

${\displaystyle {\frac {\partial V(x)}{\partial x}}=-(R+j\,\omega \,L)\,I(x)}$

${\displaystyle {\frac {\partial I(x)}{\partial x}}=-(G+j\,\omega \,C)\,V(x)~\,.}$

kde ω je úhlová frekvence a j imaginární jednotka.

Pokud jsou prvky ${\displaystyle R}$ a ${\displaystyle G}$ zanedbatelně malé, přenosové vedení lze považovat za bezztrátovou strukturu. V tomto hypotetickém případě závisí model pouze na prvcích ${\displaystyle L}$ a ${\displaystyle C}$, což značně zjednodušuje analýzu. Pro bezztrátové přenosové vedení mají telegrafní rovnice druhého řádu pro ustálený stav tvar

${\displaystyle {\frac {\partial ^{2}V(x)}{\partial x^{2}}}+\omega ^{2}L\,C\,V(x)=0}$

${\displaystyle {\frac {\partial ^{2}I(x)}{\partial x^{2}}}+\omega ^{2}L\,C\,I(x)=0~\,.}$

Jde o vlnové rovnice, jejichž řešením jsou rovinné vlny se stejnou rychlostí šíření v dopředném i zpětném směru. Jejich fyzikální význam je, že elektromagnetické vlny se šíří přenosovým vedením, a obecně existuje odražená složka, která interferuje s původním signálem. Tyto rovnice jsou základem teorie přenosového vedení.

V obecném případě jsou zahrnuty ztrátové členy ${\displaystyle R}$ a ${\displaystyle G}$, a telegrafní rovnice bude mít tvar

${\displaystyle {\frac {\partial ^{2}V(x)}{\partial x^{2}}}=\gamma ^{2}V(x)\,}$

${\displaystyle {\frac {\partial ^{2}I(x)}{\partial x^{2}}}=\gamma ^{2}I(x)\,}$

kde ${\displaystyle \gamma }$ je (komplexní) konstanta šíření. Tyto rovnice jsou základem teorie přenosového vedení. Existují také vlnové rovnice, jejichž řešení je podobné speciálnímu případu, jsou však kombinací sinů a kosinů s členy reprezentujícími exponenciální pokles. Řešení pro konstantu šíření ${\displaystyle \gamma }$ vyjádřenou pomocí primárních parametrů ${\displaystyle R}$, ${\displaystyle L}$, ${\displaystyle G}$, a ${\displaystyle C}$ je

${\displaystyle \gamma ={\sqrt {(R+j\,\omega \,L)(G+j\,\omega \,C)\,}},}$

přičemž charakteristickou impedanci lze vyjádřit vzorcem

${\displaystyle Z_{0}={\sqrt {{\frac {R+j\,\omega \,L}{G+j\,\omega \,C}}\,}}~\,.}$

Řešeními pro ${\displaystyle V(x)}$ a ${\displaystyle I(x)}$ jsou:

${\displaystyle V(x)=V_{(+)}e^{-\gamma \,x}+V_{(-)}e^{+\gamma \,x}\,}$

${\displaystyle I(x)={\frac {1}{Z_{0}}}\,\left(V_{(+)}e^{-\gamma \,x}-V_{(-)}e^{+\gamma \,x}\right)~\,.}$

Konstanty ${\displaystyle V_{(\pm )}}$ je třeba určit z okrajových podmínek. Pro napěťový impuls ${\displaystyle V_{\mathrm {in} }(t)\,}$ začínající v čase ${\displaystyle x=0,}$ který se šíří ve směru kladné poloosy osy ${\displaystyle x}$ lze přenášený impuls ${\displaystyle V_{\mathrm {out} }(x,t)\,}$ na pozici ${\displaystyle x}$ získat aplikací Fourierovy transformace ${\displaystyle {\tilde {V}}(\omega )}$ z ${\displaystyle V_{\mathrm {in} }(t)\,}$, zeslabením každé frekvenční složky o faktor ${\displaystyle e^{-\operatorname {Re} (\gamma )\,x}\,}$, posunutím fáze o ${\displaystyle -\operatorname {Im} (\gamma )\,x\,}$ a použitím inverzní Fourierovy transformace. Reálnou a imaginární část ${\displaystyle \gamma }$ lze vypočítat podle vzorců

${\displaystyle \operatorname {Re} (\gamma )=\alpha =(a^{2}+b^{2})^{1/4}\cos(\psi )\,}$

${\displaystyle \operatorname {Im} (\gamma )=\beta =(a^{2}+b^{2})^{1/4}\sin(\psi )\,}$

kde

${\displaystyle a~\equiv ~R\,G\,-\omega ^{2}L\,C\ ~=~\omega ^{2}L\,C\,\left[\left({\frac {R}{\omega L}}\right)\left({\frac {G}{\omega C}}\right)-1\right]}$

${\displaystyle b~\equiv ~\omega \,C\,R+\omega \,L\,G~=~\omega ^{2}L\,C\,\left({\frac {R}{\omega \,L}}+{\frac {G}{\omega \,C}}\right)}$

Výrazy na pravých stranách jsou definované, pokud ani ${\displaystyle L}$, ani ${\displaystyle C}$, ani ${\displaystyle \omega }$ není nula, a

${\displaystyle \psi ~\equiv ~{\tfrac {1}{2}}\operatorname {atan2} (b,a)\,}$

kde atan2 je všude definovaná funkce arkus tangens se dvěma parametry; jsou-li oba její argumenty nulové, je její hodnota 0.

Komplexní druhou odmocninu lze také vypočítat algebraicky:

${\displaystyle \alpha ={\frac {\pm b}{\sqrt {2\left(-a+{\sqrt {a^{2}+b^{2}}}\right)~}}},}$

a

${\displaystyle \beta =\pm {\sqrt {{\tfrac {1}{2}}\left(-a+{\sqrt {a^{2}+b^{2}}}\right)~}},}$

přičemž výběr znaménka závisí na směru pohybu vlnění vedením. (Parametr a je obvykle záporný, protože ${\displaystyle G}$, resp. ${\displaystyle R}$ jsou typicky mnohem menší než ${\displaystyle \omega C}$, resp. ${\displaystyle \omega L}$, takže −a je obvykle kladné. b je vždy kladné.)

Pro malé ztráty a vysoké frekvence, když ${\displaystyle {\tfrac {R}{\omega \,L}}\ll 1}$ a ${\displaystyle {\tfrac {G}{\omega \,C}}\ll 1}$, lze obecnou rovnici zjednodušit:

${\displaystyle \operatorname {Re} (\gamma )=\alpha \approx {\tfrac {1}{2}}{\sqrt {L\,C\,}}\,\left({\frac {R}{L}}+{\frac {G}{C}}\right)\,}$

${\displaystyle \operatorname {Im} (\gamma )=\beta \approx \omega \,{\sqrt {L\,C\,}}~.\,}$

Protože posun fáze o ${\displaystyle -\omega \,\delta }$ je ekvivalentní s časovým zpožděním ${\displaystyle \delta }$, lze ${\displaystyle V_{out}(t)}$ jednoduše vypočítat jako

${\displaystyle V_{\mathrm {out} }(x,t)\approx V_{\mathrm {in} }(t-{\sqrt {L\,C\,}}\,x)\,e^{-{\tfrac {1}{2}}{\sqrt {L\,C\,}}\,\left({\frac {R}{L}}+{\frac {G}{C}}\right)\,x}.\,}$

Aby nedocházelo ke zkreslení signálu disperzí, musí být splněna Heavisideova podmínka:

${\displaystyle {\frac {G}{C}}={\frac {R}{L}}}$

Charakteristická impedance ${\displaystyle Z_{0}}$ přenosového vedení je poměr amplitudy jediné napěťové vlny k proudové vlně. Protože na většině přenosových vedení se objevují také odražené vlny, charakteristická impedance obecně není tou impedancí, kterou lze změřit na vedení.

Impedanci změřenou v určité vzdálenosti ${\displaystyle \ell }$ od impedance zátěže ${\displaystyle Z_{\mathrm {L} }}$ lze vyjádřit vzorcem

${\displaystyle Z_{\mathrm {in} }\left(\ell \right)={\frac {V(\ell )}{I(\ell )}}=Z_{0}{\frac {1+{\mathit {\Gamma }}_{\mathrm {L} }e^{-2\gamma \ell }}{1-{\mathit {\Gamma }}_{\mathrm {L} }e^{-2\gamma \ell }}}}$,

kde ${\displaystyle \gamma }$ je konstanta šíření a ${\displaystyle {\mathit {\Gamma }}_{\mathrm {L} }={\frac {\,Z_{\mathrm {L} }-Z_{0}\,}{Z_{\mathrm {L} }+Z_{0}}}}$ je napěťový činitel odrazu změřený na straně zátěže přenosového vedení. Výše uvedený vzorec lze také upravit, aby vyjadřoval vstupní impedanci pomocí zatěžovací impedance místo napěťového činitel odrazu zátěže:

${\displaystyle Z_{\mathrm {in} }(\ell )=Z_{0}\,{\frac {Z_{\mathrm {L} }+Z_{0}\operatorname {tgh} \left(\gamma \ell \right)}{Z_{0}+Z_{\mathrm {L} }\,\operatorname {tgh} \left(\gamma \ell \right)}}}$.

Pro bezztrátové přenosové vedení je konstanta šíření čistě imaginární, ${\displaystyle \gamma =j\,\beta }$, takže výše uvedené vzorce lze přepsat do tvaru

${\displaystyle Z_{\mathrm {in} }(\ell )=Z_{0}{\frac {Z_{\mathrm {L} }+j\,Z_{0}\,\operatorname {tg} (\beta \ell )}{Z_{0}+j\,Z_{\mathrm {L} }\operatorname {tg} (\beta \ell )}}}$

kde ${\displaystyle \beta ={\frac {\,2\pi \,}{\lambda }}}$ je vlnové číslo.

Při výpočtu ${\displaystyle \beta ,}$ je vlnová délka obecně jiná na přenosovém vedení, než by byla ve volném prostoru. Při provádění výpočtů musí být brán v úvahu činitel zkrácení.

Pro speciální případ kde ${\displaystyle \beta \,\ell =n\,\pi }$, kde n je celé číslo (s významem, že délka vedení je násobkem poloviny vlnové délky), se výraz zjednoduší na impedanci zátěže, tedy

${\displaystyle Z_{\mathrm {in} }=Z_{\mathrm {L} }\,}$

pro všechna ${\displaystyle n\,.}$ To platí i pro případ, kdy ${\displaystyle n=0}$, tedy když délka přenosového vedení je zanedbatelně malá vůči vlnové délce. Fyzikální význam je, že přenosové vedení lze v tomto případě ignorovat (tj. považovat za vodič).

Pokud je délka vedení je rovna čtvrtině vlnové délky nebo jejím lichým násobkům, bude vstupní impedance

${\displaystyle Z_{\mathrm {in} }={\frac {Z_{0}^{2}}{Z_{\mathrm {L} }}}~\,.}$

Jiným speciálním případem je, když impedance zátěže je rovna charakteristické impedanci vedení (tj. zátěž a vedení jsou vzájemně přizpůsobené). V tomto případě je impedance rovna charakteristické impedanci vedení, tj.

${\displaystyle Z_{\mathrm {in} }=Z_{\mathrm {L} }=Z_{0}\,}$

pro libovolné ${\displaystyle \ell }$ a libovolné ${\displaystyle \lambda }$.

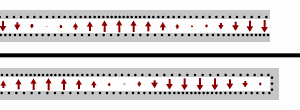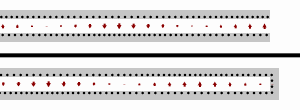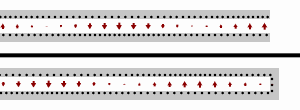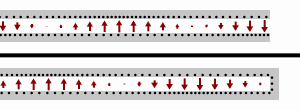
V případě že zátěž je tvořena zkratem (tj. ${\displaystyle Z_{\mathrm {L} }=0}$), vstupní impedance je čistě imaginární a pro periodickou funkci pozice a vlnové délky (frekvence) platí

${\displaystyle Z_{\mathrm {in} }(\ell )=j\,Z_{0}\,\operatorname {tg} (\beta \ell ).\,}$

Pro případ otevřené zátěže (tj. ${\displaystyle Z_{\mathrm {L} }=\infty }$), vstupní impedance je také imaginární a platí

${\displaystyle Z_{\mathrm {in} }(\ell )=-j\,Z_{0}\operatorname {cotg} (\beta \ell ).\,}$

Koaxiální vedení uzavírá prakticky veškeré elektromagnetické vlnění v prostoru kabelu. Koaxiální vedení lze proto ohýbat (v rámci povolených limitů) bez záporných efektů, a může být umístěno na vodivém podkladu bez toho, že by docházelo k indukování nežádoucích proudů. Pro vysokofrekvenční aplikace do kmitočtu několika málo gigahertzů se vlnění šíří pouze v příčném elektrickém a magnetickém vidu (anglicky transverse electric and magnetic mode, TEM), což znamená, že elektrická i magnetická složka jsou kolmé ke směru šíření (elektrické pole je radiální, a magnetické pole je obvodové, cirkumferenciální). Avšak při frekvencích, kdy je vlnová délka (v dielektriku) je výrazně kratší než obvod kabelu, se mohou objevit i jiné příčné vidy. Tyto vidy lze rozdělit na dvě skupiny, příčné elektrické (TE) a příčné magnetické (TM) vlnovodné vidy. Pokud může existovat více než jeden vid, mohou ohyby a jiné nepravidelnosti v geometrii kabelu způsobit přenos výkonu z jednoho vidu do druhého.

Nejběžnějším použitím koaxiálních kabelů je přenos televizních a jiných signálů s šířkou pásma několik megahertzů. V polovině 20. století se také používaly pro dálková telefonní vedení.

Rovinná přenosová vedení jsou přenosová vedení s vodiči nebo v některých případech dielektrickými pásky, které mají tvar plochého pásu. Používají se pro propojení součástek na deskách plošných spojů a v integrovaných obvodech pracujících na mikrovlnných frekvencích, protože rovinný typ lze snadno vyrábět metodami používanými pro výrobu těchto součástek. Existuje několik forem rovinných přenosových vedení.

Mikropáskové vedení (anglicky microstrip) používá tenký plochý vodič, který je rovnoběžný se zemní rovinou. Mikropásky mohou mít podobu proužku mědi na jedné straně plošného spoje nebo keramického substrátu, přičemž opačná strana je spojena se zemní rovinou. Šířka pásku, tloušťka izolační vrstvy (plošného spoje nebo keramiky) a dielektrický konstanta izolační vrstvy určují charakteristickou impedanci. Na rozdíl od koaxiální kabelu jsou mikropásky otevřenou strukturou.

Páskové vedení (anglicky stripline) je tvořeno plochým proužkem kovu, který je umístěn mezi dvě rovnoběžné zemní roviny. Izolační materiál substrátu tvoří dielektrikum. Šířka pásku, tloušťka substrátu a relativní permitivita substrátu určují charakteristickou impedanci přenosového vedení tvořeného páskem.

Koplanární vlnovod sestává ze středového proužku a dvou sousedících vnějších vodičů, které všechny mají plochou strukturu, které jsou umístěna na stejném izolačním substrátu a jsou tedy umístěné ve stejné rovině („koplanární“). Šířka středového vodiče, vzdálenost mezi vnitřním a vnějšími vodiči, a relativní permitivita substrátu určuje charakteristickou impedanci koplanárního přenosového vedení.

Vyvážené vedení je přenosové vedení tvořené dvěma vodiči stejného typu a se stejnou impedancí vůči zemi a jiným obvodům. Existuje mnoho formátů vyvážených vedení, k nejběžnějším patří kroucená dvojlinka, star quad a dvojlinka.

Kroucené páry se často používají pro pozemní Telefon komunikace. V takových kabelech, mnoho páry jsou sdružený dohromady v jednom kabelu, od dvou do několika tisíc.^[8] Formát se také používá pro data síť rozdělení v budovy, ale kabel je nákladnější, protože parametry přenosového vedení jsou striktně řízený.

Star quad je čtyřžilový kabel, ve kterém jsou všechny čtyři vodiče stočené dohromady kolem osy kabelu. Může se používat pro dva obvody, např. v podobě čtyřdrátových telefonních okruhů a jiných telekomunikačních aplikací. V této konfiguraci každý pár používá dva nesousedící vodiče. Jindy používá se pro jediné symetrické vedení signálu, např. pro audio aplikace a dvoudrátové telefonní okruhy. V této konfiguraci jsou dva nesousedící vodiče na obou koncích kabelu spolu propojeny, stejně jako druhé dva vodiče.

Při použití pro dva okruhy má nižší přeslechy než kabely se dvěma samostatnými kroucenými páry.

Při použití pro jeden symetrický okruh je magnetické rušení zachycené kabelem přijato jako prakticky dokonalý soufázový signál, který lze snadno odstranit vazebními transformátory.

Kombinace zkroucení, symetrické signalizace a čtyřpólového vzoru poskytuje vynikající odolnost proti šumu, což je výhodné zejména pro aplikace s nízkými úrovněmi signálu, jako jsou mikrofonní kabely, a to i při instalaci velmi blízko napájecího kabelu.^{[9][10][11][12][13]} Nevýhodou star quad je, že má při propojení dvojic vodičů typicky dvojnásobnou kapacitanci než obdobný dvouvodičový kroucený stíněný audio kabel. Vysoká kapacitance způsobuje větší zkreslení a větší ztráty na vysokých frekvencích se zvětšující se vzdáleností.^[14][15]

Dvojlinka je tvořena dvojicí vodičů vzájemně oddělených souvislým izolátorem. Díky tomu, že jsou vodiče od sebe v konstantní vzdálenosti, je geometrie vedení pevně daná a jeho vlastnosti jsou spolehlivě konzistentní. Dvojlinka má nižší ztráty než koaxiální kabel, protože její charakteristická impedance je obecně vyšší než koaxiálního kabelu, což vede k nižším odporovým ztrátám v důsledku snížení proudu. Je však citlivější na rušení.

Lecherovo vedení má formu symetrických vodičů, které lze používat v UHF pro vytváření rezonančních obvodů. Jde o pohodlný praktický formát, který vyplňuje mezeru mezi součástkami se soustředěnými parametry (používanými v pásmech HF/VHF) a rezonančními dutinami (používanými v pásmech v UHF/SHF).

Nesymetrická vedení se dříve hojně používala pro telegrafii, ale tato forma komunikace již zanikla. Kabely s nesymetrickými vodiči se podobají kabelům s kroucenými páry v tom, že obsahují mnoho žil. Na jeden obvod je však použit pouze jeden vodič a žíly nejsou kroucené. Všechny obvody na téže trase používají společnou cestu pro zpětný proud (zemní zpětné vedení). Na mnoha místech se používá jednovodičové vedení s návratem zemí pro přenos elektrické energie.

Elektrická přenosová vedení se často používají pro přenos vysokofrekvenčních signálů na dlouhé nebo krátké vzdálenosti s minimální výkonovou ztrátou. Známým příkladem je anténní vedení od televizní, satelitní nebo rozhlasové antény k přijímači.

Použitím přenosového vedení může být zkonstruováno množství obvodů – obvody impedančního přizpůsobení, filtry, děliče výkonu a směrové vazebné členy.

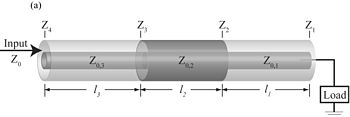
Stupňovité přenosové vedení se používá pro širokopásmové impedanční přizpůsobení. Lze je považovat za několik sériově zapojených segmentů přenosového vedení s charakteristickou impedancí každého jednotlivého prvku ${\displaystyle Z_{\mathrm {0,i} }}$.^[16] Vstupní impedanci lze získat opakovaným použitím řetězové relace

${\displaystyle Z_{\mathrm {i+1} }=Z_{\mathrm {0,i} }\,{\frac {\,Z_{\mathrm {i} }+j\,Z_{\mathrm {0,i} }\,\operatorname {tg} (\beta _{\mathrm {i} }\ell _{\mathrm {i} })\,}{Z_{\mathrm {0,i} }+j\,Z_{\mathrm {i} }\,\operatorname {tg} (\beta _{\mathrm {i} }\ell _{\mathrm {i} })}}\,}$

kde ${\displaystyle \beta _{\mathrm {i} }}$ je vlnový počet ${\displaystyle \mathrm {i} }$-tého segmentu přenosového vedení, ${\displaystyle \ell _{\mathrm {i} }}$ je délka tohoto segmentu a ${\displaystyle Z_{\mathrm {i} }}$ je přední část impedance, která zatěžuje ${\displaystyle \mathrm {i} }$-tý segment.

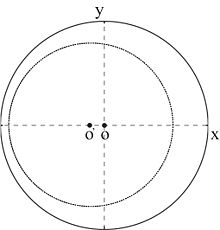
Protože charakteristická impedance každého segmentu přenosového vedení ${\displaystyle Z_{\mathrm {0,i} }}$ je často odlišná od impedance ${\displaystyle Z_{0}}$ čtvrtého, vstupního kabelu (znázorněného pouze šipkou s označením ${\displaystyle Z_{0}}$ na levé straně výše uvedeného schématu), kružnice transformace impedance je posunuta mimo střed podél osy ${\displaystyle x}$ Smithova diagramu, jehož impedanční reprezentace je obvykle normalizována vůči ${\displaystyle Z_{0}}$.

Pokud je zkratované nebo otevřené přenosové vedení vedeno paralelně s vedením používaným pro přenos signálů z bodu A do bodu B, pak bude fungovat jako filtr. Metoda vytváření pahýlů je podobná metodě použití Lecherova vedení pro hrubé měření frekvence, ale funguje obráceně. Jednou z metod doporučených v radiokomunikační příručce Radio Society of Great Britain je vzít délku otevřeného přenosového vedení zapojeného paralelně s napájecím vedením přivádějícím signál z antény. Zkracováním volného konce přenosového vedení lze nalézt minimum síly signálu v přijímači. V tomto uspořádání bude pahýlový filtr potlačovat tuto frekvenci a její liché harmonické; pokud bude volný konec pahýlu zkratován, pak bude potlačovat sudé harmonické.

Použitím více pahýlů lze vytvořit širokopásmové filtry. Je to však poměrně zastaralá technika. Mnohem kompaktnější filtry lze vytvořit jinými metodami např. rezonátory se symetrickým vedením.

Přenosová vedení lze použít jako generátory impulsů. Nabitím přenosového vedení a jeho následným vybíjením do rezistivní zátěže lze získat pravoúhlý impuls, jehož délka odpovídá dvojnásobku elektrické délky vedení, ale o polovičním napětí. Blumleinovo přenosové vedení je podobné zařízení pro vytváření impulsů, které překonává toto omezení. Tato zařízení se někdy používají jako zdroje pulzního výkonu pro radarové vysílače a jiná zařízení.

Teorie šíření zvukových vln je matematicky velmi podobná teorii šíření elektromagnetických vln, proto se techniky z teorie vedení používají pro vytváření struktur pro vedení akustických vln, které se nazývají akustická přenosová vedení.

V tomto článku byl použit překlad textu z článku Transmission line na anglické Wikipedii.

Část tohoto článku používá materiály z Federální Standard 1037C.

• STEINMETZ, Charles Proteus. The natural period of a transmission line and the frequency of lightning discharge therefrom. The Electrical World. 1898-08-27, s. 203–205. 
• GRANT, I.S.; PHILLIPS, W.R. Electromagnetism. 2. vyd. [s.l.]: John Wiley, 1991-08-26. Dostupné online. ISBN 978-0-471-92712-9. 
• ULABY, F.T., 2004. Fundamentals of Applied Electromagnetics. 2004 media. vyd. [s.l.]: Prentice Hall. Dostupné online. ISBN 978-0-13-185089-7. 
• , 1982. Radio communication handbook. [s.l.]: Radio Society of Great Britain. Dostupné online. ISBN 978-0-900612-58-9. Kapitola Chapter 17, s. 20. 
• NAREDO, J.L.; SOUDACK, A.C.; MARTI, J.R. Simulation of transients on transmission lines with corona via the method of characteristics. IEE Proceedings - Generation, Transmission and Distribution. Jan 1995, roč. 142, čís. 1, s. 81. ISSN 1350-2360. DOI 10.1049/ip-gtd:19951488. 
• Honoring of Guglielmo Marconi. In: Annual Dinner of the Institute at the Waldorf-Astoria. New York: American Institute of Electrical Engineers, 1902-01-13. Dostupné online.
• , 2001. Using Transmission Line Equations and Parameters [online]. Avant! Software, June 2001. (Star-Hspice Manual). Dostupné v archivu pořízeném z originálu dne 2005-09-25. 
• CORNILLE, P., 1990. On the propagation of inhomogeneous waves. Journal of Physics D: Applied Physics. Roč. 23, čís. 2, s. 129–135. DOI 10.1088/0022-3727/23/2/001. Bibcode 1990JPhD...23..129C. 
• FARLOW, 1982. Partial Differential Equations for Scientists and Engineers. [s.l.]: J. Wiley and Sons. Dostupné online. ISBN 0-471-08639-8. S. 126. 
• KUPERSHMIDT, Boris A., 1998. Remarks on random evolutions in Hamiltonian representation. J. Nonlinear Math. Phys.. Roč. 5, čís. 4, s. 383–395. DOI 10.2991/jnmp.1998.5.4.10. S2CID 14771417. Bibcode 1998JNMP....5..483K. arXiv math-ph/9810020. Math-ph/9810020. 
• Transmission line matching [online]. Hong Kong Polytechnic University [cit. 2023-05-17]. (High Frequency Circuit Design). Dostupné v archivu pořízeném dne 2011-07-21. EIE403. 
• Wilson, B. Telegrapher's Equations [online]. 2005-10-19. (Connexions). Dostupné v archivu pořízeném z originálu dne 2006-01-09. 
• WÖHLBIER, John Greaton. Modeling and Analysis of a Traveling Wave under Multitone Excitation. Madison, WI, 2000. M.S.. . Dostupné online.
• Wave Propagation along a Transmission Line [online]. Keysight Technologies. (Educational Resources). Dostupné online. ^{[nedostupný zdroj]}
• QIAN, Chunqi; BREY, William W., 2009. Impedance matching with an adjustable, segmented transmission line. Journal of Magnetic Resonance. Roč. 199, čís. 1, s. 104–110. DOI 10.1016/j.jmr.2009.04.005. PMID 19406676. Bibcode 2009JMagR.199..104Q. 

• Umělé přenosové vedení
• Podélné vlnění
• Fázová rychlost
• Reflektometr v časové doméně

• Obrázky, zvuky či videa k tématu přenosové vedení na Wikimedia Commons
• Transmission Line Calculator (Including radiation and surface-wave excitation losses) [online]. Delft, NL: Technická univerzita v Delftu. Dostupné online. 
• Transmission Line Parameter Calculator [online]. Clemson, SC: Clemson University. Dostupné online.