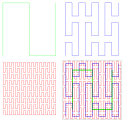
Peanova křivka

Peanova křivka je křivka vyplňující dvourozměný prostor. Objevil a popsal ji italský matematik Giuseppe Peano (1858–1932) v roce 1890, inspirován prací Georga Cantora.

Konstrukce

• první iterace má tvar lomené úsečky; lomené dvakrát na jednu stranu a dvakrát na stranu k ní opačnou
• každá další iterace rozděluje předchozí na 3×3 segmenty, do nichž je vložen základní tvar, transformovaný (t.j. otočený nebo osově převrácený) podle daného vzoru
• je možné zkonstruovat i varianty Peanovy křivky^[1]
• Peanovu křivku lze zkonstruovat rekurzivně s použitím následující „gramatiky“:
  • Nechť P, Q, R, S jsou první iterace Peanovy křivky v těchto směrech:
    • P: ↑ → ↓ →
    • Q: ↑ ← ↓ ←
    • R: ↓ ← ↑ ←
    • S: ↓ → ↑ →
  • V následujících iterací přecházejí:
    • P → ${\displaystyle {\begin{pmatrix}P&S&P\\Q&R&Q\\P&S&P\end{pmatrix}}}$
    • Q → ${\displaystyle {\begin{pmatrix}Q&R&Q\\P&S&P\\Q&R&Q\end{pmatrix}}}$
    • R → ${\displaystyle {\begin{pmatrix}R&Q&R\\S&P&S\\R&Q&R\end{pmatrix}}}$
    • S → ${\displaystyle {\begin{pmatrix}S&P&S\\R&Q&R\\S&P&S\end{pmatrix}}}$
  • Koncové body jsou poté spojeny

Vlastnosti

• podobně jako např. dračí křivka nevyplňuje prostor neomezeně, ale daný první iterací
• je soběpodobná, invariantní vůči měřítku
• v klasické verzi je bodově symetrická podle svého středu
• s každou iterací roste počet nových podsegmentů devítinásobně (3×3)

Odkazy

Reference

Literatura

• Gugenheimer, Heinrich Walter (1963), Differential Geometry, Courier Dover Publications, p. 3, ISBN 978-0-486-15720-7.

Související články

• Křivka vyplňující prostor
• Giuseppe Peano

Externí odkazy

• Obrázky, zvuky či videa k tématu Peanova křivka na Wikimedia Commons
• http://dx.doi.org/10.1007%2FBF01199438