Perturbace (astronomie)
V astronomii jsou perturbace odchylky (poruchy) pohybu hmotného tělesa od keplerovské dráhy (viz Keplerova úloha týkající se pohybu dvou těles) způsobené jinými silami jako je gravitační přitažlivost dalších těles,[1] odpor např. atmosféry a mimostředovou přitažlivost sféroidu nebo jinak nepravidelného tělesa.

Úvod
Studium perturbací začalo s prvními pokusy předpovědět pohyby planet na obloze, i když jejich příčiny zůstávaly v starověku neznámé. Když Newton formuloval pohybové zákony a zákon všeobecné gravitace, aplikoval je na první analýzu perturbací, spoznaje komplexní složitost jejich výpočtu[2]. Od té doby se mnoho velkých matematiků věnovalo souvisejícím problémům kvůli potřebě přesných tabulek pozic Měsíce a planet pro navigaci na moři v 18. a 19. století.
Komplexní pohyby gravitačních perturbací lze rozdělit. Hypotetický pohyb hmotného tělesa v gravitačním poli jednoho dalšího tělesa je s velkou přesností kuželosečka a lze jí lehce popsat metodami geometrie. Nazývá se to problém dvou těles a jeho řešením je nerušená keplerovská dráha. Rozdíly mezi tímto a skutečným pohybem tělesa jsou perturbace způsobené hlavně gravitačními vlivy dalších těles. Pokud uvažujeme pouze jedno další významné těleso, pak perturbační (rušený) pohyb popisuje problém tří těles. Pokud existuje více dalších těles, jde o problém n těles. Analytická řešení (matematické výrazy na predikci pozicí a pohybů v jakémkoli budoucím čase) pro problém dvou a tří těles existuje, ale kromě některých speciálních případů nejsou známa pro problém n těles. Dokonce i problém dvou těles se stane neřešitelným, pokud má jedno z těles nepravidelný tvar.[3]
Většina systémů obsahujících vícenásobné gravitační přitažlivosti prezentuje jedno primární těleso, které je dominantní ve svých vlivech (např. hvězda v případě hvězdy a její planety, nebo planeta v případě planety a jejího satelitu). Gravitační vlivy jiných těles lze uvažovat jako perturbace hypotetického neodchýleného pohybu planety nebo satelitu kolem jeho primárního tělesa.
Matematická analýza
Všeobecné perturbace
V metodách všeobecných perturbací se obecné diferenciální rovnice, buď pohybu nebo změny orbitálních elementů, řeší analyticky obvykle použitím rozvojů řad. Výsledek je obvykle vyjádřen pomocí algebraických a trigonometrických funkcí dráhových elementů daného tělesa a perturbujících těles. Tento postup lze obecně aplikovat na mnoho různých podmínek a není specifický pro nějakou určitou sestavu gravitačních objektů.
Periodická povaha

Ve Sluneční soustavě je většina rušení pohybu jedné planety druhou periodických, složených z malých impulzů vznikajících pokaždé, když se planety přiblíží na svém orbitu. To způsobuje, že tělesa konají pohyby, které jsou periodické nebo kvaziperiodické, např. Měsíc na své silně rušené oběžné dráze, které jsou předmětem teorie lunárního pohybu. Periodicita poruch pohybu Uranu vedla v roce 1846 k objevu Neptunu.
Reference
V tomto článku byl použit překlad textu z článku Perturbation (astronomy) na anglické Wikipedii.
- ↑ Bate, Mueller a White 1971, e.g. ch. 9, p. 385.
- ↑ Newton v roce 1684 napsal: "By reason of the deviation of the Sun from the center of gravity, the centripetal force does not always tend to that immobile center, and hence the planets neither move exactly in ellipses nor revolve twice in the same orbit. Each time a planet revolves it traces a fresh orbit, as in the motion of the Moon, and each orbit depends on the combined motions of all the planets, not to mention the action of all these on each other. But to consider simultaneously all these causes of motion and to define these motions by exact laws admitting of easy calculation exceeds, if I am not mistaken, the force of any human mind." Protože Slunce není Kvůli odchylkám Slunce od těžiště nesměřuje dostředivá síla vždy do tohoto nehybného středu, a proto se planety nepohybují přesně po elipsách ani neobíhají dvakrát po stejné dráze. Při každém oběhu planeta vytyčí novou dráhu, jako je tomu při pohybu Měsíce, a každá dráha závisí na kombinaci pohybů všech planet, nemluvě o jejich vzájemném působení. Uvažovat současně o všech těchto příčinách pohybu a definovat tyto pohyby přesnými zákony umožňujícími snadný výpočet však přesahuje, nemýlím-li se, síly jakékoli lidské mysli. (quoted by Prof G E Smith (Tufts University), in "Three Lectures on the Role of Theory in Science" 1. Closing the loop: Testing Newtonian Gravity, Then and Now); and Prof R F Egerton (Portland State University, Oregon) after quoting the same passage from Newton concluded: "Here, Newton identifies the "many body problem" which remains unsolved analytically." Archivováno 10. 3. 2005 na Wayback Machine.
- ↑ Roy 1988, chapters 6 and 7.
- BATE, Roger R.; MUELLER, Donald D.; WHITE, Jerry E., 1971. Fundamentals of Astrodynamics. New York: Dover Publication. Dostupné online. ISBN 0-486-60061-0.
- MOULTON, Forest Ray, 1914. An Introduction to Celestial Mechanics. 2 revidované. vyd. [s.l.]: Macmillan. Dostupné online.
- ROY, A. E., 1988. Orbital Motion. 3. vyd. [s.l.]: Institute of Physics Publishing. ISBN 0-85274-229-0.
- ANDRLE, Pavel, 1971. Základy nebeské mechaniky. 1. vyd. Praha: Academia. 308 s.
Související články
Média použitá na této stránce
Autor: frankuitaalst from the Gravity Simulator message board., Licence: GPL
Gravity Simulator plot of the changing orbital eccentricity of Mercury, Venus, Earth, and Mars over the next 50,000 years. The 0 point on this plot is 2007-02-01. On going perturbations of the planets by other planets cause small variations in the Kepler orbits. Venus currently has the most circular orbit of the planets, but in 25,000 years Earth will have a more circular (less eccentric) orbit than Venus.
Note were the arrows point as the the Y axis uses two different scales.
Autor: Tfr000 (talk) 20:40, 6 March 2012 (UTC), Licence: CC BY-SA 3.0
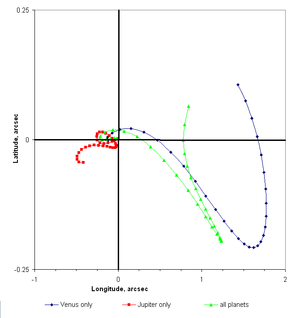
Plot of Mercury's orbital position, with and without perturbations from various other planets; created in MS Excel from author's data.
Autor: Vectorised by User:Sushant savla from the work by Tfr000 (talk), Licence: CC BY-SA 3.0
Moon perturbation diagram