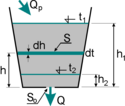
Plnění a prázdnění nádrže

Když do nádrže či nádoby kapalina přitéká a současně z ní odtéká, mohou nastat tři případy:

• nádrž se plní, pokud přítok je větší než odtok,
• nádrž se prázdní, pokud přítok je menší než odtok,
• hladina zůstává konstantní, pokud se přítok právě rovná odtoku, stav je ustálený (viz výtok otvorem).

Přitom jak první, tak druhý stav může za určitých okolností přejít do stavu třetího - ustáleného. Pokud je přítok do nádrže roven nule a odtok je nenulový, nádrž se může pouze prázdnit, a naopak, pokud je odtok z nádrže roven nule a přítok je nenulový, nádrž se může pouze plnit.

Do nádrže přitéká průtok ${\displaystyle Q_{p}}$ [m³s⁻¹] a odtéká průtok ${\displaystyle Q_{o}}$ [m³s⁻¹]. Za čas ${\displaystyle dt}$ [s] tedy přiteče objem ${\displaystyle Q_{p}dt}$ [m³] a odteče objem ${\displaystyle Q_{o}dt}$ [m³]. Rozdíl těchto objemů musí být roven změně objemu v nádrži za tentýž čas. Uvažujme, že nádrž má plochu hladiny ${\displaystyle S}$ [m²] a za čas ${\displaystyle dt}$ se hladina v nádrži změní o ${\displaystyle dh}$ [m], čili objem kapaliny v nádrži se změní o ${\displaystyle Sdh}$ [m³]. Musí tedy platit^[1][2]

${\displaystyle (Q_{p}-Q_{o})dt=Sdh}$

Obvykle nás zajímá, jak dlouho bude trvat než se nádrž naplní či vyprázdní ať již zcela, nebo z určité kóty (nebo polohy hladiny) na jinou, takže

${\displaystyle dt={{Sdh} \over {Q_{p}-Q_{o}}}}$

a integrací této rovnice bude výsledný čas ${\displaystyle t}$ [s] roven

${\displaystyle t=t_{2}-t_{1}=\int _{h_{2}}^{h_{1}}{S \over {Q_{p}-Q_{o}}}dh}$.

Odtok z nádrže uvažujeme jako výtok malým otvorem, nátrubkem nebo potrubím - ve všech těchto případech jej můžeme vyjádřit stejným způsobem jako

${\displaystyle Q_{o}=\mu S_{o}{\sqrt {2gh}}}$

kde ${\displaystyle \mu }$ [-] je součinitel výtoku, ${\displaystyle S_{o}}$ [m²] plocha výtokového otvoru (nátrubku nebo potrubí) a ${\displaystyle h}$ [m] je výška hladiny nad těžištěm výtokového otvoru. Potom tedy bude

${\displaystyle t=t_{2}-t_{1}=\int _{h_{2}}^{h_{1}}{S \over {Q_{p}-Q_{o}}}dh=\int _{h_{2}}^{h_{1}}{S \over {Q_{p}-\mu S_{o}{\sqrt {2gh}}}}dh}$.

Rovnice je analyticky řešitelná pouze pokud přítok ${\displaystyle Q_{p}=konst}$ nebo ${\displaystyle Q_{p}=0}$ a pokud jsme schopni vyjádřit plochu hladiny v nádrži jako funkci polohy hladiny, resp. hloubky - ${\displaystyle S=f(h)}$.

Mějme prismatickou nádrž, jejíž plocha hladiny je ${\displaystyle S}$. Základní diferenciální rovnice bude (viz výše) pro prázdnění (hladina klesá, ${\displaystyle dh<0}$)

${\displaystyle (Q_{p}-Q_{o})dt=Sdh}$

Přítok do nádrže můžeme vyjádřit obdobně jako výtok z nádrže, přičemž uvažujeme totožné parametry (výtokový součinitel a plochu výtokového otvoru) - tento trik podstatně zjednoduší až vůbec umožní výpočet. Přítok tedy bude

${\displaystyle Q_{p}=\mu S_{o}{\sqrt {2gh_{p}}}}$

kde ${\displaystyle h_{p}}$ [m] je tlačná výška, při které by výtok otvorem byl roven přítoku do nádrže, a tedy čas, za který se změní hladina z úrovně ${\displaystyle h_{1}}$ na úroveň ${\displaystyle h_{2}}$ bude

${\displaystyle t=t_{2}-t_{1}=\int _{h_{1}}^{h_{2}}{S \over {Q_{p}-Q_{o}}}dh=\int _{h_{1}}^{h_{2}}{S \over {\mu S_{o}{\sqrt {2g}}({\sqrt {h_{p}}}-{\sqrt {h}})}}dh}$

Protože u prismatické nádoby ${\displaystyle S=konst}$, lze vztah dále upravit:

${\displaystyle t={S \over {\mu S_{o}{\sqrt {2g}}}}\int _{h_{1}}^{h_{2}}{1 \over ({\sqrt {h_{p}}}-{\sqrt {h}})}dh}$.

Po substituci ${\displaystyle y={\sqrt {h_{p}}}-{\sqrt {h}}}$ a integraci dostáváme poměrně složitý výsledný vztah^[1][2]

${\displaystyle t={S \over {\mu S_{o}{\sqrt {2g}}}}\left[{\sqrt {h_{1}}}-{\sqrt {h_{2}}}-{\sqrt {h_{p}}}\ln {{{\sqrt {h_{p}}}-{\sqrt {h_{2}}}} \over {{\sqrt {h_{p}}}-{\sqrt {h_{1}}}}}\right]}$.

Je-li přítok do nádrže nulový (${\displaystyle Q_{p}=0}$), bude

${\displaystyle Q_{o}dt=\mu S_{o}{\sqrt {2gh}}dt=-Sdh}$

a po integraci tedy

${\displaystyle t={{2S} \over {\mu S_{o}{\sqrt {2g}}}}{\Bigl (}{\sqrt {h_{1}}}-{\sqrt {h_{2}}}{\Bigr )}}$.

Označme dobu nutnou k úplnému vyprázdnění nádrže ${\displaystyle T}$ [s]. Při úplném vyprázdnění bude ${\displaystyle h_{2}=0}$ a tedy

${\displaystyle T={{2S{\sqrt {h_{1}}}} \over {\mu S_{o}{\sqrt {2g}}}}}$.

Pokud zlomek rozšíříme ${\displaystyle {\sqrt {h_{1}}}}$, bude

${\displaystyle T={{2Sh_{1}} \over {\mu S_{o}{\sqrt {2gh_{1}}}}}}$

přičemž ${\displaystyle Sh_{1}}$ je počáteční objem kapaliny v nádrži a jmenovatel vyjadřuje ustálený výtok při hladině v úrovni ${\displaystyle h_{1}}$, Zřejmě tedy k úplnému vyprázdnění nádrže bude třeba dvojnásobný čas než je nutný, aby tentýž objem kapaliny vytekl otvorem při ustáleném stavu.

Mějme dvě prismatické nádrže (A a B) o plochách hladiny ${\displaystyle S_{A}}$ [m²] a ${\displaystyle S_{B}}$ [m²], propojené otvorem nebo potrubím s vhodným uzávěrem; propojení ústí do nádrže B pod hladinou kapaliny při jejím nejnižším stavu. Rozdíl hladin mezi nádrží A a nádrží B (tzv. spád) budiž ${\displaystyle H}$ [m]. Otevřeme-li uzávěr, bude kapalina v nádrži A klesat, v nádrži B naopak stoupat, takže rozdíl hladin se bude měnit (zmenšovat), až dojde k vyrovnání hladin.

Propojením o průřezu ${\displaystyle S}$ [m²] za čas ${\displaystyle dt}$ [s] proteče objem kapaliny

${\displaystyle Qdt=\mu S{\sqrt {2gh}}dt}$.

Při propojení otvorem lze součinitel výtoku ${\displaystyle \mu }$ [-] brát běžnou odpovídající hodnotou, pokud je propojení provedeno potrubím, je nutno do součinitele výtoku zahrnout všechny ztráty v příslušném potrubí a součinitel výtoku tedy bude^[1]

${\displaystyle \mu ={1 \over {\sqrt {\alpha +\lambda {L \over D}+\sum \zeta }}}}$

kde ${\displaystyle \alpha }$ [-] je Coriolisovo číslo, ${\displaystyle \lambda }$ [-] součinitel ztráty třením, ${\displaystyle L}$ [m] délka spojovacího potrubí, ${\displaystyle D}$ [m] jeho průměr a ${\displaystyle \zeta }$ [-] součinitel místní ztráty.

Za dobu ${\displaystyle dt}$ se z nádrže A vyprázdní a v nádrži B naplní objem kapaliny ${\displaystyle dV=S_{A}dh_{A}=S_{B}dh_{B}}$ a rozdíl hladin se zmenší o ${\displaystyle dh=dh_{A}+dh_{B}}$. Lze tedy psát

${\displaystyle dV=\mu S{\sqrt {2gh}}dt=-S_{A}dh_{A}}$.

z čehož

${\displaystyle dt=-{S_{A} \over {\mu S{\sqrt {2g}}}}h^{-1/2}dh_{A}}$.

Pro integraci je nutné vyjádřit ${\displaystyle dh_{A}}$ pomocí ${\displaystyle dh}$ - protože ${\displaystyle dh_{B}={S_{A} \over S_{B}}dh_{A}}$, bude ${\displaystyle dh=dh_{A}{\Bigl (}1+{S_{A} \over S_{B}}{\Bigr )}}$a tedy

${\displaystyle dh_{A}={S_{B} \over {S_{A}+S_{B}}}dh}$

čili lze psát

${\displaystyle dt=-{S_{A}S_{B} \over {\mu S(S_{A}+S_{B}){\sqrt {2g}}}}h^{-1/2}dh}$.

Pro úplné vyrovnání hladin integrujeme od ${\displaystyle 0}$ do ${\displaystyle T}$, resp. od ${\displaystyle 0}$ do ${\displaystyle H}$, takže

${\displaystyle T={S_{A}S_{B} \over {\mu S(S_{A}+S_{B}){\sqrt {2g}}}}\int _{0}^{H}h^{-1/2}dh={2S_{A}S_{B} \over {\mu S(S_{A}+S_{B}){\sqrt {2g}}}}{\sqrt {H}}}$.

Pokud bychom chtěli dosáhnout jen určitého rozdílu hladin ${\displaystyle H_{*}}$ [m], postačí upravit integrační meze; výsledek je v tomto případě

${\displaystyle T={2S_{A}S_{B} \over {\mu S(S_{A}+S_{B}){\sqrt {2g}}}}{\bigl (}{\sqrt {H}}-{\sqrt {H_{*}}}{\bigr )}}$.

Případ výtoku pod pohyblivou hladinu je typický např. pro plnění a prázdnění plavebních komor; při plnění lze většinou uvažovat přítok z velké nádrže (s konstantní hladinou), při prázdnění naopak výtok do nádrže s konstantní hladinou - to je de facto totožné s výtokem do volna z nádrže bez přítoku (viz výše).

Řešení v tomto případě vychází ze základní diferenciální rovnice (viz výše), převedené do diferenčního schématu. Časový krok musí být přiměřeně malý, aby bylo dosaženo potřebné přesnosti řešení při rozumné výpočetní době. Při řešení se často využívá tzv. čáry zatopených ploch a čáry zatopených objemů, které jsou např. standardně zpracovány pro přehradní nádrže jako funkce kóty hladiny.

Typickým problémem, který se řeší tímto způsobem, je např. transformace povodňové vlny v přehradní nádrži. V tomto případě se ale obvykle uvažuje, spíše než výtok otvorem, přepad přes bezpečnostní přeliv, případně v součinnosti se základovými výpustmi.

• Výtok otvorem - sylabus přednášky HYA (FSv ČVUT) Archivováno 14. 9. 2016 na Wayback Machine.