Polární soustava souřadnic je taková soustava souřadnic v rovině , u které jedna souřadnice (označovaná r {\displaystyle r} vzdálenost bodu od počátku souřadnic , druhá souřadnice (označovaná φ {\displaystyle \varphi } úhel spojnice tohoto bodu a počátku od zvolené osy ležící v rovině (nejčastěji jí odpovídá osa x {\displaystyle x} kartézských souřadnic ).
Polární soustava souřadnic je vhodná v případech takových pohybů , při nichž se nemění vzdálenost tělesa od jednoho bodu (počátku souřadnic), například u pohybu po kružnici , případně se tato vzdálenost mění s nějakou jednoduchou závislostí.
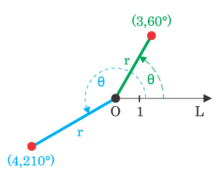
Souřadnicová síť v polárních souřadnicích Bod v polární soustavě souřadnic Ukázka dvou bodů v polárních souřadnicích: [r=3; φ=60°] a [r=4; φ=210°] Ukázka převodu polárních souřadnic [r; φ] na kartézské [x; y] Transformace Transformace polárních souřadnic na kartézské :
x = r cos φ {\displaystyle x=r\cos {\varphi }\,} y = r sin φ {\displaystyle y=r\sin {\varphi }\,} Převod kartézských souřadnic na polární :
r = x 2 + y 2 {\displaystyle r={\sqrt {x^{2}+y^{2}}}} φ = arctg ( y x ) {\displaystyle \varphi =\operatorname {arctg} \left({\frac {y}{x}}\right)} Tato převodní funkce však funguje jen na intervalu φ ∈ ⟨ 0 , π 2 ⟩ {\displaystyle \varphi \in \langle 0,{\frac {\pi }{2}}\rangle } funkce arctg(x ) . Abychom mohli popsat inverzi pro daný úhel na celém jeho definičním intervalu , bývá často používána funkce arctg2(y ,x ) definovaná jako
arctg2 ( y , x ) = { arctg ( y x ) , je-li ( x > 0 ) ∧ ( y > 0 ) , arctg ( y x ) + π , je-li ( x < 0 ) , arctg ( y x ) + 2 π , je-li ( x > 0 ) ∧ ( y < 0 ) , {\displaystyle \operatorname {arctg2} (y,x)=\left\{{\begin{matrix}\operatorname {arctg} \left({\frac {y}{x}}\right),\ \ \ \ \ \ &{\mbox{je-li }}(x>0)\wedge (y>0),\\\operatorname {arctg} \left({\frac {y}{x}}\right)+\pi ,\ &{\mbox{je-li }}(x<0),\ \ \ \ \ \ \ \ \ \ \ \ \ \\\operatorname {arctg} \left({\frac {y}{x}}\right)+2\pi ,&{\mbox{je-li }}(x>0)\wedge (y<0),\\\end{matrix}}\right.} Převod kartézských souřadnic na polární má potom zápis:
r = x 2 + y 2 {\displaystyle r={\sqrt {x^{2}+y^{2}}}} φ = arctg2 ( y , x ) {\displaystyle \varphi =\operatorname {arctg2} \left(y,x\right)} Vlastnosti Jedná se o ortogonální soustavu souřadnic s Lamého koeficienty
h r = 1 h φ = r {\displaystyle h_{r}=1\quad h_{\varphi }=r}
Délka infinitesimální úsečky se spočte jako
d s 2 = d r 2 + r 2 d φ 2 , {\displaystyle \mathrm {d} s^{2}=\mathrm {d} r^{2}+r^{2}\mathrm {d} \varphi ^{2},} tedy délka křivky obecně jako
∫ t 1 t 2 ( d r ( t ) d t ) 2 + r 2 ( d φ ( t ) d t ) 2 d t , {\displaystyle \int _{t_{1}}^{t_{2}}{\sqrt {\left({\frac {\mathrm {d} r(t)}{\mathrm {d} t}}\right)^{2}+r^{2}\left({\frac {\mathrm {d} \varphi (t)}{\mathrm {d} t}}\right)^{2}}}\mathrm {d} t,} kde t je parametr dané křivky a s je její délka od t 1 {\displaystyle t_{1}} t 2 {\displaystyle t_{2}}
Obsah infinitesimálního elementu plochy spočteme jako
d S = r d r d φ , {\displaystyle \mathrm {d} S=r\mathrm {d} r\mathrm {d} \varphi ,} takže celkový obsah spočteme integrací tohoto výrazu přes danou oblast vyjádřenou v polárních souřadnicích.
Christofelovy koeficienty Levi-Civitovy konexe generované Euklidovskou metrikou jsou dány vztahy
Γ r r r = Γ φ φ φ = Γ r r φ = Γ r φ r = Γ φ r r = 0 {\displaystyle {\Gamma ^{r}}_{rr}={\Gamma ^{\varphi }}_{\varphi \varphi }={\Gamma ^{r}}_{r\varphi }={\Gamma ^{r}}_{\varphi r}={\Gamma ^{\varphi }}_{rr}=0} Γ φ φ r = Γ φ r φ = 1 r {\displaystyle {\Gamma ^{\varphi }}_{\varphi r}={\Gamma ^{\varphi }}_{r\varphi }={\frac {1}{r}}} Γ r φ φ = − r {\displaystyle {\Gamma ^{r}}_{\varphi \varphi }=-r} Diferenciální operátory v polárních souřadnicích ∇ f = ∂ f ∂ r r ^ + 1 r ∂ f ∂ φ φ ^ {\displaystyle \nabla f={\partial f \over \partial r}{\boldsymbol {\hat {r}}}+{1 \over r}{\partial f \over \partial \varphi }{\boldsymbol {\hat {\varphi }}}}
∇ ⋅ A = 1 r ∂ ( r A r ) ∂ r + 1 r ∂ A φ ∂ φ {\displaystyle \nabla \cdot \mathbf {A} ={1 \over r}{\partial \left(rA_{r}\right) \over \partial r}+{1 \over r}{\partial A_{\varphi } \over \partial \varphi }}
Δ f = ∇ 2 f = 1 r ∂ ∂ r ( r ∂ f ∂ r ) + 1 r 2 ∂ 2 f ∂ φ 2 {\displaystyle \Delta f=\nabla ^{2}f={1 \over r}{\partial \over \partial r}\left(r{\partial f \over \partial r}\right)+{1 \over r^{2}}{\partial ^{2}f \over \partial \varphi ^{2}}}
Δ A = ( Δ A r − A r r 2 − 2 r 2 ∂ A φ ∂ φ ) r ^ + ( Δ A φ − A φ r 2 + 2 r 2 ∂ A r ∂ φ ) φ ^ {\displaystyle \Delta \mathbf {A} =\left(\Delta A_{r}-{A_{r} \over r^{2}}-{2 \over r^{2}}{\partial A_{\varphi } \over \partial \varphi }\right){\boldsymbol {\hat {r}}}+\left(\Delta A_{\varphi }-{A_{\varphi } \over r^{2}}+{2 \over r^{2}}{\partial A_{r} \over \partial \varphi }\right){\boldsymbol {\hat {\varphi }}}}
Externí odkazy 

 Obrázky, zvuky či videa k tématu polární soustava souřadnic na Wikimedia Commons
Obrázky, zvuky či videa k tématu polární soustava souřadnic na Wikimedia Commons 




