Průjezd obloukem

Průjezd obloukem je v dopravě stav, kdy vozidlo mění směr pohybu (zatáčí). Aby mohlo vozidlo zatočit, je nutno zajistit dostatečnou dostředivou sílu. V případě silniční dopravy to znamená dostatečné tření resp. adhezi mezi koly vozidla a povrchem vozovky, v případě kolejové dopravy zajišťuje vedení kola (resp. dvojkolí) na něm vytvořený okolek. Mezi další opatření, která mají zajistit hladký průjezd obloukem, patří na straně vozidla vhodný návrh konstrukce pojezdu a na straně jízdní dráhy vhodné převýšení (náklon) a přechodnice (traťový úsek, v němž se křivost plynule mění z přímky na kruhový oblouk).

Schopnost vozidla projíždět oblouky o určitém minimálním poloměru je zadaný parametr pro jeho konstrukci. Sjednává se mezi výrobcem a zákazníkem, v České republice je podle Dopravního řádu drah povinně uváděna v technických podmínkách vozidla, a to jednak pro jízdu traťovou rychlostí, jednak pro jízdu za případných omezujících podmínek.^[1]

Geometrické poměry

Prvním předpokladem úspěšného průjezdu kolejového vozidla obloukem je, že konstrukce koleje a vozidla je vzájemně kompatibilní. Zpravidla jsou to vlastnosti vozidla, které se musejí přizpůsobit parametrům sítě. Při konstrukci vozidla je třeba zaručit nejen, že se vozidlo do oblouku „vejde“, ale i správnou vzájemnou interakci vozidel (rozměry nárazníků, které se nesmějí zaklesnout, přiměřené délky hadic, kabelů, …) i částí vozidla (dostatečná pohyblivost podvozků).

Průjezdný průřez

Průjezdný průřez je jedním ze základních parametrů tratě. V oblouku zaujímá skříň vozidla tětivovou polohu. Tento fakt musí být zohledněn již při konstrukci vozidla. Pouze v oblouku o poloměru menším než 250 m se průjezdný profil rozšiřuje.^[2] U delších vozidel se proto navrhuje vozová skříň užší.

Postup stanovení maximálních rozměrů vozidla je poměrně komplikovaný a zahrnuje množství vstupních parametrů. Pro vozidla provozovaná na sítích členských zemí UIC a tedy i v ČR je popsán ve vyhlášce UIC 505-1.

Pojezd a kolej

Dvounápravové pojezdy a podvozky nepředstavují problém z hlediska pozice pojezdu v koleji v oblouku. Jiná situace nastává u vozidel, které mají tři a více náprav vedených pevně v rámu. S touto problematikou se potýkali zejména konstruktéři parních lokomotiv. Vznikla tak řada více či méně použitelných řešení, z nichž se nejvíce prosadily nejjednodušší konstrukce s několika spřaženými dvojkolími v jednom rámu, kde byl průjezd obloukem umožněn konstrukcí Karla Gölsdorfa spočívající v kombinaci pevných a příčně posuvných dvojkolí a zeslabených okolků na některých kolech uvnitř pevného rozvoru. Méně používanou cestou bylo použití děleného pojezdu se samostatnými parními stroji v lokomotivách typu mallett, garratt a dalších.

• 

  Gölsdorfovy nápravy

• 

  Malletova konstrukce

Vogelova metoda

Pro zjednodušení vyšetření postavení pojezdu v oblouku vyvinul Vogel geometrickou metodu, která umožní vyšetření polohy jednotlivých dvojkolí pojezdu. Základním prvkem této jednoduché metody je zpodobnění jednotlivých dvojkolí jako bodů a koleje v podobě šířky kolejového kanálu. Obě osy používají různá měřítka, takže kruhový oblouk je zpodobněn jako elipsa. Tato komplikace je vyvážena zřetelným zobrazením poloh jednotlivých dvojkolí.

• 

  Vogelova metoda uplatněná na lokomotivu ř. E 465.0 …

• 

  … a obrázek, jak vypadá postavení pojezdu v oblouku ve skutečnosti

Vozidlo v oblouku – příčné zrychlení

Při průjezdu kolejového vozidla kruhovým obloukem je vozidlo vedeno do oblouku dráhou. Setrvačnost vozidla se vůči dráze projevuje jako odstředivá síla. Velikost této síly je dána součinem hmotnosti vozidla a příčného (dostředivého) zrychlení, které se vypočte jako podíl druhé mocniny rychlosti vozidla poloměru oblouku: a=v²/R [m/s²].

Přípustná velikost příčného zrychlení je dána řadou parametrů koleje i vozidla. Při průjezdu obloukem nejen že nesmí dojít k takovému nárůstu odstředivé síly, který by vedl k poškození koleje nebo vozidla, případně k jeho převržení, ale je třeba dbát i na přepravovaný náklad a pohodlí cestujících. V minulosti proto různé železniční správy omezily přípustnou hodnotu příčného zrychlení (resp. jeho nevyrovnané složky – viz dále). U ČSD byla tato hodnota stanovena na 0,65 m/s².

Převýšení vnějšího kolejnicového pásu

Aby bylo možno projíždět oblouky vyšší rychlostí, než dovolovala stanovená hodnota příčného zrychlení, začaly se při stavbě železnic uplatňovat převýšené oblouky, neboli oblouky s vnějším kolejnicovým pásem ve vyšší poloze, než je poloha vnitřního kolejnicového pásu. Vlivem náklonu koleje se výsledná síla, kterou vozidlo působí na kolej, a která je vektorovým součtem tíhové a odstředivé síly, rozloží na dvě složky: kolmou k rovině koleje a rovnoběžnou s rovinou koleje. V ideálním případě je rovnoběžná složka rovna nule. Tento stav lze vyjádřit vzorcem

${\displaystyle h={\frac {s.v^{2}}{R.g}}}$,

kde h je převýšení, s vzdálenost styčných kružnic, poloměr oblouku R, rychlost v a tíhové zrychlení g . Jinými slovy poměr převýšení a vzdálenosti styčných kružnic je roven poměru dostředivého a tíhového zrychlení.

Při návrhu převýšení nelze spoléhat na to, že všechna vozidla budou projíždět daným obloukem navrhovanou rychlostí. Proto se vychází z předpokládané skladby vozidel a jejich rychlostí, kterými bude příslušný oblouk pojížděn a navržené převýšení je určitým kompromisem. Je-li přitom navrženo příliš nízké převýšení, omezuje se maximální rychlost vlaků, naopak vysoká hodnota převýšení způsobuje u pomalu jedoucích těžkých nákladních vlaků zvýšené namáhání vnitřního kolejnicového pásu. Maximální hodnota převýšení bývá u klasické trati omezena na 150 mm (platilo na většině evropských drah, například Francouzské dráhy ale měly na některých tratích povoleno převýšení až 192 mm).^[3]

Přechodnice a vzestupnice

Přechodnice je část tratě, ve kterém trať přechází z přímého směru do oblouku konstantního poloměru, případně přechází z oblouku daného poloměru do oblouku jiného poloměru. Účelem přechodnice je odstranit náraz dostředivé síly vznikající při přechodu tělesa z přímočarého pohybu na kruhový pohyb (průjezdu obloukem), resp. zajistit pozvolný nárůst této síly. Moderní přechodnice nepoužívají ani lineární nárůst křivosti, ale jejich průběh je dále upraven s ohledem na konstrukci vozidel a požadavek na plynulou a měkkou změnu mezi ustálenou polohou vozidla v přímé a v kruhovém oblouku.

Přechodnice je zpravidla kombinována se vzestupnicí, to znamená, že v přechodnici se zároveň plynule zvedá vnější kolejnicový pás na hodnotu odpovídající převýšení navazujícího kruhového oblouku.^[4]

Vozidla s naklápěcími skříněmi

(c) ​Japanese Wikipedia user 出々 吾壱, CC BY-SA 3.0

Snaha o zvyšování rychlosti na stávajících tratích vedla ke konstrukci několika typů vozidel s naklápěcí vozovou skříní, z nichž nejznámější je pravděpodobně Pendolino. Tato vozidla kompenzují účinek odstředivého zrychlení na cestující, nikoli však účinek vozidla na trať. Jestliže se uvádí možnost zvýšení rychlosti v oblouku až o 30%, znamená to, že dostředivé zrychlení, které je úměrné druhé mocnině rychlosti, se zvýší 1,3²×, čili 1,69×.

Příklad

Klasická souprava v oblouku o poloměru 300 m s převýšením 122 mm. Dovolená hodnota nevyrovnaného příčného zrychlení 0,65 m/s²:

Přípustné příčné zrychlení jako součet složky vyrovnané převýšením oblouku a nevyrovnané složky:

${\displaystyle a={\frac {g.h}{s}}+0,65={\frac {9,81.122}{1500}}+0,65=0,8+0,65=1,45[m/s^{2}]}$

Dovolená rychlost pro klasické vozidlo:

${\displaystyle v={\sqrt {a.R}}={\sqrt {1,45.300}}=20,9[m/s]=75[km/h]}$

Pendolino v tomtéž oblouku při rychlosti o 30 % vyšší:

${\displaystyle v=1,3.20,9=27,2[m/s]}$

${\displaystyle a={\frac {v^{2}}{R}}={\frac {27,2^{2}}{300}}=2,46[m/s^{2}]}$

Vyrovnaná složka daná převýšením oblouku zůstává stejná, jako na začátku: 0,8 m/s², hodnota nevyrovnaného příčného zrychlení tedy činí 2,46 – 0,8 = 1,66 m/s². Jinými slovy Pendolino sice umožní zvýšení rychlosti v daném oblouku o 30% při zachování komfortu cestujících, avšak ve vztahu vozidla a koleje vede toto zvýšení rychlosti k nárůstu silového účinku vozidla na kolej v příčném směru na více než 2,5násobek.

Vyšetření polohy pojezdu na základě minima řídících sil

Historický vývoj teorie průjezdu obloukem

Až do roku 1883 se všeobecně věřilo, že vozidlo, které projíždí obloukem rychlostí vyšší, než odpovídá převýšení oblouku, tj. s nenulovým nevyrovnaným příčným zrychlením, doléhá okolky obou vodících dvojkolí na vnější kolejnici. Až v roce 1883 provedl Mackenzie pokusy, které tento názor zpochybňovaly. Definitivně jej vyvrátily studie Roye publikované v roce 1884 a Wellingtonovy pokusy provedené v roce následujícím.

Roy-Wellingtonova teorie říkala, že zadní vodící dvojkolí má snahu zaujímat radiální postavení. Ač tato teorie vycházela z ne zcela přesných předpokladů, byla dlouho uznávaná. S dalším podnětem přišel Richard Helmoltz v roce 1888, který navrhl určovat polohu vozidla z podmínek statické rovnováhy. Této myšlenky se ujal ruský inženýr Choloděckij, který v letech 1896–1898 první přišel s názorem o minimu řídící síly. Další rus, Ceglinskij, publikoval řešení silového působení při průjezdu obloukem v roce 1903.

Ve stejném roce přišel Němec Uebelacker s myšlenkou středu tření, pravděpodobně nezávisle na ruských výzkumech. Jeho pokračovatel Heumann uveřejnil o deset let později grafickou metodu ke stanovení polohy vozidla na základě minima řídící síly – tzv. Heumannova metoda. Na něj navázali Bäseler, Troitsch, Hiller a další, kteří vyvinuli jiné grafické nebo početní metody, avšak se stejnými výsledky, jako metoda Heumannova.

Přednostmi Heumannovy metody jsou přímé řešení bez zkoušení, přehlednost vlivu jednotlivých sil na polohu vozidla a velikost řídící síly, posouzení jízdních odporů a opotřebení okolků. Nedostatkem jsou pak její zjednodušující předpoklady – válcová jízdní plocha kol, stejné zatížení, absence hnacích nebo brzdících sil. To vede k tomu, že z absolutního hlediska jsou získané výsledky jen přibližné, výborně však poslouží k porovnání jednotlivých pojezdů.

Další zdokonalení této metody přinesl Borgeaud v letech 1937 a 1944 – dokázal pracovat s rozdílnými kolovými tlaky i s hnacími a brzdícími silami. Nezávisle na německé škole pokračoval vývoj teorie průjezdu obloukem v Sovětském svazu. Zde publikovali své studie Koroljev (1940, 1950, 1952), Lvov a Voroběv (1937), Mistěnko (1950), Dorfman (1954), Kucenko (1954) a další.^[5]

Heumannova metoda

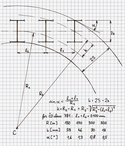
Heumannova metoda spočívá v grafickém vyšetření minima řídících sil a nalezení takzvaného středu tření. Pokud se rotační pohyb podvozku, který má střed otáčení ve středu oblouku, rozloží na dva pohyby – posuvný pohyb po kružnicích o poloměru shodném s poloměrem oblouku a rotaci kolem svislé osy, pak ve svislém průmětu tato osa tvoří střed tření. Také lze říci, že kolmice k ose vozidla procházející středem tření prochází zároveň středem oblouku.

U dvou- a třínápravových podvozků se střed tření nachází v podélné ose podvozku (event. rámového pojezdu), a to přibližně v místě poslední pevně vedené nápravy ve směru jízdy.

Střed tření a postavení podvozku (pojezdu) v oblouku

• 

  Schema třínápravového podvozku v oblouku – volná poloha

• 

  Dvounápravový podvozek ve vzpříčené poloze (zadní dvojkolí nabíhá na vnitřní kolejnici)

Jestliže je známá poloha středu tření, lze si zpětně udělat obraz o postavení podvozku (pojezdu) v koleji. Na levém obrázku je schema třínápravového podvozku v oblouku. Při jistém zjednodušení postačí k výpočtu potřebné šířky kolejového kanálu pro volný průjezd obloukem (bez řídící síly na posledním dvojkolí) Pythagorova věta. Šířka kolejového kanálu k musí být větší, než

${\displaystyle R-{\sqrt {R^{2}-d^{2}}}}$ ,

kde d je celkový rozvor podvozku a R poloměr projížděného oblouku.

Tento vzorec se dá vzhledem k malým úhlům zjednodušit na tvar

${\displaystyle k\geq {\frac {d^{2}}{2R}}}$

Vyznačený úhel α je úhel náběhu, tj. úhel roviny předního kola a tečny k oblouku kolejnice v místě styku,^[6][7] zároveň (podle geometrické podobnosti trojúhelníků) úhel vychýlení osy přední nápravy od směru ke středu oblouku. Pokud je šířka kolejového kanálu menší, dojde k dolehnutí zadního dvojkolí ve směru jízdy na vnitřní kolejnici – tato poloha se nazývá vzpříčená a je zobrazena na obrázku vpravo.

Dvojkolí v oblouku

Při průjezdu pojezdu kolejového vozidla obloukem dochází ke skluzům mezi jízdní plochou kola a kolejnicí. Tyto skluzy se dělí na tři základní typy:

• podélné skluzy – vznikají na základě rozdílu obvodové rychlosti kola v místě styčné kružnice a dopředné rychlosti vozidla
• příčné skluzy – vznikají tím, že dvojkolí nezaujme radiální polohu, dvojkolí doléhá okolkem na hlavu kolejnice a během jízdy je průběžně posouváno v příčném směru
• spin – je způsoben tím, že styk kola s kolejnicí se neodehrává v bodě, ale v ploše, kolo se vůči kolejnici natáčí kolem svislé osy.

Vliv tvaru jízdních ploch kol

Tvar jízdní plochy kola železničního dvojkolí není zpravidla válcový, jak zjednodušeně předpokládá Heumannova metoda, ale je řešen tak, že na vnější straně kola má menší průměr a na vnitřní straně u okolku má větší průměr. Původně se používal kuželový profil kola, ve 2. polovině 20. století se přešlo na tzv. opotřebené profily, které zajišťují nižší kontaktní namáhání ve styku kolo – kolejnice. V ideálním případě – pokud to konstrukce vozidla umožní – při vjezdu do oblouku dvojkolí samo zaujme pozici blíže k vnější kolejnici oblouku a tím dojde ke změně geometrie odvalování na vnitřním i vnějším kole dvojkolí. Pokud má dvojkolí pevnou nápravu a obě kola mají stejné otáčky, tak se vnitřní kolo odvaluje po menším průměru a má menší obvodovou rychlost, vnější kolo se odvaluje po větším průměru a má větší obvodovou rychlost. Změna průměrů styčných kružnic je znázorněna na obrázku. Posunutím dvojkolí z osy koleje k vnější kolejnici se docílí efektu, kdy styčné kružnice obou kol definují kužel s vrcholem ve středu oblouku a dvojkolí projíždí obloukem bez podélných skluzů. V průběhu životnosti dvojkolí se tvar jízdní plochy, a tím i ekvivalentní konicita opotřebením mění, což má vliv i na průjezd obloukem. Pokud dvojkolí nejsou spojena pevnou nápravou (Talgo), nemá konicita kol na průjezd obloukem vliv.

Vliv vedení dvojkolí

Při průjezdu vozidla obloukem má zásadní vliv na velikost skluzů, řídící síly a následně i opotřebení konstrukce pojezdu vozidla, zejména vedení dvojkolí. Z hlediska dokonalého průjezdu obloukem je žádoucí, aby vedení dvojkolí umožnilo zaujmout nápravě radiální polohu, případně ji dokonce do této polohy postavilo. Tento požadavek je poněkud v rozporu s požadavkem na co nejvyšší tuhost vedení dvojkolí pro zaručení stability chodu při vyšších rychlostech.

• 

  Tuhé vedení (tuhost v příčném směru není na obrázcích znázorněna)

• 

  Pružné vedení umožňující radiální postavení dvojkolí v oblouku

Na obrázku vlevo je znázorněn podvozek s tuhým vedením dvojkolí. Přední dvojkolí ve směru jízdy (na obrázku vpravo) nabíhá na vnější kolejnici. Za příznivých podmínek může nastat situace, že poměr poloměrů styčných kružnic obou kol odpovídá poloměru oblouku, dvojkolí projíždí obloukem bez podélných skluzů, nikoli však bez příčných. Zadní dvojkolí ve směru jízdy (na obrázku vlevo) naopak zaujímá téměř ideální radiální polohu, projíždí tedy obloukem téměř bez příčných skluzů. Avšak je rámem vedeno blíže k vnitřní kolejnici, neuplatní se proto efekt kuželovitosti dvojkolí, rozdíl dráhy vnitřního a vnějšího kola se vyrovnává podélnými skluzy. Na pravém obrázku je podvozek s radiálně stavitelnými dvojkolími. V ideálním případě zaujmou obě dvojkolí radiální polohu, čímž odpadnou příčné skluzy, a dojde k jejich příčnému posunutí odpovídajícímu poloměru oblouku, čímž odpadnou skluzy podélné. Spin zůstává v obou případech stejný. Uvádí se, že tímto způsobem lze snížit opotřebení kol i kolejnic proti tuhému vedení až na desetinu.^[8] V praxi se konstrukce podvozků pohybují víceméně mezi oběma uvedenými extrémy podle toho, které hledisko je považováno za důležitější, a to včetně hledisek ekonomických.

Mezipodvozková vazba a kloubové spojení podvozků

Pro snížení úhlu náběhu a řídící síly, zejména na 1. dvojkolí ve směru jízdy, se u podvozkových vozidel někdy používá mezipodvozková vazba nebo kloubové spojení. Druhý podvozek přitom působí v příčném směru na zadní část rámu předního podvozku a natáčí jej směrem k tětivové poloze. Zároveň dochází k přenesení části řídící síly z prvního dvojkolí druhého podvozku do mezipodvozkové vazby nebo kloubu.

Kloubové spojení podvozků se používalo u parních lokomotiv Malletovy konstrukce. V elektrické trakci je použito například u odklizových lokomotiv – jedná se o lokomotivy pro malé rychlosti s vysokou tažnou silou, které jezdí často v obloucích malých poloměrů po tratích s nekvalitním svrškem.

V případě klasických lokomotiv se upřednostňuje použití mezipodvozkové vazby. Ta se od kloubového spojení liší tím, že umožňuje omezený vzájemný pohyb podvozků, aniž by tyto na sebe vzájemně silově působily. Teprve při větším vzájemném pohybu (jednotky až desítky mm dle typu) dojde k vymezení vůle a podvozky se o sebe opřou prostřednictvím pružné vazby. Použití mezipodvozkové vazby je z hlediska zmírnění úhlu náběhu a snížení řídících sil méně účinné, než kloubové spojení, avšak na druhou stranu nemá negativní vliv na stabilitu chodu v přímé koleji při vyšších rychlostech.^[9]

Bezpečnost proti vykolejení

Vozidlo v oblouku je nuceno měnit vlivem působení jízdní dráhy směr. Ve srovnání s jízdou v přímé koleji zde dochází ke zvýšenému působení sil ve vodorovné rovině ve směru kolmém na směr jízdy. Tyto síly se přenášejí kontaktem hlavy kolejnice s okolkem. Kontaktní bod okolku s kolejnicí předbíhá průsečík průmětu osy nápravy do roviny koleje a boku hlavy kolejnice, takže díky tření mezi okolkem a kolejnicí má okolek snahu kolo zvedat a vyšplhat se na hlavu kolejnice. Situace se zhoršuje se zvětšujícím se úhlem náběhu, s počtem náprav v podvozku (nejsou-li radiálně stavitelné) i s rostoucím koeficientem tření. V praxi je zaveden limit pro poměr vodící a svislé kolové síly Y/Q. Tento poměr je stanoven pro všechna vozidla jako limitní pro bezpečný průjezd obloukem.

Nejnebezpečnější situace nastává při výjezdu z převýšeného oblouku, kdy je vedoucí kolo odlehčeno – vnější kolejnicový pás pod ním klesá, zatímco řídící síla se nemění. Naopak pozitivní vliv má snížení koeficientu tření mezi okolkem a kolejnicí, stejně tak i mezi jízdními plochami kol a kolejnicemi, což bývá zejména u hnacích vozidel na závadu. Dále má pozitivní vliv rychlost – vodící kolo je přitlačováno ke kolejnici reakcí na dostředivou sílu. Při velkém překročení návrhové rychlosti v oblouku zpravidla nedojde k vykolejení, ale k převržení vozidla, případně k vybočení koleje. K vykolejení může dojít, pokud není hrana hlavy kolejnice hladká – například při vybočeném nebo povoleném styku.

Odkazy

Reference

Literatura

• Bek, J. a kol.: Elektrické lokomotivy, NADAS, Praha 1976, 21-010-76 05-94
• Podrobné vysvětlení problematiky na stránkách VUT Brno - souhrn přednášek doc. Pláška o železnici se zaměřením na kolej a její vzájemné působení s vozidlem
• Universita Pardubice, Základy dopravní techniky – železniční doprava, Ing. Michael Lata, PhD.
• Zelenka, J., Kohout, M.: Možnosti ovlivnění jízdních a vodících vlastností kolejových vozidel parametry dopravní cesty, Nová železniční technika 3/2010, KPM CONSULT, a.s., Brno, ISSN 1210-3942

Související články

• Pojezd parní lokomotivy
• Uspořádání pojezdu
• Železniční dvojkolí
• Ekvivalentní konicita
• Vogelova metoda
• Heumannova metoda
• Vykolejení