Pravidelná síť

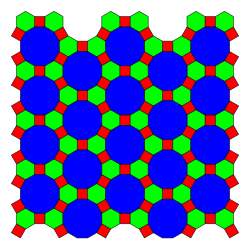
V geometrii je pravidelná síť (také pravidelná teselace či pravidelné vyplnění roviny) souvislé uspořádání pravidelných konvexních mnohoúhelníků v rovině, přičemž délky stran všech mnohoúhelníků jsou stejně velké a pořadí daných mnohoúhelníků je u všech vrcholů shodné. Například síť 3.6.3.6 je tvořena trojúhelníky a šestiúhelníky se stejnou délku strany, které jsou při vrcholu vždy střídavě dva a dva.

Existují právě tři pravidelné a osm polopravidelných sítí^[1][2]. Mnohoúhelníky, které tvoří tyto sítě, jsou čtverec, rovnostranný trojúhelník a pravidelný šestiúhelník, osmiúhelník a dvanáctiúhelník.

Seznam pravidelných sítí

Platónské a Archimedovské sítě	obrázek
Čtvercová (pravoúhlá) síť 4.4.4.4 pravidelná síť
Zkrácená čtvercová síť 4.8.8 polopravidelná síť
Zkosená čtvercová síť 3.3.4.3.4 polopravidelná síť
Šestiúhelníková (hexagonální) síť 6.6.6 pravidelná síť
Trihexagonální síť 3.6.3.6 polopravidelná síť
Zkrácená hexagonální síť 3.12.12 polopravidelná síť
Trojúhelníková síť 3.3.3.3.3.3 pravidelná síť
Rhombitrihexagonální síť 3.4.6.4 polopravidelná síť
Zkrácená trihexagonální síť 4.6.12 polopravidelná síť
Zkosená trihexagonální síť 3.3.3.3.6 polopravidelná síť
Prodloužená trojúhelníková síť 3.3.3.4.4 polopravidelná síť

Zajímavosti

Kartézský systém souřadnic

Včelí plástev

Rhombitrihexagonální podlaha kostela ve španělské Seville

Hexagonální odlučnost čediče

Nejsnadněji sestrojitelná je pravoúhlá síť. Využívá se ve stavebnictví, jako podklad pro sešity, v matematice jako podklad pro kartézskou soustavu souřadnic. Hexagonální strukturu mají včelí plástve, a to díky fyzikálním vlastnostem vosku^[3]. Hexagonální odlučnost má také vyvřelá hornina čedič.

Reference

V tomto článku byl použit překlad textu z článku List of convex uniform tilings na anglické Wikipedii.