Reuleauxův trojúhelník

Reuleauxův trojúhelník je rovinný útvar, který vznikne protnutím tří kružnic, jež mají každá střed v místě, kde se zbylé dvě dotýkají. Jeho okraj tvoří křivka s konstantní šířkou, nejjednodušší a nejznámější taková křivka po kružnici samotné. Každý bod jedné strany má konstantní vzdálenost od protějšího vrcholu. Jeho prostorovou obdobou je Reuleauxův tetraedr.

Reuleauxův trojúhelník nese jméno po Franzi Reuleauxovi, německém inženýrovi z 19. století.[1][2] Tyto tvary však byly známy již dávno před ním, byly například využity gotickými architekty při navrhování kostelních oken či Leonardem da Vincim pro mapová zobrazení.
Vlastnosti

Nejzásadnější matematickou vlastností Reuleauxova trojúhelníku je jeho konstantní šířka. To znamená, že všechny body každé ze stran mají stejnou vzdálenost od protějšího vrcholu.
Prvním matematikem, který popsal křivky konstantní šířky a určil, že Reuleauxův trojúhelník je jednou z nich, mohl být Leonhard Euler ve své práci De curvis triangularibus, kterou napsal roku 1771 a publikoval roku 1781.[3][4]
Dle Blaschkeovy–Lebesgueovy věty má Reuleauxův trojúhelník ze všech křivek konstantní šířky nejmenší možný obsah, který je roven
kde je konstantní šířka.[2] Pro porovnání, křivka konstantní šířky s největším obsahem je kruh, jehož obsah je
- .[5]
Reuleauxův trojúhelník má u svých vrcholů nejmenší možný úhel pro křivky konstantní šířky, a to 120°.
Ze všech křivek konstantní šířky lze Reuleauxovu trojúhelníku vepsat největší i nejmenší rovnostranný trojúhelník. Největší je ten, jehož vrcholy jsou totožné s vrcholy samotného Reuleauxova trojúhelníku. Nejmenší je ten, který spojuje středy jeho stran.
Rotace uvnitř čtverce

Jakákoliv křivka konstantní šířky může tvořit rotor uvnitř čtverce. To znamená, že může provést úplnou rotaci ve čtverci, po celou dobu rotace je celým svým obsahem uvnitř čtverce a neustále se dotýká všech čtyř stran čtverce. Reuleauxův trojúhelník je rotorem s nejmenším možným obsahem. V průběhu rotace nezůstává osa v jediném bodě, ale opisuje křivku tvořenou částmi oblouků čtyř elips.[6] Kvůli tomu, že úhel u vrcholů Reuleauxova trojúhelníku je 120°, nemůže při rotaci dosáhnout některých bodů u vrcholu čtverce (kde je úhel pouze 90°). Během rotace tak vytvoří obrazec s mírně zaoblenými rohy, které jsou také částmi oblouků elips.
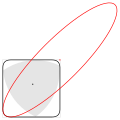
- Reuleauxův trojúhelník rotující ve čtverci a elipsa, jejíž část během rotace opisuje střed trojúhelníku
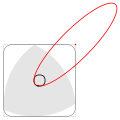
- Elipsa ohraničující levý dolní roh oblasti obsažené Reuleauxovým trojúhelníkem během rotace
V jakémkoliv okamžiku rotace se dva vrcholy Reuleauxova trojúhelníku dotýkají dvou sousedních stran čtverce a třetí vrchol se pohybuje po křivce u protějšího vrcholu čtverce. Během rotace obsáhne Reuleauxův trojúhelník přibližně 98,77% plochy čtverce.[2]
Konstrukce

Reuleauxův trojúhelník může být sestrojen přímo třemi kružnicemi, nebo pomocí rovnostranného trojúhelníku.
Na konstrukci pomocí tří kružnic stačí pouze kružítko a postup je velmi jednoduchý. Nejprve zvolíme libovolné dva body v rovině. Pomocí kružítka narýsujeme kružnici se středem v jednom z bodů, která druhým námi zvoleným bodem prochází. Poté narýsujeme druhou kružnici o stejném poloměru se středem v druhém bodě (která tedy prochází prvním bodem). Nakonec narýsujeme třetí kružnici se stejným poloměrem, která má střed v jednom z průsečíků prvních dvou kružnic (a prochází tak oběma zvolenými body). Průnik tří kruhů ohraničených takovýmito kružnicemi je Reuleauxův trojúhelník.
Můžeme také postupovat tak, že nejprve narýsujeme rovnostranný trojúhelník. Poté narýsujeme část kružnice se středem v jednom vrcholu, která spojuje zbývající dva vrcholy. Když to provedeme se všemi vrcholy, dostaneme Reuleauxův trojúhelník.
Použití
Strojírenství
Reuleauxův trojúhelník je součástí mechanismů sloužících k převodu otáčivého pohybu na posuvný. Právě tyto mechanismy studoval Franz Reuleaux.[7] Jsou známy ale i starší případy využití Reuleauxova trojúhelníku ve strojírenství, například některé parní stroje z doby kolem roku 1830 mají vačky tohoto tvaru.[8]
Pro svou schopnost rotace ve čtverci se Reuleauxův trojúhelník využívá u vrtáků pro vrtání téměř dokonale čtvercových děr.[2][9] Další Reuleauxovy mnohoúhelníky se používají pro vrtání děr ve tvaru pětiúhelníku, šestiúhelníku či osmiúhelníku.[9]
Píst Wankelova motoru má tvar zaobleného trojúhelníku, a tak se často uvádí jako příklad využití Reuleauxova trojúhelníku.[1] Jedná se ale o omyl, neboť píst má tvar jinak zaobleného trojúhelníku.[10]
Architektura

V gotické architektuře byl Reuleauxův trojúhelník používán jako tvar oken nebo prvek kružby či jiných architektonických dekorací.[1] Můžeme jej nalézt například v Katedrále Narození Panny Marie v Miláně.
Reuleauxův trojúhelník byl a je využíván i jinými architektonickými slohy. Například Leonardo da Vinci jej použil jako návrh tvaru opevnění. Z moderních staveb, které nějakým způsobem využívají tento tvar, můžeme zmínit Donauturm, Torre de Collserola, Mercedes–Benz Museum či KölnTriangle. V mnoha případech užití v moderní architektuře se však jedná o jinak zaoblené trojúhelníky, které jsou odlišné od Reuleauxova trojúhelníku.
Mapová zobrazení
Jedním z raných použití Reuleauxova trojúhelníku je mapa světa, kterou vytvořil Leonardo da Vinci kolem roku 1514. Kulový povrch Země rozdělil na osm částí a každou z nich zobrazil na Reuleauxův trojúhelník.[11][12][13]

Podobné mapy založené na Reuleauxově trojúhelníku publikoval také Oronce Finé v roce 1551 nebo John Dee roku 1580.[13]
Ostatní použití
Reuleauxův trojúhelník je zajímavý a přitom jednoduchý tvar, a tak není divu, že jej různé společnosti využívají ve svých logách. Objevil se například v logu již zaniklé belgické ropné společnosti Petrofina[14] či automobilky Lancia. Systém Národních turistických stezek ve Spojených státech používá značky ve tvaru Reuleauxova trojúhelníku.[15]

Tvar Reuleauxova trojúhelníku je používaný pro výrobu trsátek či tužek, které jsou výrobci označovány za pohodlnější a ergonomičtější než běžné tužky tvaru kruhu nebo šestiúhelníku, a navíc mají menší tendenci skutálet se ze stolu (protože jejich těžiště musí při kutálení překonávat větší výškový rozdíl).

Reuleauxův trojúhelník je v některých částech světa používán jako tvar matice uzávěru hydrantů. Běžným klíčem se takové matice dají kvůli své konstantní šířce jen velmi těžko povolit a je třeba mít speciální klíč, kterým disponují hasiči. To umožňuje hasičům hydrant běžně užívat, ale zabraňuje ostatním nezákonným použitím.
Reference
- ↑ a b c ALSINA, Claudi; NELSEN, Roger B. Icons of Mathematics: An Exploration of Twenty Key Images. [s.l.]: Mathematical Association of America, 2011. (Dolciani Mathematical Expositions; sv. 45). ISBN 978-0-88385-352-8. S. p. 155..
- ↑ a b c d PICKOVER, Clifford A. Matematická kniha. [s.l.]: Dokořán, 2012. ISBN 978-80-7363-368-4. S. 266-267..
- ↑ REICH, Karin. Leonhard Euler: Life, Work and Legacy. Redakce Bradley Robert E.. [s.l.]: Elsevier, 2007. (Studies in the History and Philosophy of Mathematics; sv. 5). ISBN 9780444527288. doi:10.1016/S0928-2017(07)80026-0. Kapitola Euler's contribution to differential geometry and its reception, s. 479–502.. See in particular section 1.4, "Orbiforms, 1781", pp. 484–485.
- ↑ EULER, Leonhard. De curvis triangularibus. Acta Academiae Scientiarum Imperialis Petropolitanae. 1781, s. 3–30. Dostupné online. (latinsky).
- ↑ GRUBER, Peter M. Convexity and its Applications. [s.l.]: Birkhäuser, 1983. Dostupné online. ISBN 978-3-7643-1384-5. S. 67.
- ↑ GLEIFTNER, Winfried; ZEITLER, Herbert. The Reuleaux triangle and its center of mass. Results in Mathematics. May 2000, s. 335–344. doi:10.1007/bf03322004. S2CID 119600507..
- ↑ KLEE, Victor; WAGON, S. Old and New Unsolved Problems in Plane Geometry and Number Theory. [s.l.]: Cambridge University Press, 1991. (Dolciani mathematical expositions; sv. 11). Dostupné online. ISBN 978-0-88385-315-3. S. 21..
- ↑ PETERSON, Ivars. Rolling with Reuleaux. MathTrek. ScienceNews, October 19, 1996. Dostupné online.. Reprinted in PETERSON, Ivars. Mathematical Treks: From Surreal Numbers to Magic Circles. [s.l.]: Mathematical Association of America, 2002. (MAA spectrum). Dostupné online. ISBN 978-0-88385-537-9. S. 141–144..
- ↑ a b How to drill square hexagon octagon pentagon holes. Wilmerding, Pennsylvania: Watts Brothers Tool Works, 1950–1951.
- ↑ NASH, David H. Rotary engine geometry. Mathematics Magazine. March 1977, s. 87–89. doi:10.1080/0025570x.1977.11976621.; BADR, O.; NAIK, S.; O’CALLAGHAN, P. W.; PROBERT, S. D. Rotary Wankel engines as expansion devices in steam Rankine-cycle engines. Applied Energy. 1991, s. 59–76. doi:10.1016/0306-2619(91)90063-4..
- ↑ SNYDER, John P. Flattening the Earth: Two Thousand Years of Map Projections. [s.l.]: University of Chicago Press, 1997. Dostupné online. ISBN 978-0-226-76747-5. S. 40..
- ↑ KEUNING, Johannes. The history of geographical map projections until 1600. Imago Mundi. January 1955, s. 1–24. doi:10.1080/03085695508592085. JSTOR 1150090..
- ↑ a b BOWER, David I. The unusual projection for one of John Dee’s maps of 1580. The Cartographic Journal. February 2012, s. 55–61. Dostupné online. doi:10.1179/1743277411y.0000000015. S2CID 129873912..
- ↑ Fina Logo History: from Petrofina to Fina. Total: Group Presentation. Total S.A.. Dostupné v archivu pořízeném z originálu dne December 26, 2012..
- ↑ LINDLEY, Jeffrey A. Information: MUTCD — Interim Approval for the Optional Use of an Alternative Design for the U.S. Bicycle Route (M1-9) Sign (IA-15). Manual on Uniform Traffic Control Devices for Streets and Highways: Resources. US Department of Transportation, Federal Highway Administration, June 1, 2012. Dostupné online [cit. August 20, 2018].
Externí odkazy
 Obrázky, zvuky či videa k tématu Reuleauxův trojúhelník na Wikimedia Commons
Obrázky, zvuky či videa k tématu Reuleauxův trojúhelník na Wikimedia Commons
Média použitá na této stránce
Autor: LEMeZza, Licence: CC BY-SA 3.0
Reuleaux triangle inscribed in a square; bold black line shows the boundary of the shape, shadowed by rotating this triangle inside the square. This shape almost coincides with the square itself (what is used in drilling square holes), except for four corners, at each of which its boundary coincides with an arc of an ellipse. One of these four ellipses (red) is shown, and its center (the opposite vertex of the square) is marked.
Autor: David Eppstein, Licence: CC0
Parallel supporting lines of a Reuleaux triangle
Autor: LEMeZza, Licence: CC BY-SA 3.0
Reuleaux triangle inscribed in a square; the thin black line inside the square shows the boundary of the shape, shadowed by rotating this triangle inside the square. When the Reuleaux triangle rotates inside the square, its center moves along a closed curve (shown by bold black line) that is a union of four arcs of ellipses. One of these ellipses (red) is shows, with its center marked (red point).
Autor: LEMeZza, Licence: CC BY-SA 3.0
Reuleaux triangle shaped window of Onze-Lieve-Vrouwekerk, Bruges
Autor: LEMeZza, Licence: CC BY 3.0
Rotation of a Reuleaux triangle within a square, showing also the curve traced by the center of the triangle.
Mappamundi (World Map)
Autor: Stian Ellingsen, Licence: CC BY 2.5
Illustrates a Reuleaux tetrahedron and the four spheres that make it up by intersection. Made in Blender.
Autor: Frédéric MICHEL, Licence: CC BY-SA 3.0
How to build a w:Reuleaux triangle
The Reuleaux triangle is a constant width curve based on an equilateral triangle. The distances from any point on a side to the opposite vertex are all equal.