Riemannova hypotéza
Riemannova hypotéza (také Riemannova zeta-hypotéza) je jeden z nejslavnějších a nejdůležitějších nevyřešených problémů současné matematiky. Poprvé byla formulována německým matematikem Bernhardem Riemannem v roce 1859. Dokázáním Riemannovy hypotézy by bylo vyřešeno velké množství hlubokých problémů z různých oblastí matematiky (zejména teorie čísel), nejen proto byla v roce 2000 zařazena mezi 7 nejdůležitějších nevyřešených matematických problémů nového tisíciletí (problémy tisíciletí). Dne 24. září 2018 prohlásil sir Michael Atiyah, že ji vyřešil[1], ale jeho pokus o důkaz neobstál.[2] Za vyřešení je vypsána odměna 1 milion dolarů.
Matematická podstata
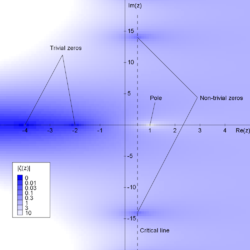
Riemannova hypotéza je domněnka o rozložení kořenů Riemannovy funkce zeta definované v celé komplexní rovině kromě bodu 1. Tato funkce má některé ze svých kořenů, triviální nulové body, v sudých záporných celých číslech. Kromě těchto kořenů existují ještě další, které se nazývají netriviální nulové body. Riemannova hypotéza je tvrzení:
- Všechny netriviální nulové body Riemannovy zeta-funkce mají reálnou část rovnu 1/2.
Čísla, jejichž reálná část je rovna 1/2, tvoří v komplexní rovině přímku, která se nazývá kritická přímka.
Nejsilnějšími známými částečnými řešeními Riemannovy hypotézy jsou různé verze věty o kritické přímce, které říkají, že na kritické přímce se vyskytuje „hodně“ netriviálních nulových bodů.
Netriviální nulové body
V roce 1900 byla s matematickou jistotou známa následující fakta o umístění netriviálních nulových bodů v komplexní rovině:
- Je jich nekonečně mnoho a všechny mají reálnou část mezi 0 a 1, přičemž krajní body vylučujeme.
Použijeme-li komplexní rovinu ke znázornění této situace, můžeme říci, že víme, že všechny netriviální nulové body leží v kritickém pásu. Riemannova hypotéza je však daleko silnější tvrzení - totiž že všechny leží na kritické přímce.
- Nulové body se objevují v komplexně sdružených dvojicích.
Jinými slovy, je-li nulový bod, je i nulový bod.
- Jejich reálné části jsou symetrické podle kritické přímky.
Tedy jestliže existuje nějaký nulový bod mimo kritickou přímku, pak jeho zrcadlový obraz podle kritické přímky je také nulovým bodem.
Odkazy
Reference
- ↑ POLESNÝ, David. Mám důkaz Riemannovy hypotézy, tvrdí britský matematik. Za vyřešení je odměna milion dolarů [online]. VTM, 2018-09-24 [cit. 2021-10-31]. Dostupné online.
- ↑ REHMEYER, Julie. Michael Atiyah, Mathematician in Newton’s Footsteps, Dies at 89 [online]. NY times, 2019-1-11 [cit. 2021-11-01]. Dostupné online. (angličtina)
Literatura
- John Derbyshire, Posedlost prvočísly, (2007) Academia, - Počet stran: 407.
- Bernhard Riemann, Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse, (1859) Monatsberichte der Berliner Akademie.
- Jacques Hadamard, Sur la distribution des zéros de la fonction ζ(s) et ses conséquences arithmétiques, Bulletin Société Mathématique de France 14 (1896) pp 199-220.
Související články
Externí odkazy
 Obrázky, zvuky či videa k tématu Riemannova hypotéza na Wikimedia Commons
Obrázky, zvuky či videa k tématu Riemannova hypotéza na Wikimedia Commons - (anglicky) (německy) Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse – původní Riemannův článek, v němž formuluje Riemannovu hypotézu
- Mirko Rokyta: Riemannova hypotéza – 160 let boje bez vítěze (video, MFF-FPF 7.10.2021)
Média použitá na této stránce
Autor: No machine-readable author provided. Conscious assumed (based on copyright claims)., Licence: CC BY-SA 3.0
Map of the Riemann zeta function absolute value.
