Rozdíl množin

Rozdíl množiny A (levý kruh) a množiny B (pravý kruh) :
${\displaystyle A\setminus B\;\;=\;\;A\cap B^{c}}$

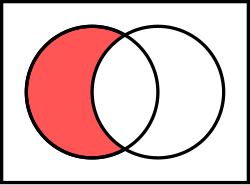
V matematice se jako rozdíl dvou množin označuje taková množina, která obsahuje každý prvek, který se nachází v první z množin, ale nenachází se ve druhé z nich, a žádné další prvky. Rozdíl množin A a B se označuje symbolem ${\displaystyle A-B}$, případně ${\displaystyle A\setminus B}$.

Formální definice

Pro všechna x platí, že ${\displaystyle x\in A-B\Leftrightarrow (x\in A\wedge x\not \in B)}$.

Příklad

• Rozdílem množin { 0, 2, 4, 6, 8, 10, 12, 14 } a { 0, 3, 6, 9, 12 } je množina { 2, 4, 8, 10, 14 }.
• Rozdílem množiny reálných čísel a racionálních čísel je množina iracionálních čísel.
• Rozdílem množiny celých čísel a nezáporných reálných čísel je množina všech záporných celých čísel.

Vlastnosti

Mějme libovolné množiny A, B a C. Potom platí následující rovnosti:

• C ∖ (A ∩ B) = (C ∖ A) ∪ (C ∖ B)
• C ∖ (A ∪ B) = (C ∖ A) ∩ (C ∖ B)
• C ∖ (B ∖ A) = (A ∩ C) ∪ (C ∖ B)
• (B ∖ A) ∩ C = (B ∩ C) ∖ A = B ∩ (C ∖ A)
• (B ∖ A) ∪ C = (B ∪ C) ∖ (A ∖ C)
• A ∖ A = ∅
• ∅ ∖ A = ∅
• A ∖ ∅ = A

Související články

• Množinové operace
• Průnik
• Sjednocení
• Doplněk množiny
• UNION